Two stones are through up simultaneously from the edge of a cliff 240 m high with initial speed of 10 m/s and 40 m/s respectively. Which of the following graphs best represents the time variation of relative position of the second stone with respect to the first? Assume stones do not rebound after hitting the ground and neglect air resistance, take . g=10m/s2 (The figures are schematic and not drawn to scale)
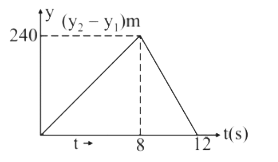
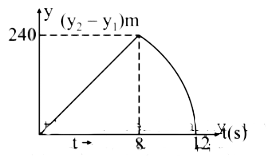

The correct Answer is:C
To solve the problem step by step, we need to analyze the motion of both stones and their relative positions over time.
Step 1: Understand the Initial Conditions
- Height of the cliff: 240 m
- Initial speed of Stone 1 (S1): 10 m/s (upwards)
- Initial speed of Stone 2 (S2): 40 m/s (upwards)
- Acceleration due to gravity (g): 10 m/s² (downwards)
Step 2: Determine the Time of Flight for Each Stone
To find out how long each stone takes to hit the ground, we can use the kinematic equation:
h=vit+12at2
Where:
- h = height (240 m)
- vi = initial velocity
- a = acceleration (which is -g because it acts downwards)
For Stone 1 (S1):
240=10t−12(10)t2
240=10t−5t2
5t2−10t+240=0
Using the quadratic formula t=−b±√b2−4ac2a:
Here, a=5,b=−10,c=240:
t=10±√(−10)2−4⋅5⋅2402⋅5
t=10±√100−480010
Since the discriminant is negative, Stone 1 will hit the ground before reaching the maximum height.
For Stone 2 (S2):
240=40t−12(10)t2
240=40t−5t2
5t2−40t+240=0
Using the quadratic formula again:
Here, a=5,b=−40,c=240:
t=40±√(−40)2−4⋅5⋅2402⋅5
t=40±√1600−480010
Again, the discriminant is negative, indicating that Stone 2 will also hit the ground.
Step 3: Analyze Relative Motion
The relative velocity between the two stones is:
vrel=vS2−vS1=40−10=30 m/s
This means that Stone 2 is moving away from Stone 1 at a constant rate of 30 m/s until one of them hits the ground.
Step 4: Determine the Position Function
The position of each stone can be described by:
- For Stone 1:
y1(t)=240+10t−5t2
- For Stone 2:
y2(t)=240+40t−5t2
Step 5: Find the Relative Position
The relative position of Stone 2 with respect to Stone 1 is given by:
yrel(t)=y2(t)−y1(t)
yrel(t)=(240+40t−5t2)−(240+10t−5t2)
yrel(t)=30t
Step 6: Determine the Graph Behavior
- For the time before both stones hit the ground, the relative position increases linearly with a slope of 30.
- After Stone 1 hits the ground, it stops moving, and Stone 2 continues to fall under gravity, which means the relative position will start to decrease as Stone 2 falls.
Conclusion
The graph of the relative position of Stone 2 with respect to Stone 1 will show a linear increase until Stone 1 hits the ground, followed by a curve that decreases as Stone 2 falls.
- Height of the cliff: 240 m
- Initial speed of Stone 1 (S1): 10 m/s (upwards)
- Initial speed of Stone 2 (S2): 40 m/s (upwards)
- Acceleration due to gravity (g): 10 m/s² (downwards)
To find out how long each stone takes to hit the ground, we can use the kinematic equation:
h=vit+12at2
Where:
- h = height (240 m)
- vi = initial velocity
- a = acceleration (which is -g because it acts downwards)
240=10t−12(10)t2
240=10t−5t2
5t2−10t+240=0
Using the quadratic formula t=−b±√b2−4ac2a:
Here, a=5,b=−10,c=240:
t=10±√(−10)2−4⋅5⋅2402⋅5
t=10±√100−480010
Since the discriminant is negative, Stone 1 will hit the ground before reaching the maximum height.
240=40t−12(10)t2
240=40t−5t2
5t2−40t+240=0
Using the quadratic formula again:
Here, a=5,b=−40,c=240:
t=40±√(−40)2−4⋅5⋅2402⋅5
t=40±√1600−480010
Again, the discriminant is negative, indicating that Stone 2 will also hit the ground.
The relative velocity between the two stones is:
vrel=vS2−vS1=40−10=30 m/s
This means that Stone 2 is moving away from Stone 1 at a constant rate of 30 m/s until one of them hits the ground.
The position of each stone can be described by:
- For Stone 1:
y1(t)=240+10t−5t2
- For Stone 2:
y2(t)=240+40t−5t2
The relative position of Stone 2 with respect to Stone 1 is given by:
yrel(t)=y2(t)−y1(t)
yrel(t)=(240+40t−5t2)−(240+10t−5t2)
yrel(t)=30t
- For the time before both stones hit the ground, the relative position increases linearly with a slope of 30.
- After Stone 1 hits the ground, it stops moving, and Stone 2 continues to fall under gravity, which means the relative position will start to decrease as Stone 2 falls.
The graph of the relative position of Stone 2 with respect to Stone 1 will show a linear increase until Stone 1 hits the ground, followed by a curve that decreases as Stone 2 falls.
Topper's Solved these Questions
- KINEMATICS OF A PARTICLE BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - JEE Advanced (archive)
14 Videos
- KINEMATICS OF A PARTICLE BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - LEVEL 2
65 Videos
- JEE MAIN REVISON TEST-23BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISON TEST-23EXERCISE - PHYSICS (SECTION 2)
1 Videos
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE
53 Videos
Similar Questions
Two stones are thrown up simultaneously from the edge of a cliff with initial speed vand2v. The relative position of the second stone with respect to first varies with time till both the stones strike the ground as.
View SolutionOne stone is projected horizontally from a 20m high cliff with an initial speed of 10ms−1. A second stone is simultaneously dropped from that cliff. Which of the following is true?
View Solution
Knowledge Check
Two stones are thrown up simultaneously from the edge of a cliff 200 m high with initial speeds of 15ms−1 and 30ms−1 respectively. The time variation of the relative position of the second stone with respect to the first is shown in the figure. The equation of the linear part is
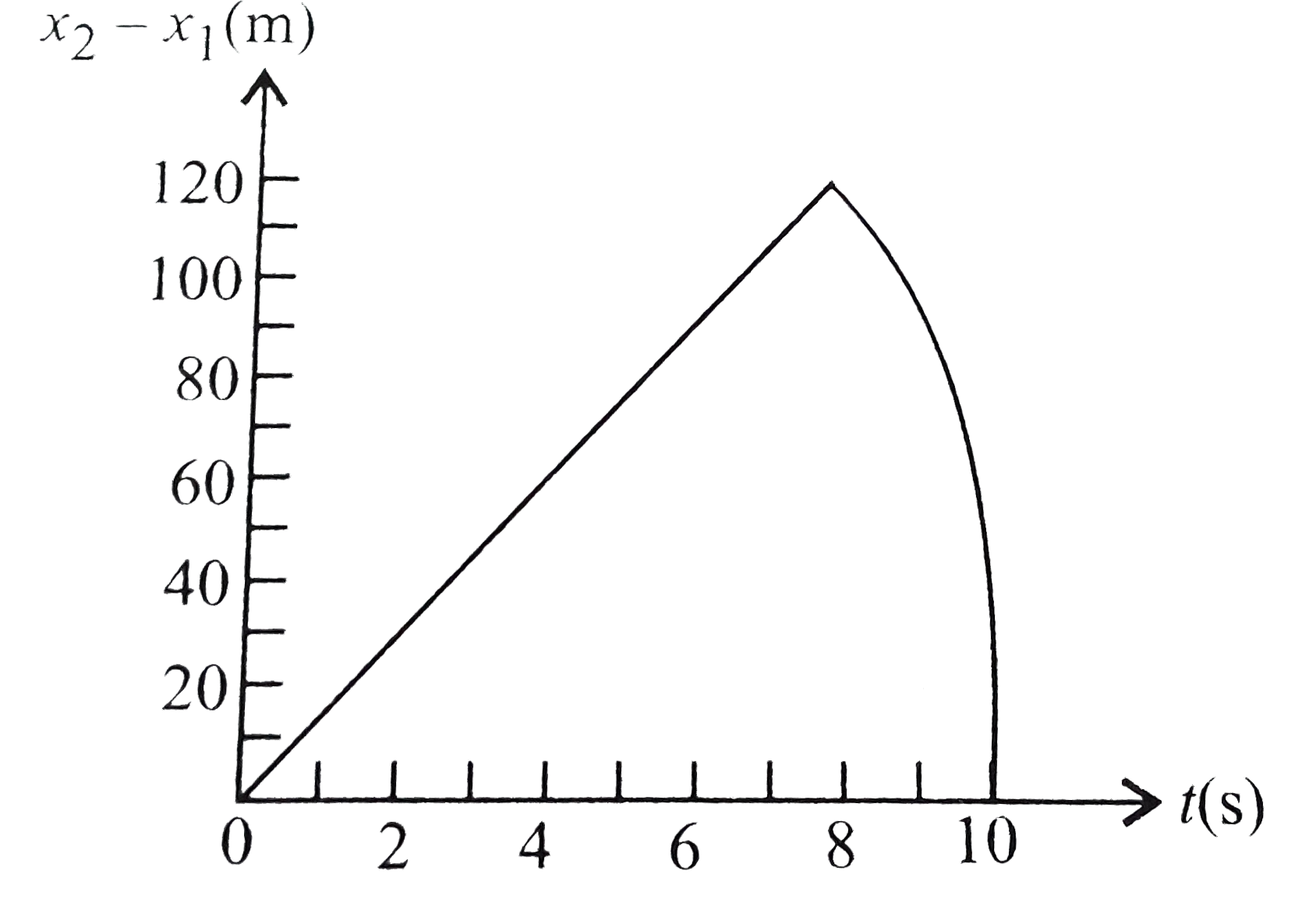 Ax2−x1 = 50tBx2−x1 = 10tCx2−x1 = 15tDx2−x1 = 20t
Ax2−x1 = 50tBx2−x1 = 10tCx2−x1 = 15tDx2−x1 = 20t
Two stones are thrown vertically upwards simultaneously from the same point on the ground with initial speed u1=30m/sec and u2=50m/sec. Which of the curve represent correct variation (for the time interval in which both reach the ground) of
(x2−x1) = the relative position of second stone with respect to first with time (t)
(v2−v1) = the relative velocity of second stone with respect to first with time (t).
Assuming that stones do not rebound after hitting.
View SolutionTwo stones AandB are projected simultaneously from the top of a 100−m high tower. Stone B is projected horizontally with speed 10ms−1, and stone A is droppd from the tower. Find out the following :
(a) Time of flight of the two stone
(b) Distance between two stones after 3s
(c ) Angle of strike with ground
(d) Horizontal range of particle B.
View SolutionA man standing on the edge of a cliff throws a stone straight up with initial speed (u) and then throws another stone straight down with same initial speed and from the same position. Find the ratio of the speeds. The stones would have attained when they hit ground at the base of the cliff.
View SolutionA stone released with zero velocity from the top of a tower, reaches the ground in 4s. The height of the tower is (g=10m/s2)
View SolutionA ball is thrown upwards from the top of a tower 40m high with a velocity of 10m/s. Find the time when it strikes the ground. Take g=10m/s2.
View SolutionA ball is thrown upwards from the top of a tower 40m high with a velocity of 10m/s. Find the time when it strikes the ground. Take g=10m/s2.
View SolutionA stone is thrown vertically upward with a speed of 10.0ms−1 from the edge of a cliff 65 m high. What will be its speed just before hitting the bottom ?
View Solution
