The dependence of acceleration due to gravity g on the distance r from the centre of the earth assumed to be a sphere of radius R of uniform density is as shown figure below.
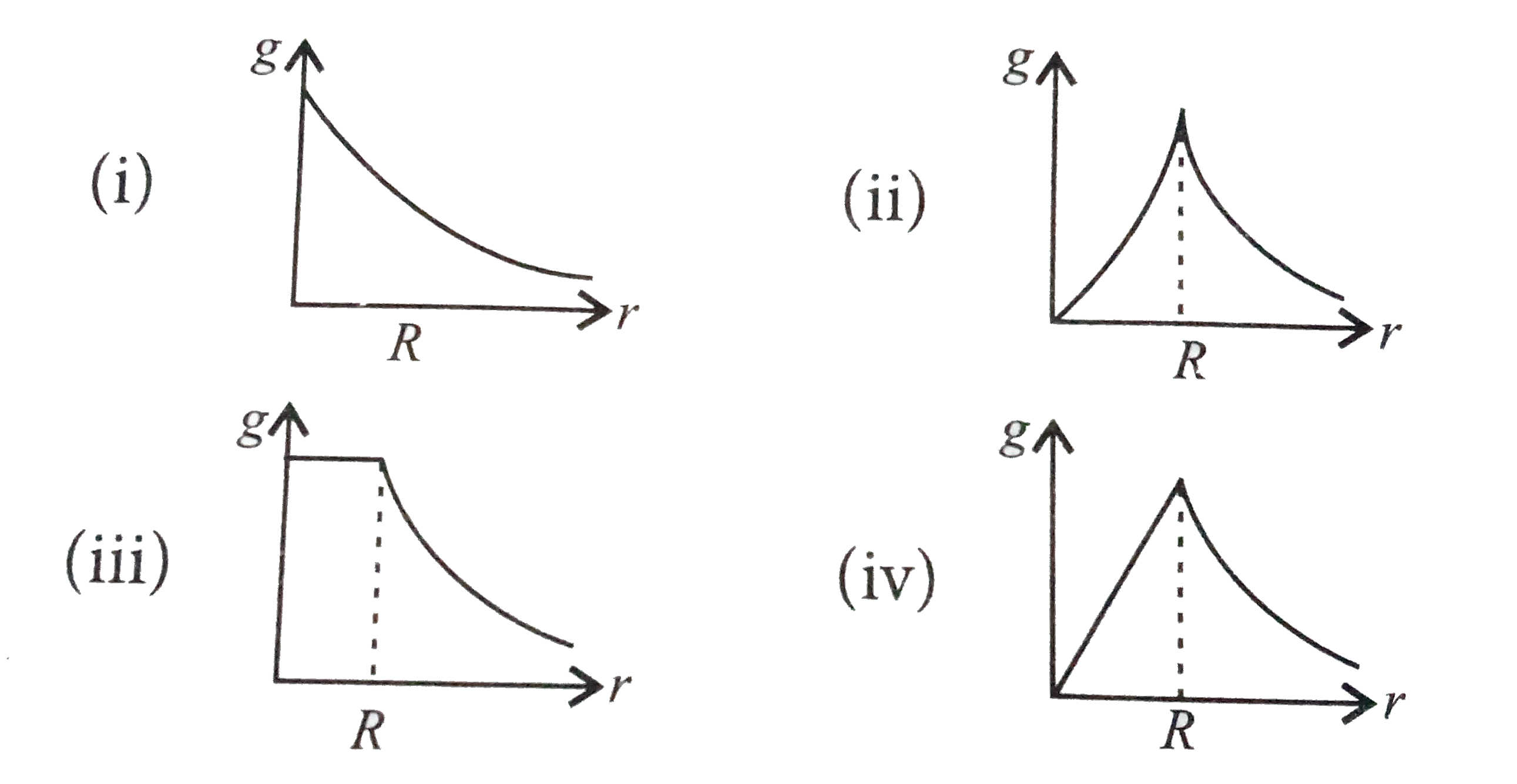
The correct figure is
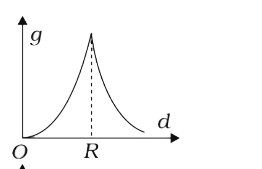
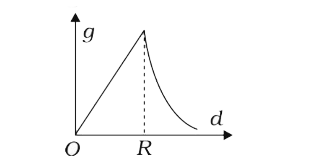
The correct Answer is:D
For point P earth
g=GMR3×r o < r≤R
For point P outside the earth
g=GMr2r≥R
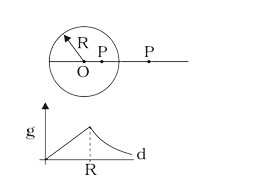
Topper's Solved these Questions
- GRAVITATIONBook:VMC MODULES ENGLISHChapter:GRAVITATIONExercise:JEE Advance (Archive) SINGLE OPTION CORRECT
Explore 14 Videos
- GRAVITATIONBook:VMC MODULES ENGLISHChapter:GRAVITATIONExercise:JEE Advance (Archive) MULTIPLE OPTIONS CORRECT TYPE
Explore 5 Videos
- GRAVITATIONBook:VMC MODULES ENGLISHChapter:GRAVITATIONExercise:Level-2
Explore 30 Videos
- GASEOUS STATE & THERMODYNAMICSBook:VMC MODULES ENGLISHChapter:GASEOUS STATE & THERMODYNAMICSExercise:JEE ADVANCED (ARCHIVE )
Explore 111 Videos
- INTRODUCTION TO VECTORS & FORCES Book:VMC MODULES ENGLISHChapter:INTRODUCTION TO VECTORS & FORCES Exercise:JEE Advanced ( ARCHIVE LEVEL-2)
Explore 12 Videos
Similar Questions
The acceleration due to gravity at a depth R/2 below the surface of the earth is
View SolutionThe value of g (acceleration due to gravity) at earth's surface is 10ms−2. Its value in ms−2 at the centre of the earth which is assumed to be a sphere of radius R metre and uniform mass density is
View Solution
Knowledge Check
The dependence of acceleration due to gravity g on the distance r from the centre of the earth, assumed to be a sphere of radius R of uniform density is as shown in Fig. below:
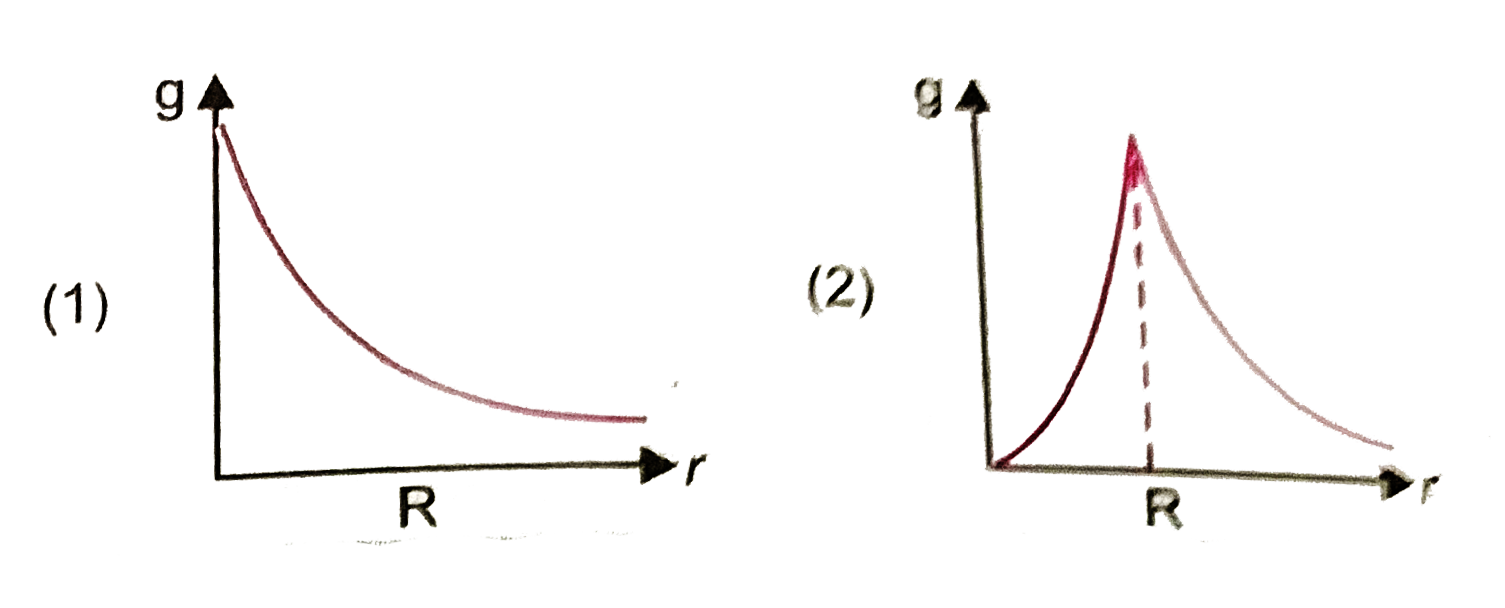
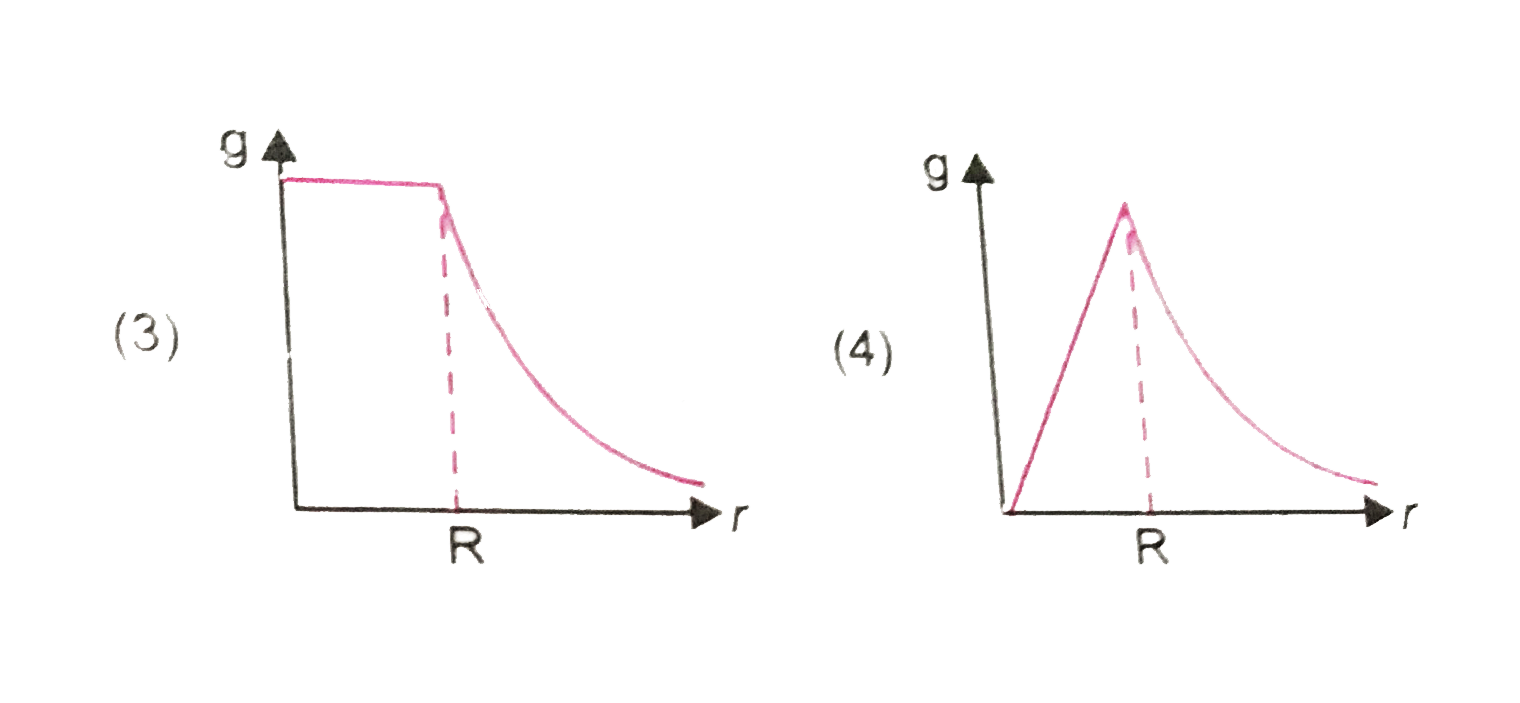
The correct figure isA(i)B(ii)C(iii)D(iv)
Assuming the earth to be a sphere of uniform density, the acceleration due to gravity
View SolutionFigure shows variation of acceleration due to gravity with distance from centre of a uniform spherical planet, Radius of planet is R. What is r1−r1
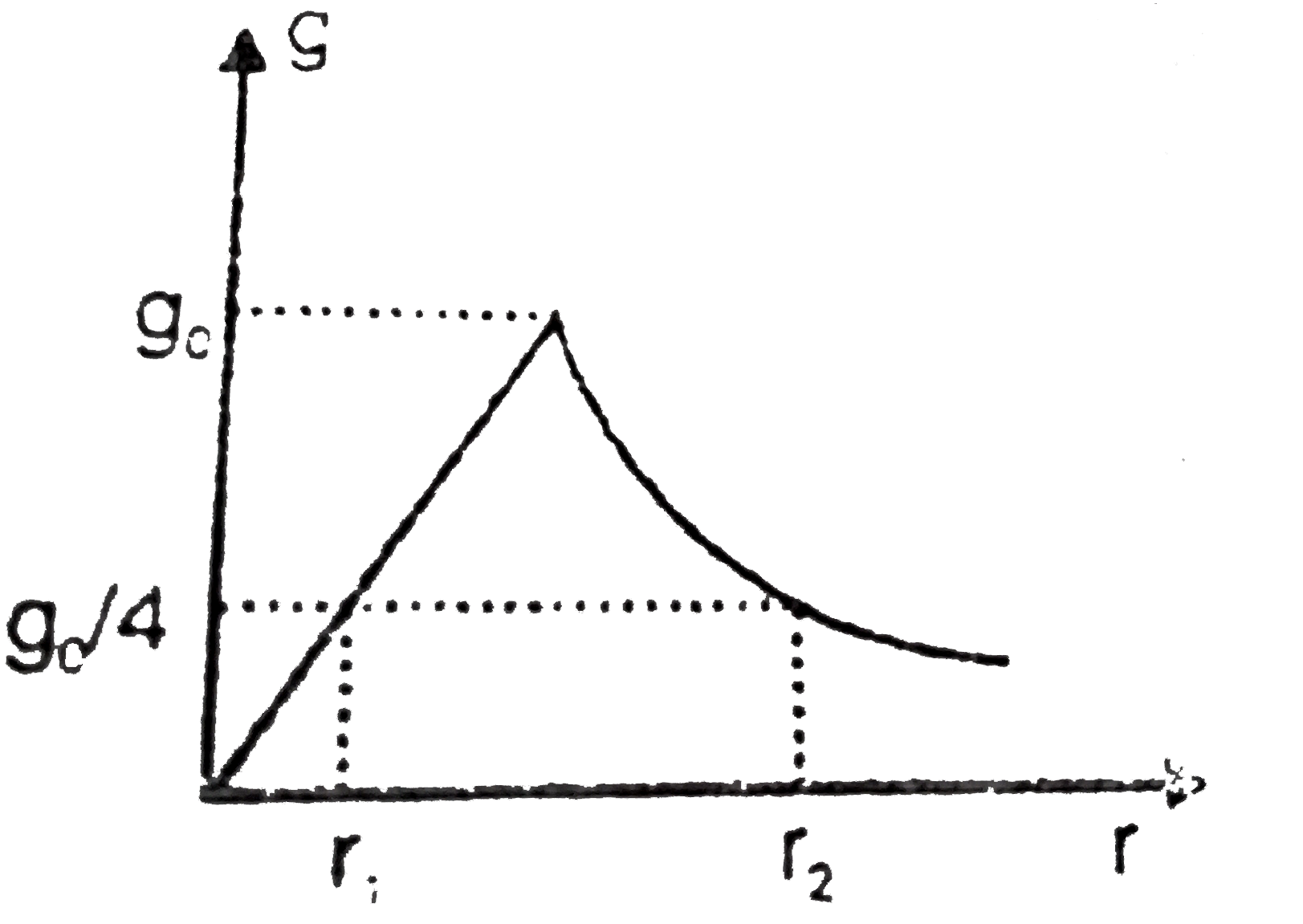
View SolutionIf acceleration due to gravity at distance d [<R] from the centre of earth is β , then its value at distance d above the surface of earth will be [ where R is radius of earth ]
View SolutionWhat will be the acceleration due to gravity at a distance of 3200 km below the surface of the earth ? (Take Re=6400 km)
View SolutionA point charge q , is placed at a distance r from the centre of an aluminium sphere, of radius R (r>R) . Selectr the correct alternatives.
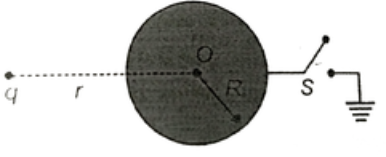
View SolutionStarting from the centre of the earth having radius R, the variation of g (acceleration due to gravity) is shown by
View SolutionIf R is the radius of the earth and g the acceleration due to gravity on the earth's surface, the mean density of the earth is
View Solution

