A solid sphere of radius a and mass m is surrounded by cocentric spherical shell of thickness 2a and mass 2m the gravitational field at a distance 3a from their centres is
GM9a2
2GM9a2
GM3a2
2Gm3a2
The correct Answer is:C
Ep=GM(3a)2+G2M(3a)2+GM3a2
Topper's Solved these Questions
- GRAVITATIONBOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - JEE Advance (Archive) SINGLE OPTION CORRECT
14 Videos
- GRAVITATIONBOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - JEE Advance (Archive) MULTIPLE OPTIONS CORRECT TYPE
5 Videos
- GRAVITATIONBOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - Level-2
30 Videos
- GASEOUS STATE & THERMODYNAMICSBOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - JEE ADVANCED (ARCHIVE )
111 Videos
- INTRODUCTION TO VECTORS & FORCES BOOK - VMC MODULES ENGLISHCHAPTER - INTRODUCTION TO VECTORS & FORCES EXERCISE - JEE Advanced ( ARCHIVE LEVEL-2)
12 Videos
Similar Questions
A solid sphere of mass 'M' and radius 'a' is surrounded by a uniform concentric spherical shell of thickness 2a and mass 2M. The gravitational field at distance '3a' from the centre will be :
View SolutionA uniform solid sphere of mass M and radius a is surrounded symmetrically by a uniform thin spherical shell of equal mass and radius 2a. Find the gravitational field at a distance a). 3/2 a from the centre , b). 5/2 as from the centre.
View SolutionA uniform solid sphere of mass M and radius a is surrounded symmetrically by a uniform thin spherical shell of equal mass and radius 2a.Find the gravitational field at a distance a. 32a from the center , b. 52a from the center.
View SolutionA uniform sphere of mass M and radius R is surrounded by a concentric spherical shell of same mass but radius 2R. A point mass is kept at a distance x(>R) in the region bounded by spheres as shown in the figure . The net gravitational force on the particle is

View SolutionA uniform metal sphere of radius R and mass m is surrounded by a thin uniform spherical shell of same mass and radius 4R. The centre of the shell C falls on the surface of the inner sphere. Find the gravitational fields at points A and B.

View SolutionA particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a2 from the centre.
View SolutionA particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a2 from the centre.
View SolutionA uniform solid sphere of mass m and radius r is suspended symmetrically by a uniform thin spherical shell of radius 2r and mass m.
View SolutionA uniform metal sphere of radius a and mass M is surrounded by a thin uniform spherical shell of equal mass and redius 4a. The centre of the shell falls on the surface of the iner sphere
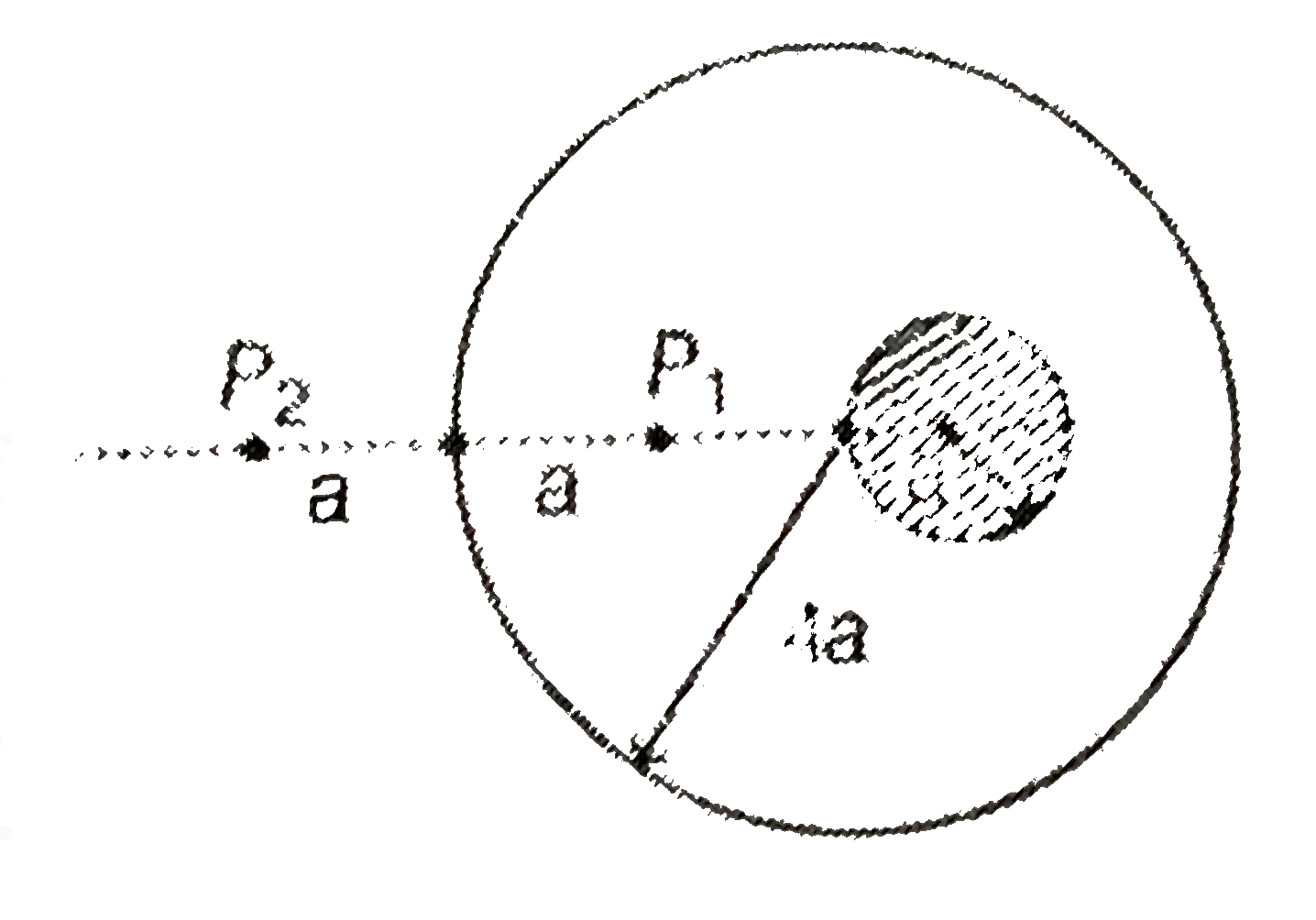
View SolutionA body of mass m is placed at the centre of the spherical shell of radius R and mass M. The gravitation potential on the surface of the shell is
View Solution
