The mass density of a spherical body is given by ρ(r)=kr for r≤R and ρ(r)=0for r > R , where r is the distance from the centre. The correct graph that describes qualitatively the acceleration, a, of a test particle as a function of r is :
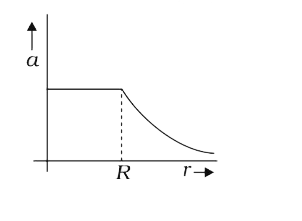
The correct Answer is:B
To solve the problem, we need to analyze the given mass density function and determine how it affects the gravitational acceleration of a test particle as a function of the distance r from the center of the spherical body.
1. Understanding the Mass Density:
The mass density of the spherical body is given by:
ρ(r)=krfor r≤R
and
ρ(r)=0for r>R
Here, k is a constant, and R is the radius of the sphere.
2. Finding the Mass of a Shell:
To find the mass of a thin spherical shell of thickness dr at a distance r from the center, we use the formula for the volume of the shell:
dV=4πr2dr
The mass of this shell is:
dm=ρ(r)⋅dV=kr⋅4πr2dr=4πkrdr
3. Calculating the Total Mass Inside Radius r:
To find the total mass M(r) inside a radius r, we integrate the mass of the shell from 0 to r:
M(r)=∫r04πkr′dr′=4πk∫r0r′dr′=4πk((r′)22)r0=4πkr22=2πkr2
4. Finding the Gravitational Field g(r):
The gravitational field g(r) at a distance r from the center is given by:
g(r)=GM(r)r2
Substituting M(r):
g(r)=G(2πkr2)r2=2πGk
This shows that g(r) is constant for r≤R.
5. Behavior for r>R:
For r>R, the mass inside the sphere is constant (equal to M(R)). Thus, the gravitational field becomes:
g(r)=GM(R)r2
Since M(R)=2πkR2, we have:
g(r)=G(2πkR2)r2
This indicates that g(r) decreases with r2 for r>R.
6. Conclusion:
- For r≤R, g(r) is constant.
- For r>R, g(r) decreases as 1r2.
Correct Graph:
The graph of the gravitational acceleration g(r) as a function of r will be constant for r≤R and will decrease for r>R. Thus, the correct option is the one that shows a constant value for g up to R and a decreasing curve after R.
The mass density of the spherical body is given by:
ρ(r)=krfor r≤R
and
ρ(r)=0for r>R
Here, k is a constant, and R is the radius of the sphere.
To find the mass of a thin spherical shell of thickness dr at a distance r from the center, we use the formula for the volume of the shell:
dV=4πr2dr
The mass of this shell is:
dm=ρ(r)⋅dV=kr⋅4πr2dr=4πkrdr
To find the total mass M(r) inside a radius r, we integrate the mass of the shell from 0 to r:
M(r)=∫r04πkr′dr′=4πk∫r0r′dr′=4πk((r′)22)r0=4πkr22=2πkr2
The gravitational field g(r) at a distance r from the center is given by:
g(r)=GM(r)r2
Substituting M(r):
g(r)=G(2πkr2)r2=2πGk
This shows that g(r) is constant for r≤R.
For r>R, the mass inside the sphere is constant (equal to M(R)). Thus, the gravitational field becomes:
g(r)=GM(R)r2
Since M(R)=2πkR2, we have:
g(r)=G(2πkR2)r2
This indicates that g(r) decreases with r2 for r>R.
- For r≤R, g(r) is constant.
- For r>R, g(r) decreases as 1r2.
The graph of the gravitational acceleration g(r) as a function of r will be constant for r≤R and will decrease for r>R. Thus, the correct option is the one that shows a constant value for g up to R and a decreasing curve after R.
Topper's Solved these Questions
- GRAVITATIONBook:VMC MODULES ENGLISHChapter:GRAVITATIONExercise:JEE Advance (Archive) SINGLE OPTION CORRECT
Explore 14 Videos
- GRAVITATIONBook:VMC MODULES ENGLISHChapter:GRAVITATIONExercise:JEE Advance (Archive) MULTIPLE OPTIONS CORRECT TYPE
Explore 5 Videos
- GRAVITATIONBook:VMC MODULES ENGLISHChapter:GRAVITATIONExercise:Level-2
Explore 30 Videos
- GASEOUS STATE & THERMODYNAMICSBook:VMC MODULES ENGLISHChapter:GASEOUS STATE & THERMODYNAMICSExercise:JEE ADVANCED (ARCHIVE )
Explore 111 Videos
- INTRODUCTION TO VECTORS & FORCES Book:VMC MODULES ENGLISHChapter:INTRODUCTION TO VECTORS & FORCES Exercise:JEE Advanced ( ARCHIVE LEVEL-2)
Explore 12 Videos
Similar Questions
Find the gravitational potential due to a spherical shell of mass M and radius R at r<R and r>R, where r is the distance from the centre of the shell.
View SolutionLet there be a spherical symmetric charge density varying as p(r)=p0rR upto r = R and ρ(r)=0 for r>R, where r is the distance from the origin. The electric field at on a distance r(r<R) from the origin is given by -
View SolutionThe density inside a solid sphere of radius a is given by ρ=ρ0r, where ρ0 is the density at the surface and r denotes the distance from the centre. Find the gravitational field due to this sphere at a distance 2a from its centre.
View SolutionThe potential energy function of a particle is given by U(r)=A2r2−B3r, where A and B are constant and r is the radial distance from the centre of the force. Choose the correct option (s)
View SolutionLet there be a spherically symmetric charge distribution with charge density varying as ρ(r)=ρ(54−rR) upto r=R, and ρ(r)=0 for r>R, where r is the distance from the origin. The electric field at a distance r(rltR) from the origin is given by
View SolutionThe density inside a solid sphere of radius a is given by ρ=ρ0r, where ρ0 is the density ast the surface and r denotes the distance from the centre. Find the graittional field due to this sphere at a distance 2a from its centre.
View SolutionThe mass density of a spherical galaxy varies as Kr over a large distance 'r' from its centre . In that region , a small star is in a circular orbit of radius R . Then the period of revolution , T depends on R as :
View SolutionCharge density of a sphere of radius R is ρ=ρ0r where r is distance from centre of sphere.Total charge of sphere will be

View SolutionLet a total charge 2Q be distributed in a sphere of radius R, with the charge density given by , ρ(r)=kr, where r is the distance from the centre. Two charge A and B, of –Q each, are placed on diametrically opposite points, at equal distance, a from the centre. If A and B do not experience any force, then:
View SolutionThe potential energy of a particle in a force field is:
U=Ar2−Br,. Where A and B are positive
constants and r is the distance of particle from the centre of the field. For stable equilibrium the distance of the particle is
View Solution

