The minimum acceleration with which a fireman can slide down a rope of breaking strength two - third of his weight is
The correct Answer is:0.33
To solve the problem of finding the minimum acceleration with which a fireman can slide down a rope of breaking strength two-thirds of his weight, we can follow these steps:
1. Identify the Forces Acting on the Fireman:
- The fireman has a weight W=mg acting downwards (where m is the mass of the fireman and g is the acceleration due to gravity).
- The tension T in the rope acts upwards.
2. Set Up the Equation of Motion:
- When the fireman slides down with an acceleration a, the net force acting on him can be expressed using Newton's second law:
mg−T=ma
3. Determine the Maximum Tension:
- The breaking strength of the rope is given as two-thirds of the fireman's weight:
T=23mg
4. Substitute the Tension into the Equation:
- Replace T in the equation of motion with 23mg:
mg−23mg=ma
5. Simplify the Equation:
- Factor out mg:
mg(1−23)=ma
- This simplifies to:
mg(13)=ma
6. Cancel the Mass m (assuming m≠0):
- Dividing both sides by m:
g(13)=a
7. Final Expression for Acceleration:
- Thus, the minimum acceleration a is:
a=g3
Conclusion:
The minimum acceleration with which the fireman can slide down the rope is g3.
- The fireman has a weight W=mg acting downwards (where m is the mass of the fireman and g is the acceleration due to gravity).
- The tension T in the rope acts upwards.
- When the fireman slides down with an acceleration a, the net force acting on him can be expressed using Newton's second law:
mg−T=ma
- The breaking strength of the rope is given as two-thirds of the fireman's weight:
T=23mg
- Replace T in the equation of motion with 23mg:
mg−23mg=ma
- Factor out mg:
mg(1−23)=ma
- This simplifies to:
mg(13)=ma
- Dividing both sides by m:
g(13)=a
- Thus, the minimum acceleration a is:
a=g3
The minimum acceleration with which the fireman can slide down the rope is g3.
Topper's Solved these Questions
- DYNAMICS OF A PARTICLEBOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - JEE Main (Archive) Level - I
29 Videos
- DYNAMICS OF A PARTICLEBOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - JEE Advance (Archive) Level - II (SINGLE OPTION CORRECT TYPE )
31 Videos
- DYNAMICS OF A PARTICLEBOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - LEVEL 2
49 Videos
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - JEE ADVANCED ARCHIVE
68 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - IN-CHAPTER EXERCISE-G
10 Videos
Similar Questions
Knowledge Check
With what minimum acceleration can a fireman slide down a rope whose breaking strength is (2/3) of his weight?
Ag2B23gC32gDg3
At what minimum acceleration should a monkey slide a rope whose breaking strength is 23rd of its weight?
View SolutionThe minimum value of acceleration of wedge for which the block start sliding on the wedge, is:
View SolutionA rope of negligible mass passes over a pulley of negligible mass attached to the ceiling, as shown in figure. One end of the rope is held by Student A of mass 70kg, who is at rest on the floor. The opposite end of the rope is held by Student B of mass 60kg, who is suspended at rest above the floor. The minimum acceleration a0 with which the Student B should climb up the rope to lift the Student A upward off the floor. (g=10m/s2)
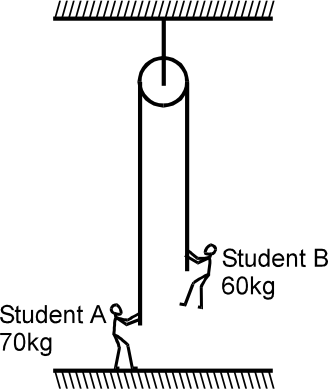
View SolutionA rope of negligible mass passes over a pulley of negligible mass attached to the ceiling, as shown in figure. One end of the rope is held by Student A of mass 70kg, who is at rest on the floor. The opposite end of the rope is held by Student B of mass 60kg, who is suspended at rest above the floor. The minimum acceleration a0 with which the Student B should climb up the rope to lift the Student A upward off the floor. (g=10m/s2)

View SolutionA monkey is descending from the branch of a tree with a constant acceleration. If the breaking strength of the branch is 75% of the weight of the monkey, the minimum acceleration with which the monkey can slide down without breaking the branch is
View SolutionA body of mass 60 kg is holding a vertical rope . The rope can break when a mass of 75 kg is suspended from it. The maximum acceleration with which the boy can climb the rope without breaking it is :(g=10m/s2)
View SolutionA body of mass 50 kg and specific gravity force is to be lifted using a rope of breaking strength of 60 kg wt. The acceleration with which it can be pulled up in least interval of time
View Solution
