A coin is placed at the edge of a horizontal disc rotating about a vertical axis through its axis with a uniform angular speed 2 rad s−1. The radius of the disc is 50 cm. Find the minimum coefficient of friction between disc and coin so that the coin does not slip. (Take g=10m/s2)
The correct Answer is:0.2
To solve the problem, we need to determine the minimum coefficient of friction (μ) required to prevent the coin from slipping off the rotating disc. Here’s a step-by-step solution:
Step 1: Identify the given values
- Angular speed (ω) = 2 rad/s
- Radius of the disc (R) = 50 cm = 0.5 m (convert to meters)
- Acceleration due to gravity (g) = 10 m/s²
Step 2: Calculate the centrifugal force acting on the coin
The centrifugal force (Fc) acting on the coin can be calculated using the formula:
Fc=m⋅ω2⋅R
Substituting the values:
Fc=m⋅(2)2⋅(0.5)
Fc=m⋅4⋅0.5
Fc=2m
Step 3: Identify the forces acting on the coin
The forces acting on the coin include:
- The gravitational force (weight) acting downwards: Fg=mg
- The normal force (N) acting upwards: N=mg
- The frictional force (Ff) acting towards the center of the disc: Ff=μN
Step 4: Set up the equilibrium condition
For the coin to not slip, the frictional force must be equal to the centrifugal force:
Ff=Fc
Substituting the expressions for frictional force and centrifugal force:
μN=Fc
Since N=mg, we can substitute this into the equation:
μ(mg)=2m
Step 5: Simplify the equation
We can cancel the mass (m) from both sides (assuming m ≠ 0):
μg=2
Now substituting the value of g:
μ(10)=2
Step 6: Solve for the coefficient of friction (μ)
Now, we can solve for μ:
μ=210
μ=0.2
Conclusion
The minimum coefficient of friction required to prevent the coin from slipping off the disc is:
μ=0.2
---
- Angular speed (ω) = 2 rad/s
- Radius of the disc (R) = 50 cm = 0.5 m (convert to meters)
- Acceleration due to gravity (g) = 10 m/s²
The centrifugal force (Fc) acting on the coin can be calculated using the formula:
Fc=m⋅ω2⋅R
Substituting the values:
Fc=m⋅(2)2⋅(0.5)
Fc=m⋅4⋅0.5
Fc=2m
The forces acting on the coin include:
- The gravitational force (weight) acting downwards: Fg=mg
- The normal force (N) acting upwards: N=mg
- The frictional force (Ff) acting towards the center of the disc: Ff=μN
For the coin to not slip, the frictional force must be equal to the centrifugal force:
Ff=Fc
Substituting the expressions for frictional force and centrifugal force:
μN=Fc
Since N=mg, we can substitute this into the equation:
μ(mg)=2m
We can cancel the mass (m) from both sides (assuming m ≠ 0):
μg=2
Now substituting the value of g:
μ(10)=2
Now, we can solve for μ:
μ=210
μ=0.2
The minimum coefficient of friction required to prevent the coin from slipping off the disc is:
μ=0.2
Topper's Solved these Questions
- DYNAMICS OF A PARTICLEBOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - JEE Main (Archive) Level - I
29 Videos
- DYNAMICS OF A PARTICLEBOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - JEE Advance (Archive) Level - II (SINGLE OPTION CORRECT TYPE )
31 Videos
- DYNAMICS OF A PARTICLEBOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - LEVEL 2
49 Videos
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - JEE ADVANCED ARCHIVE
68 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - IN-CHAPTER EXERCISE-G
10 Videos
Similar Questions
A horizontal disc is rotating about a vertical axis passing through its centre. If an insect moves from centre to rim then the angular momentum of the system
View SolutionA block of mass 1kg is placed on the periphery of a rotating rough circular table of radius 50cm as shown in the figure.Angular velocity of the table is 4 rad/s.The minimum value of coefficient of friction between the contact such that there is no relative slipping is (g=10ms2)
_PHY_E05_167_Q01.png)
View SolutionA point at the periphery of a disc rotating about a fixed axis moves so that its speed varies with time as v=2t2m/s The tangential acceleration of the point at t= 1s is
View SolutionA disc of radius 10 cm is rotating about its axis at an angular speed of 20 rad/s. Find the linear speed of
a. a point on the rim,
b. the middle point of the radius.
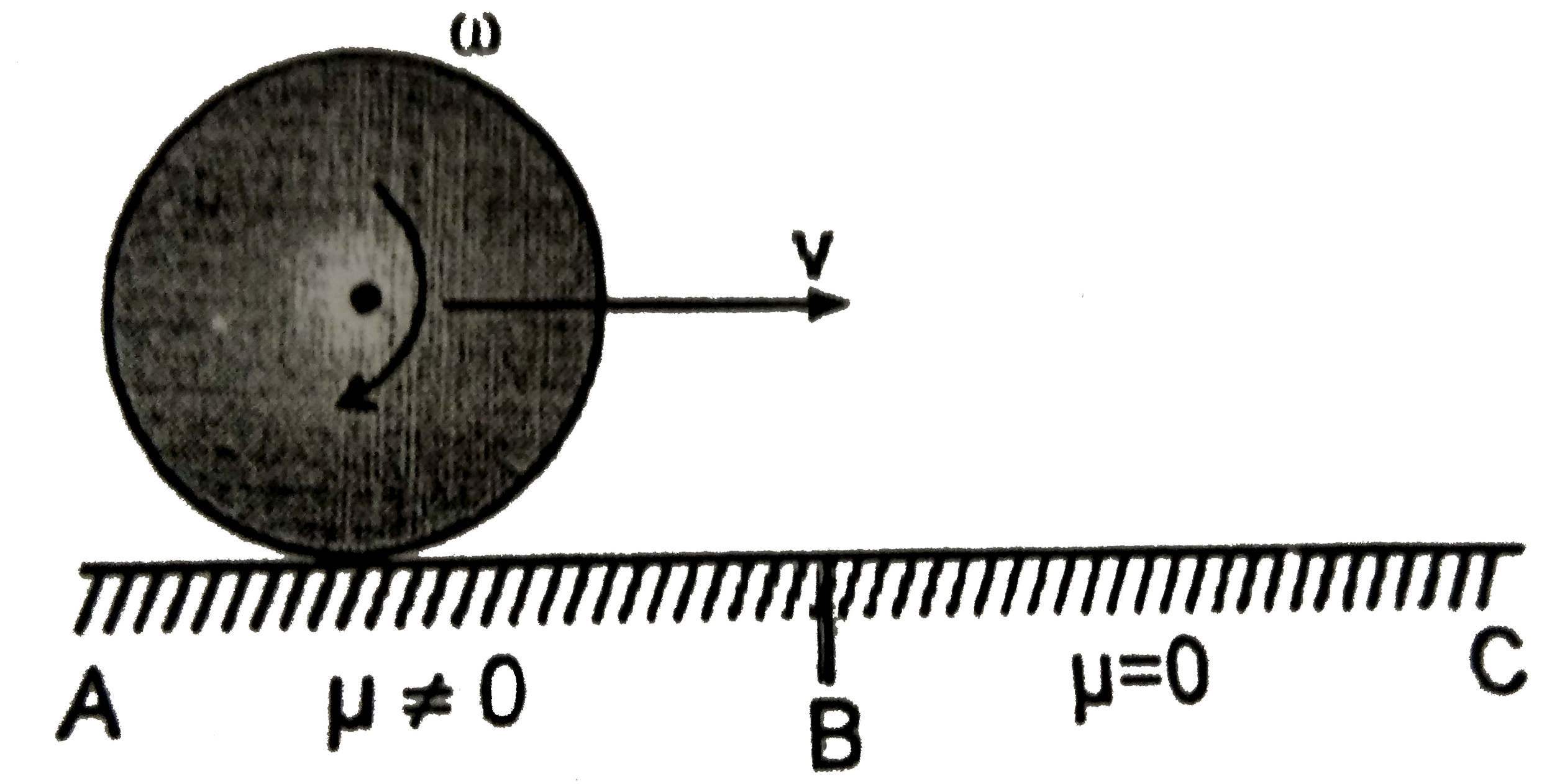
View SolutionAs shown in the figure, a disc of mass m is rolling without slipping a angular velocity ω. When it crosses point B disc will be in :
View SolutionA disc rotating about its axis, from rest it acquires a angular speed 100rev/s in 4 second. The angle rotated by it during these seconds (in radian ) is :-
View SolutionA small coin of mass 40 g is placed on the horizontal surface of a rotating disc. The disc starts from rest and is given a constant angular acceleration α=2 rad s−2. The coefficient of static friction between the coin and the disc is μs=3/4 and the coefficient of kinetic friction is μk=0.5. The coin is placed at a distance r=1m from the centre of the disc. The magnitude of the resultant force on the coin exerted by the disc just before it starts slipping on the disc is?

View SolutionA circular disc is made to rotate in horizontal plane about its centre at the rate of 2 rps. The greatest distance of a coin placed on the disc from its centre so that it does not skid is (μ is coefficient of friction)
View SolutionA disc starts rotating with a constant angular acceleration of 1rad/s2 about a fixed vertical axis perpendicular to its plane and passing through its centre. A coin of mass 10gm is placed on the disc at a distance of 10cm from the axis. The coefficent of friction between the disc and the coin is 0.2. The value of the frictional force on the coin at t=1s will be
View SolutionA uniform disc of mass m and radius R rotates about a fixed vertical axis passing through its centre with angular velocity ω. A particle of same mass m and having velocity of 2ωR towards centre of the disc collides with the disc moving horizontally and sticks to its rim. Then
View Solution
