A body of mass 60 kg is holding a vertical rope . The rope can break when a mass of 75 kg is suspended from it. The maximum acceleration with which the boy can climb the rope without breaking it is :(g=10m/s2)
2.5m/s2
5.0m/s2
7.5m/s2
22.5m/s2
The correct Answer is:1
Step by step video & image solution for A body of mass 60 kg is holding a vertical rope . The rope can break when a mass of 75 kg is suspended from it. The maximum acceleration with which the boy can climb the rope without breaking it is : ( g = 10 m//s^(2)) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE53videos
LAWS OF MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - ENABLE50videos
LAWS OF MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - JEE Advanced (archive)14videos
KINEMATICS OF A PARTICLE
- BOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE ADVANCED (LEVEL -2)55videos
LIQUIDS
Similar Questions
A monkey of mass 20kg is holding a vertical rope. The rope will not break when a mass of 25kg is suspended from it but will break it the mass exeeds 25kg . What is the maximum acceleration with which the monkey can climb up along the rope? (g=10m/s2) .
View SolutionA monkey of mass 20kg is holding a vertical rope. The rope will not break when a mass of 25kg is suspended from it but will break it the mass exeeds 25kg . What is the maximum acceleration with which the monkey can climb up along the rope? (g=10m/s2) .
View SolutionA monkey of 25 kg is holding a vertical rope. The rope does not break if a body of mass less than 30 kg is suspended with the rope. What will be the maximum acceleration with which the monkey can climb up along the rope ? (Take g=10ms−2)
View SolutionThe minimum acceleration with which a fireman can slide down a rope of breaking strength two - third of his weight is
View SolutionA 50 kg man stuck in flood is being lifted vertically by an army helicopter with the help of light rope which can bear a maximum tension of 70 kg-wt. The maximum acceleration with which helicopter can rise so that rope does not breaks is (g=9.8ms−2)
View SolutionBlock B of mass 100 kg rests on a rough surface of friction coeffcient μ=1/3. A rope is tied to block B as shown in figure. The maximum acceleration with which boy A of 24 kg can climbs on rope without making block move is :
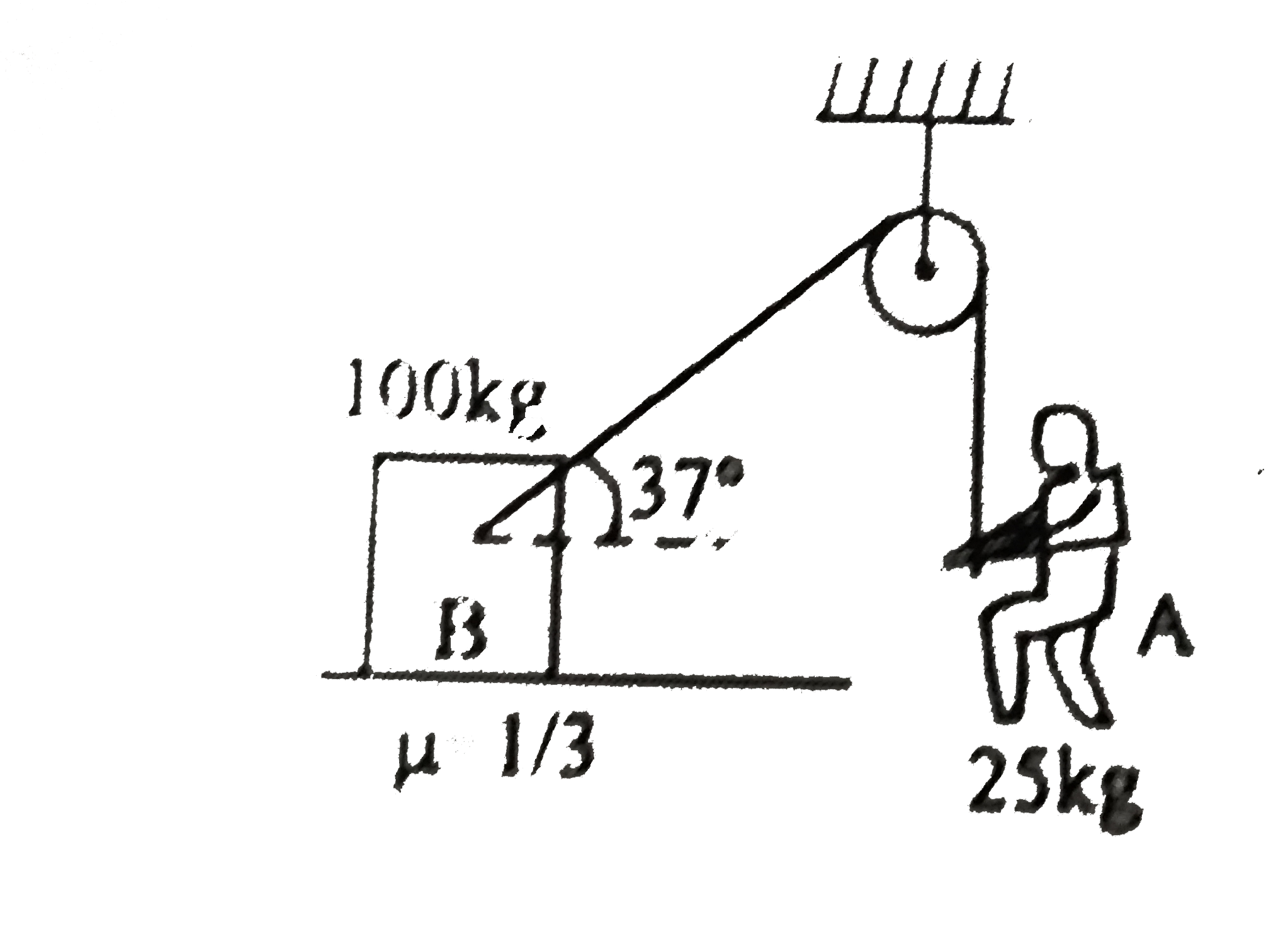 View Solution
View SolutionA boy of mass 40 kg climbs up a rope with an acceleration of 2ms−2 . What is the tension in the rope ?
View SolutionThe maximum tension a rope can withstand is 60 kg.wt. The ratio of maximum acceleration with which two boys of masses 20 kg and 30 kg can climb up the rope at the same time is
View SolutionA particle of mass 100 g tied to a string is rotated along the circle of radius 0.5 m. The breaking tension of the string is 10 N. The maximum speed with which particle can be rotated without breaking the string is
View SolutionA body of mass 50 kg and specific gravity force is to be lifted using a rope of breaking strength of 60 kg wt. The acceleration with which it can be pulled up in least interval of time
View Solution


