Two paricles A and B start simultaneously from the same point and move in a horizontal plane. A has an initial velocity u1 due east and acceleration a1 due north. B has an intial velocity u2 due north and acceleration a2 due east.
Their paths must intersect at some point
They must collide at some point
They will collide only if a1u1=a2u2
If u1>u2 and a1<a2, the particles will have the same speed at some point of time
The correct Answer is:A, C, D
To solve the problem of two particles A and B moving in a horizontal plane with given initial velocities and accelerations, we can break down the solution step by step.
1. Understanding the Motion of Particle A:
- Particle A starts with an initial velocity u1 due east and has an acceleration a1 due north.
- The displacement of particle A after time t can be expressed using the equation of motion:
→SA=u1^it+12a1^jt2
- Here, ^i represents the eastward direction and ^j represents the northward direction.
2. Understanding the Motion of Particle B:
- Particle B starts with an initial velocity u2 due north and has an acceleration a2 due east.
- The displacement of particle B after time t can be expressed as:
→SB=u2^jt+12a2^it2
3. Setting Up the Displacement Equations:
- For particle A:
→SA=u1t^i+12a1t2^j
- For particle B:
→SB=12a2t2^i+u2t^j
4. Finding Conditions for Intersection:
- For the paths of particles A and B to intersect, their displacements must be equal at some time t:
u1t=12a2t2(1)
12a1t2=u2t(2)
5. Dividing the Equations:
- From equations (1) and (2), we can divide them to eliminate t:
u1t12a2t2=12a1t2u2t
- Simplifying gives:
u112a2t=12a1tu2
- This leads to:
u1u2=a2a1
- Rearranging gives:
u1a1=u2a2(3)
6. Analyzing the Options:
- Option 1: Their paths must intersect at some point - Correct (as derived).
- Option 2: They must collide at some point - Incorrect (they will collide only if u1a1=u2a2).
- Option 3: If u1>u2 and a1<a2, they will have the same speed at some point - Correct (from the relationship derived).
Final Conclusion:
The correct options are that their paths must intersect at some point, and if u1>u2 and a1<a2, they will have the same speed at some point.
- Particle A starts with an initial velocity u1 due east and has an acceleration a1 due north.
- The displacement of particle A after time t can be expressed using the equation of motion:
→SA=u1^it+12a1^jt2
- Here, ^i represents the eastward direction and ^j represents the northward direction.
- Particle B starts with an initial velocity u2 due north and has an acceleration a2 due east.
- The displacement of particle B after time t can be expressed as:
→SB=u2^jt+12a2^it2
- For particle A:
→SA=u1t^i+12a1t2^j
- For particle B:
→SB=12a2t2^i+u2t^j
- For the paths of particles A and B to intersect, their displacements must be equal at some time t:
u1t=12a2t2(1)
12a1t2=u2t(2)
- From equations (1) and (2), we can divide them to eliminate t:
u1t12a2t2=12a1t2u2t
- Simplifying gives:
u112a2t=12a1tu2
- This leads to:
u1u2=a2a1
- Rearranging gives:
u1a1=u2a2(3)
- Option 1: Their paths must intersect at some point - Correct (as derived).
- Option 2: They must collide at some point - Incorrect (they will collide only if u1a1=u2a2).
- Option 3: If u1>u2 and a1<a2, they will have the same speed at some point - Correct (from the relationship derived).
The correct options are that their paths must intersect at some point, and if u1>u2 and a1<a2, they will have the same speed at some point.
Topper's Solved these Questions
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:JEE Main (Archive)
Explore 19 Videos
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:JEE Advanced (Archive)
Explore 19 Videos
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:Long Answer Type
Explore 5 Videos
- Motion in Straight Line Book:VMC MODULES ENGLISHChapter:Motion in Straight Line Exercise:IN-CHAPTER EXERCISE-J
Explore 10 Videos
- MOVING CHARGES & MAGNETISM Book:VMC MODULES ENGLISHChapter:MOVING CHARGES & MAGNETISM Exercise:IN-CHAPTER EXERCISE-K
Explore 10 Videos
Similar Questions
A body has an initial velocity of 3ms−1 and has an acceleration of 1ms−2 normal to the direction of the initial velocity. Then its velocity 4s after the start is.
View SolutionA particle has an initial velocity of 9m/s due east and a constant acceleration of 2m/s2 due west. The distance coverd by the particle in the fifth second of its motion is :
View SolutionA body is projected vertically upward with an initial velocity u. If acceleration due to gravity is g, find the time for which it remains in air.
View SolutionCar A has an acceleration of 2m/s2 due east and car B,4m/s2. due north. What is the acceleration of car B with respect to car A?
View SolutionCar A has an acceleration of 2m/s2 due east and car B,4m/s2. due north. What is the acceleration of car B with respect to car A?
View SolutionTwo cars A and B start moving from the same point with same velocity v=5km/minute. Car A moves towards North and car B in moving towards East. What is the relative velocity of B with respect to A ?
View SolutionA man walks for some time 't' with velocity(v) due east. Then he walks for same time 't' with velocity (v) due north. The average velocity of the man is:-
View SolutionTwo particles are thrown simultaneously from points A and B with velocities u1=2ms−1andu2−14ms−1, respectively, as shown in figure.
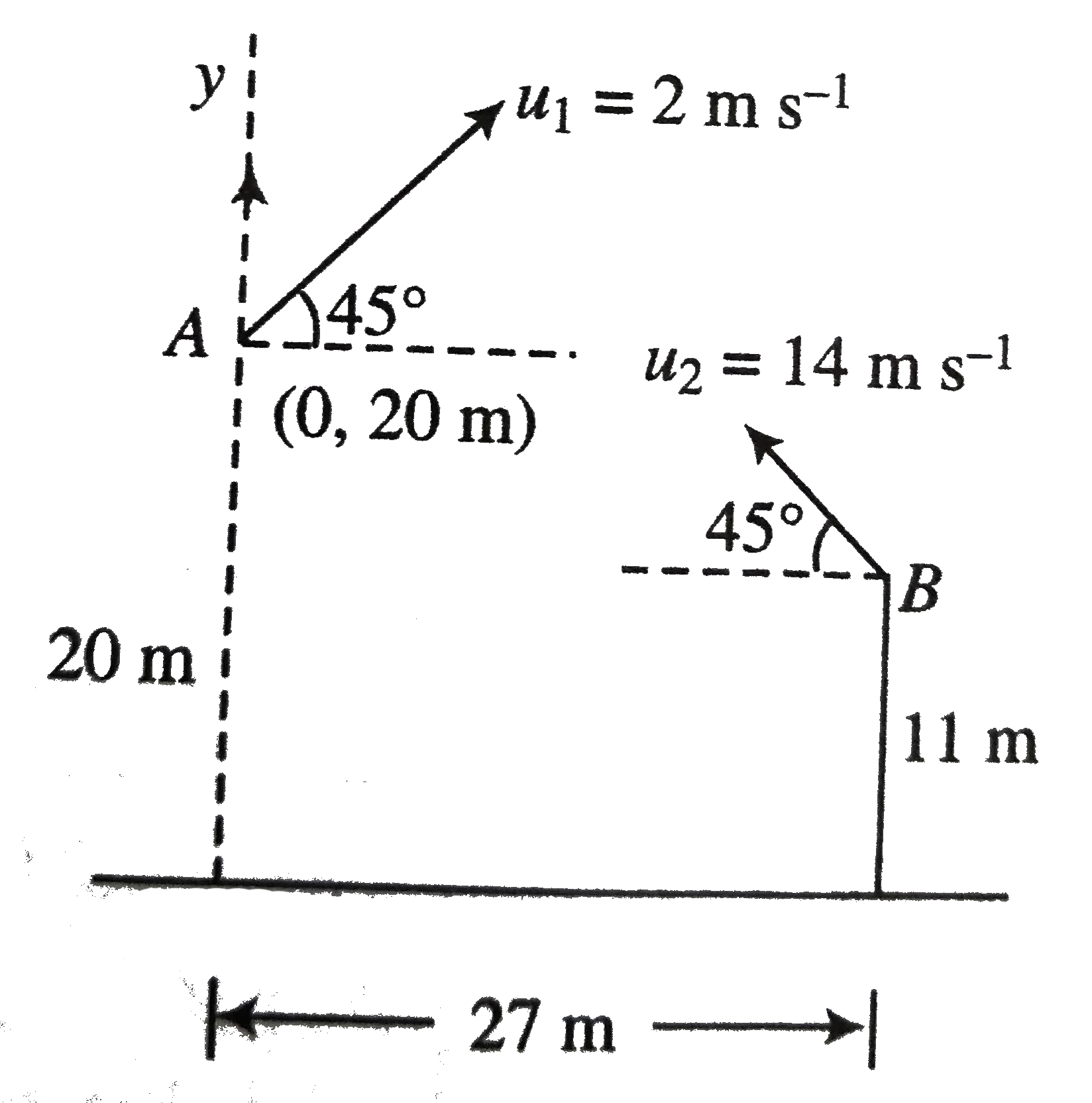
The relative velocity of B as seen from A in
View SolutionA sphere and a disc of same radii and mass are rolling on an inclined plane without slipping. as & ad are acceleration and g is acceleration due to gravity. Then which statement is correct?
View SolutionTwo particles are thrown simultaneously from points A and B with velocities u1=2ms−1andu2−14ms−1, respectively, as shown in figure.
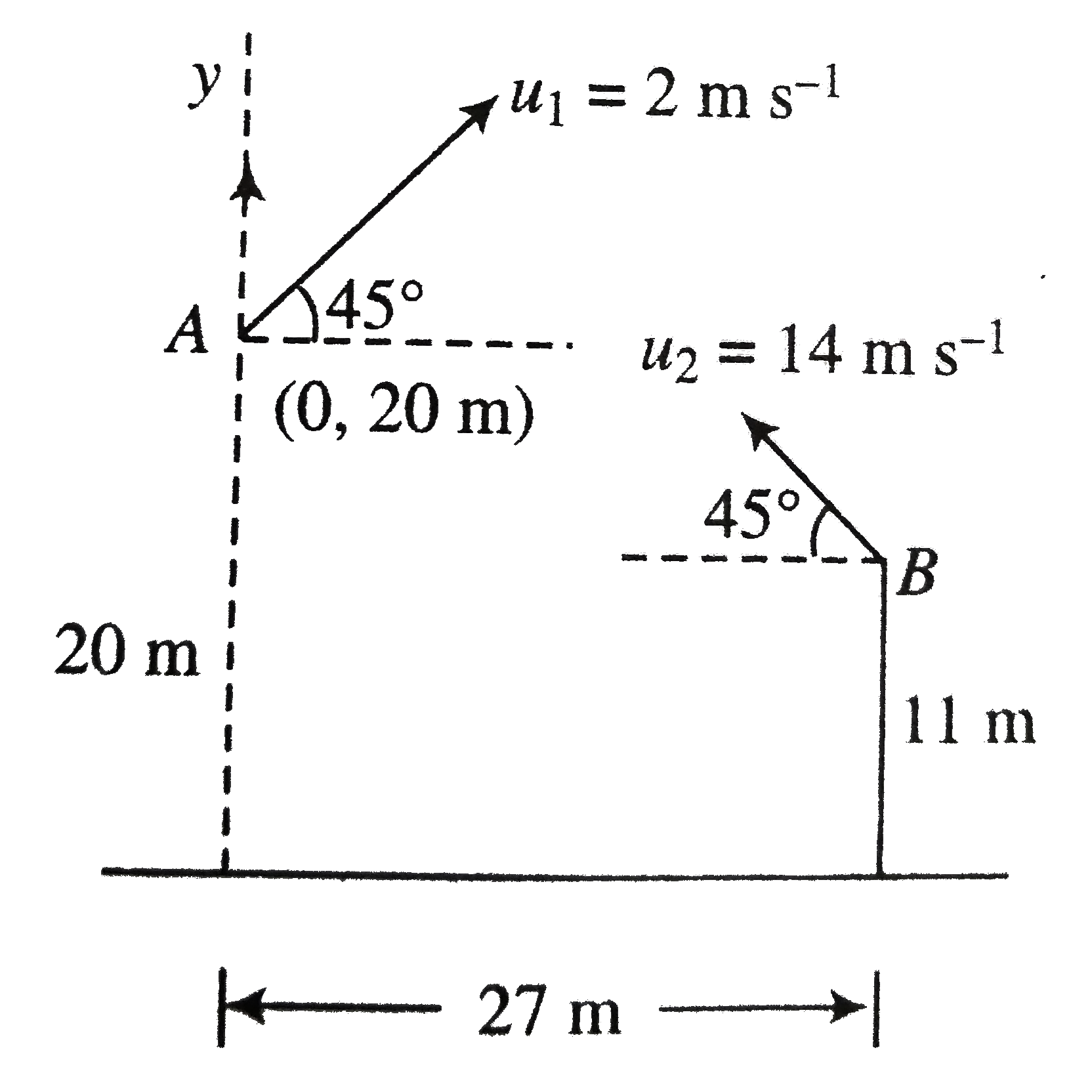
Minimum separation between A and B is
View Solution

