A projectile of mass has velocities and at two points during its flight in the uniform gravitational field of the earth. If these two velocities are perpendicular to each other, then the minimum kinetic enerty of the particle during its flight is
6.32 J
8.40 J
16.32 J
5.76 J
The correct Answer is:D
To solve the problem, we need to find the minimum kinetic energy of a projectile given that it has two velocities that are perpendicular to each other. Let's break down the solution step by step.
Step 1: Understand the Given Information
We have a projectile of mass m=2kg with two velocities:
- v1=3m/s
- v2=4m/s
These velocities are perpendicular to each other.
Step 2: Use the Relationship Between Velocities
Since the velocities are perpendicular, we can use the relationship of their components. Let's denote the angle of v1 with the horizontal as α. The angle of v2 will then be 90∘−α.
The horizontal components of the velocities must be equal because there is no horizontal acceleration in projectile motion:
v1cos(α)=v2cos(90∘−α)=v2sin(α)
Substituting the values:
3cos(α)=4sin(α)
Step 3: Solve for tan(α)
Rearranging the equation gives:
cos(α)sin(α)=43
Thus,
tan(α)=34
Step 4: Find cos(α) and sin(α)
Using the identity tan(α)=oppositeadjacent:
- Let the opposite side be 3 and the adjacent side be 4.
- The hypotenuse h can be calculated using Pythagoras' theorem:
h=√32+42=√9+16=5
Thus,
sin(α)=35,cos(α)=45
Step 5: Calculate ucos(θ)
The minimum velocity occurs at the highest point of the projectile's motion, which is given by:
ucos(θ)=v1cos(α)=3⋅45=125m/s
Step 6: Calculate Minimum Kinetic Energy
The kinetic energy KE is given by:
KE=12m(ucos(θ))2
Substituting the values:
KE=12⋅2⋅(125)2
KE=1⋅14425=14425J
Step 7: Convert to Decimal Form
To express this in decimal form:
14425=5.76J
Final Answer
Thus, the minimum kinetic energy of the projectile during its flight is:
5.76J
We have a projectile of mass m=2kg with two velocities:
- v1=3m/s
- v2=4m/s
Since the velocities are perpendicular, we can use the relationship of their components. Let's denote the angle of v1 with the horizontal as α. The angle of v2 will then be 90∘−α.
v1cos(α)=v2cos(90∘−α)=v2sin(α)
Substituting the values:
3cos(α)=4sin(α)
Rearranging the equation gives:
cos(α)sin(α)=43
Thus,
tan(α)=34
Using the identity tan(α)=oppositeadjacent:
- Let the opposite side be 3 and the adjacent side be 4.
- The hypotenuse h can be calculated using Pythagoras' theorem:
h=√32+42=√9+16=5
Thus,
sin(α)=35,cos(α)=45
The minimum velocity occurs at the highest point of the projectile's motion, which is given by:
ucos(θ)=v1cos(α)=3⋅45=125m/s
The kinetic energy KE is given by:
KE=12m(ucos(θ))2
Substituting the values:
KE=12⋅2⋅(125)2
KE=1⋅14425=14425J
To express this in decimal form:
14425=5.76J
Thus, the minimum kinetic energy of the projectile during its flight is:
5.76J
Topper's Solved these Questions
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:JEE Main (Archive)
Explore 19 Videos
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:JEE Advanced (Archive)
Explore 19 Videos
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:Long Answer Type
Explore 5 Videos
- Motion in Straight Line Book:VMC MODULES ENGLISHChapter:Motion in Straight Line Exercise:IN-CHAPTER EXERCISE-J
Explore 10 Videos
- MOVING CHARGES & MAGNETISM Book:VMC MODULES ENGLISHChapter:MOVING CHARGES & MAGNETISM Exercise:IN-CHAPTER EXERCISE-K
Explore 10 Videos
Similar Questions
Two bodies of different masses 2kg and 4kg are moving with velocities 2m/s and 10m/s towards each other due to mutual gravitational attraction. Then the velocity of the centre of mass is
View SolutionTwo smooth spheres A and B of masses 4kg and 8kg move with velocities 9m/s and 3m/s in opposite directions. If A rebounds on its path with velocity 1m/s, then
View SolutionA particle of mass 1 kg has a velocity of 2m/s. A constant force of 2N acts on the particle for 1s in a direction perpendicular to its initial velocity. Find the velocity and displacement of the particle at the end of 1 s.
View SolutionTwo rings of radii 5m and 10m move in opposite directions with velocity 20 m/s and 10 m/s respectively, on a conducting curface S. There is a uniform magnetic field of magnitude 0.1T perpendicular to the plane of the rings. Find the potential difference between the highest points of the two rings.
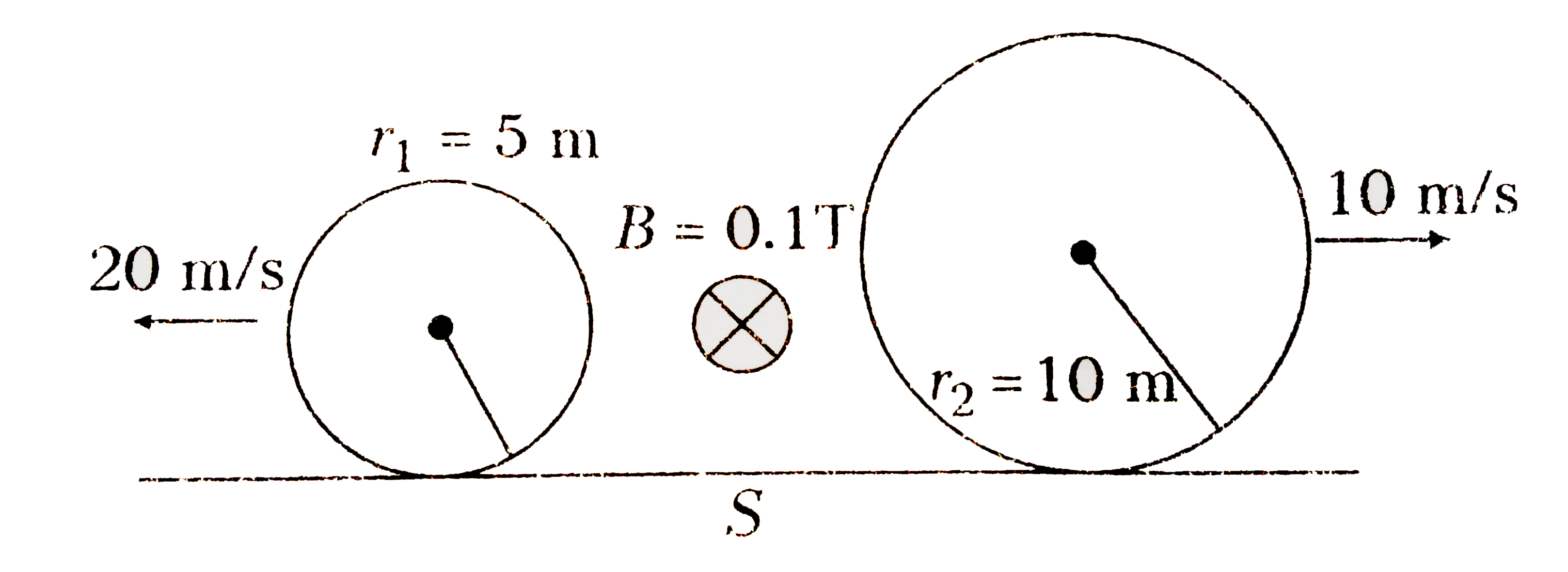
View SolutionTwo particles are performing SHM with same amplitude and time period. At an instant two particles are having velocity 1m/s but one is on the right and the other is on left of their mean positiion. When the particles have same position there speed is √3m/s. Find the maximum speed (in m/s) of particles during SHM.
View SolutionA particle of mass m is projected at an angle α to the horizontal with an initial velocity u. The work done by gravity during the time it reaches its highest point is
View SolutionA car is travelling at a velocity of 10 m/s and has a mass of 850 kg. What is its kinetic energy?
View SolutionWhen a particle is projected at some angle with the horizontal, the path of the particle is parabolic. In the process the horizontal velocity remains constant but the magnitude of vertical velocity changes. At any instant during flight the acceleration of the particle remains g in vertically downward direction. During flight at any point the path of particle can be considered as a part of circle and radius of that circle is called the radius of curvature of the path
Consider that a particle is projected with velocity u=10m/s at an angle θ=60∘ with the horizontal and take value of g=10m/s2. Now answer the following questions.
The radius of curvature of path of particle at the instant when the velocity vector of the particle becomes perpendicular to initial velocity vector is
View SolutionA particle of mass m and charge Q moving with a velocity v enters a region on uniform field of induction B Then its path in the region is s
View SolutionA projectile is thrown at an angle of 30∘ with a velocity of 10m/s. the change in velocity during the time interval in which it reaches the highest point is
View Solution

