Time of flight is 1 s and range is 4 m .Find the projection speed is:
√37ms−1
√41ms−1
√14ms−1
√40ms−1
The correct Answer is:B
To find the projection speed given the time of flight and range, we can follow these steps:
Step 1: Understand the given information
- Time of flight (T) = 1 s
- Range (R) = 4 m
- Acceleration due to gravity (g) = 10 m/s² (approximately)
Step 2: Use the formula for time of flight
The formula for time of flight in projectile motion is given by:
T=2usinθg
Substituting the known values:
1=2usinθ10
Rearranging gives:
usinθ=g2=102=5 m/s
Step 3: Use the formula for range
The formula for range in projectile motion is given by:
R=u2sin2θg
Substituting the known values:
4=u2sin2θ10
Rearranging gives:
u2sin2θ=40
Step 4: Relate sin 2θ to sin θ and cos θ
Using the identity sin2θ=2sinθcosθ, we can rewrite the range equation:
u2(2sinθcosθ)=40
This simplifies to:
u2sinθcosθ=20
Step 5: Solve for u
We have two equations now:
1. usinθ=5
2. u2sinθcosθ=20
From the first equation, we can express sinθ in terms of u:
sinθ=5u
Substituting this into the second equation:
u2(5u)cosθ=20
This simplifies to:
5ucosθ=20
Thus, we have:
ucosθ=4 m/s
Step 6: Find the projection speed
Now we have:
- usinθ=5
- ucosθ=4
Using the Pythagorean theorem:
u=√(usinθ)2+(ucosθ)2
Substituting the values:
u=√52+42=√25+16=√41
Final Answer
The projection speed u is:
u=√41 m/s
---
- Time of flight (T) = 1 s
- Range (R) = 4 m
- Acceleration due to gravity (g) = 10 m/s² (approximately)
The formula for time of flight in projectile motion is given by:
T=2usinθg
Substituting the known values:
1=2usinθ10
Rearranging gives:
usinθ=g2=102=5 m/s
The formula for range in projectile motion is given by:
R=u2sin2θg
Substituting the known values:
4=u2sin2θ10
Rearranging gives:
u2sin2θ=40
Using the identity sin2θ=2sinθcosθ, we can rewrite the range equation:
u2(2sinθcosθ)=40
This simplifies to:
u2sinθcosθ=20
We have two equations now:
1. usinθ=5
2. u2sinθcosθ=20
sinθ=5u
u2(5u)cosθ=20
This simplifies to:
5ucosθ=20
Thus, we have:
ucosθ=4 m/s
Now we have:
- usinθ=5
- ucosθ=4
u=√(usinθ)2+(ucosθ)2
Substituting the values:
u=√52+42=√25+16=√41
The projection speed u is:
u=√41 m/s
Topper's Solved these Questions
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:JEE Main (Archive)
Explore 19 Videos
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:JEE Advanced (Archive)
Explore 19 Videos
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:Long Answer Type
Explore 5 Videos
- Motion in Straight Line Book:VMC MODULES ENGLISHChapter:Motion in Straight Line Exercise:IN-CHAPTER EXERCISE-J
Explore 10 Videos
- MOVING CHARGES & MAGNETISM Book:VMC MODULES ENGLISHChapter:MOVING CHARGES & MAGNETISM Exercise:IN-CHAPTER EXERCISE-K
Explore 10 Videos
Similar Questions
An arrow is shot in air, its time of flight is 5 sec and horizontal range is 200 m. the inclination of the arrow with the horizontal is
View SolutionFind time of flight and range of the projectile along the inclined plane as shown in figure. (g=10m/s2)
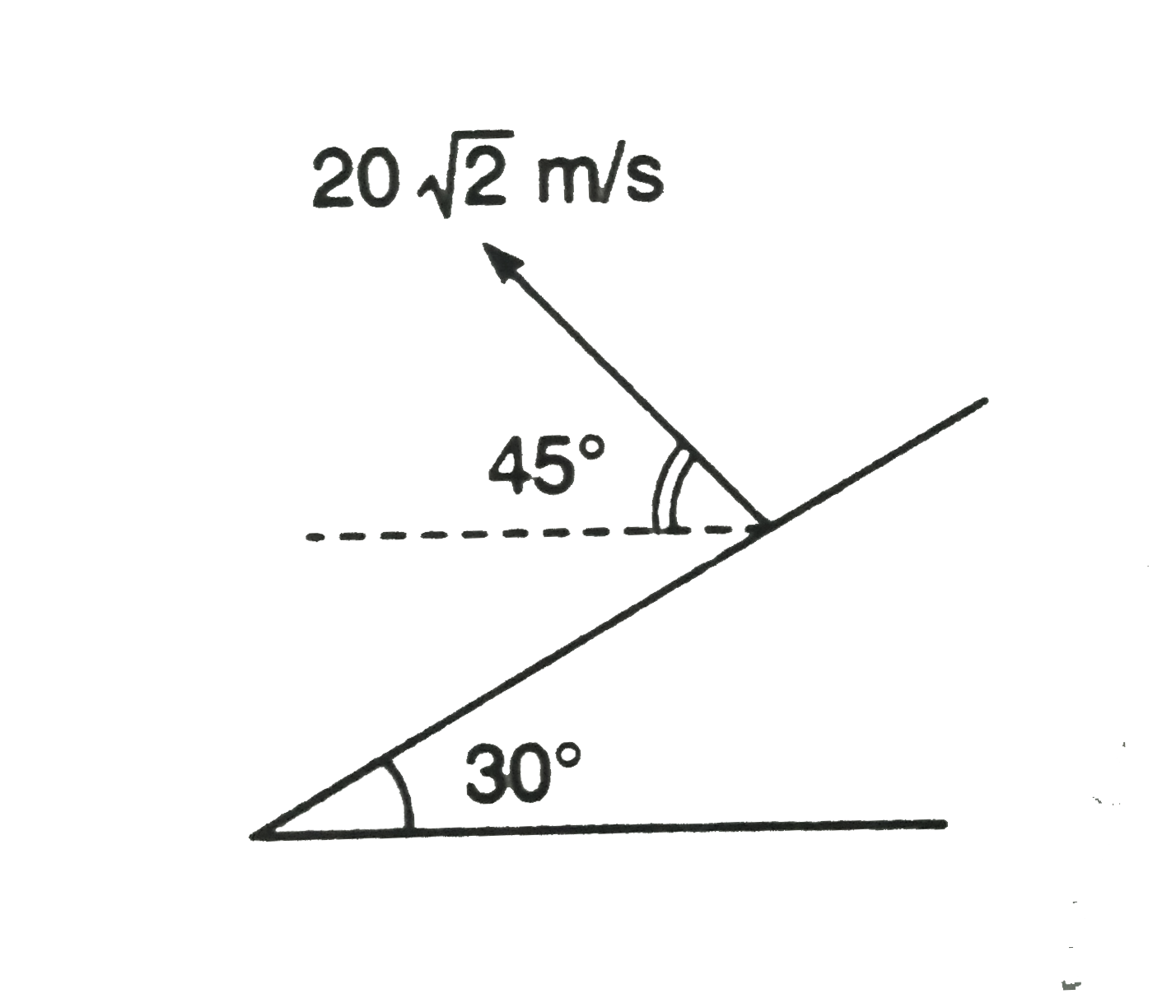
View SolutionFind time of flight and range of the projectile along the inclined plane as shown in figure. (g=10m/s2)

View SolutionFind time of flight and range of the projectile along the inclined plane as shown in figure. (g=10m/s2)
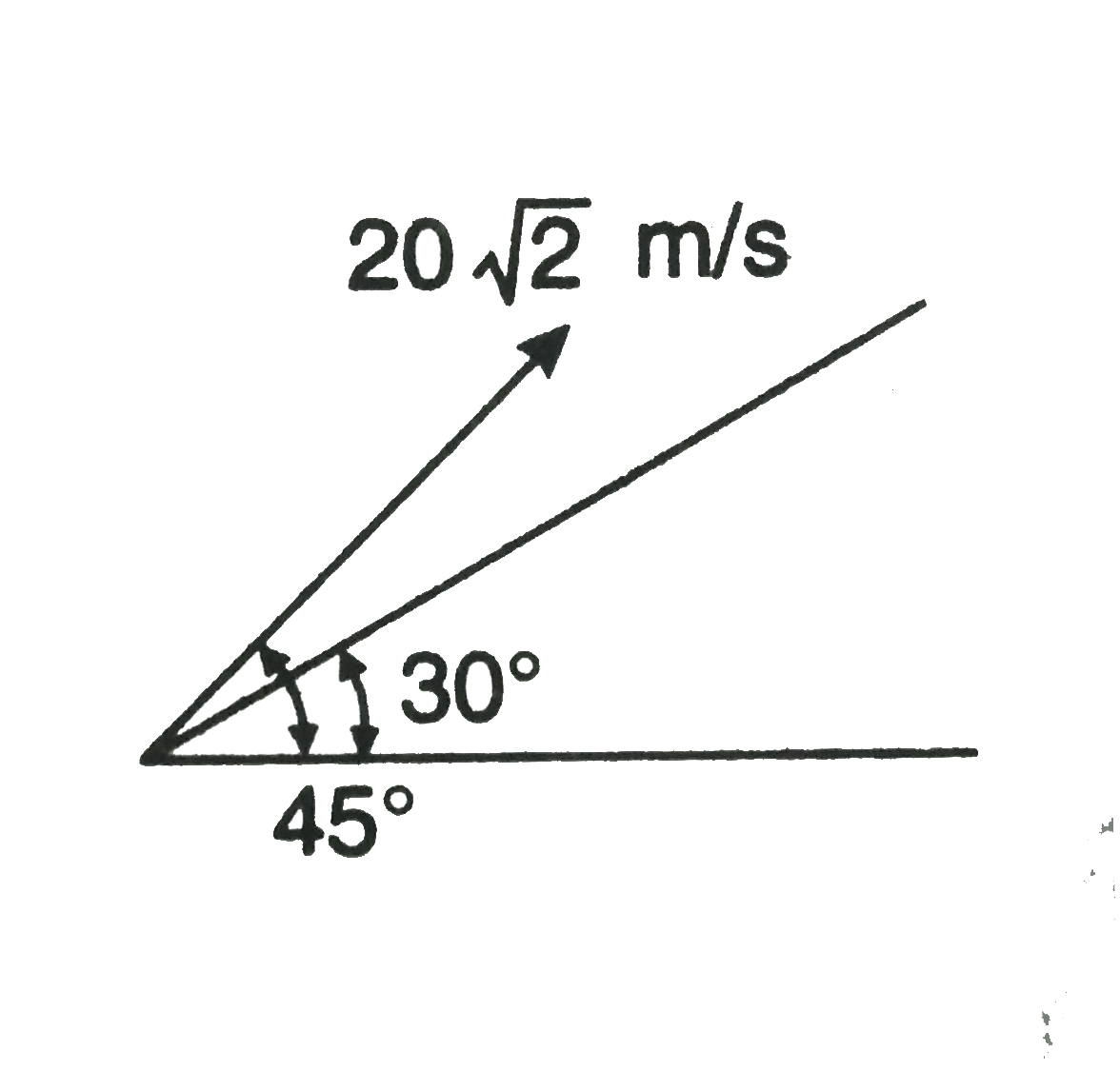
View SolutionA stone is projected in air. Its time of flight is 3s and range is 150m. Maximum height reached by the stone is (Take, g=10ms−2)
View SolutionAn arrow is projected into air. It's time of flight is 5seconds and range 200m. , the vertical component of the velocity is:-
View SolutionA particle is projected up the inclined such that its component of velocity along the incline is 10m/s. Time of flight is 2 sec and maximum height above the incline is 5m. Then velocity of projection will be
View SolutionA projectile has a range R and time of flight T. If the range is doubled (by increasing the speed of projection, without changing the angle of projection), the time of flight will become
View SolutionWhen a particle is projected at an angle to the horizontal, it has range R and time of flight t1. If the same projectile is projected with same speed at another angle to have the saem range, time of flight is t2. Show that:
t1t2=(2R/g)
View SolutionA projectile has a time of flight T and range R. If the time of flight is doubled, keeping the angle of projection same, what happens to the range ?
View Solution

