Find the ratio of horizontal range and the height attained by the projectile. i.e. for θ=45∘
1
4
1/4
1/2
The correct Answer is:D
To find the ratio of the horizontal range to the maximum height attained by a projectile when the launch angle θ=45∘, we can follow these steps:
Step 1: Write the formulas for horizontal range and maximum height.
The formulas for the horizontal range R and maximum height H of a projectile are given by:
- Horizontal Range:
R=u2sin2θg
- Maximum Height:
H=u2sin2θ2g
Step 2: Set up the ratio of horizontal range to maximum height.
We need to find the ratio RH:
RH=u2sin2θgu2sin2θ2g
Step 3: Simplify the ratio.
Cancel out u2 and g from the numerator and denominator:
RH=sin2θ12sin2θ=2sin2θsin2θ
Step 4: Substitute θ=45∘.
Now, substitute θ=45∘ into the equation:
- We know that sin2θ=sin90∘=1.
- Also, sin45∘=1√2.
Thus, we have:
RH=2⋅1(1√2)2=212=2⋅2=4
Step 5: Conclusion.
The ratio of the horizontal range to the maximum height attained by the projectile when θ=45∘ is:
RH=4
The formulas for the horizontal range R and maximum height H of a projectile are given by:
- Horizontal Range:
R=u2sin2θg
- Maximum Height:
H=u2sin2θ2g
We need to find the ratio RH:
RH=u2sin2θgu2sin2θ2g
Cancel out u2 and g from the numerator and denominator:
RH=sin2θ12sin2θ=2sin2θsin2θ
Now, substitute θ=45∘ into the equation:
- We know that sin2θ=sin90∘=1.
- Also, sin45∘=1√2.
RH=2⋅1(1√2)2=212=2⋅2=4
The ratio of the horizontal range to the maximum height attained by the projectile when θ=45∘ is:
RH=4
Topper's Solved these Questions
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:JEE Main (Archive)
Explore 19 Videos
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:JEE Advanced (Archive)
Explore 19 Videos
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:Long Answer Type
Explore 5 Videos
- Motion in Straight Line Book:VMC MODULES ENGLISHChapter:Motion in Straight Line Exercise:IN-CHAPTER EXERCISE-J
Explore 10 Videos
- MOVING CHARGES & MAGNETISM Book:VMC MODULES ENGLISHChapter:MOVING CHARGES & MAGNETISM Exercise:IN-CHAPTER EXERCISE-K
Explore 10 Videos
Similar Questions
Find the ratio of maximum horizontal range and the maximum height attained by the projectile. i.e. for θ0=45∘
View SolutionProve that the maximum horizontal range is four times the maximum height attained by the projectile, when fired at an inclination so as to have maximum horizontal range.
View Solution
Knowledge Check
Galileo writes that for angles of projection of a projectile at angles (45+θ) and (45−θ), the horizontal ranges described by the projectile are in the ratio of (if θ≤45)
A2:1B1:2C1:1D2:3
Prove that the maximum horizontal range is four times the maximum height attained by the projectile, when fired at an inclination so as to have maximum horizontal range.
View SolutionIf R and H are the horizontal range and maximum height attained by a projectile , than its speed of prjection is
View SolutionA projectile is projected from the ground by making an angle of 60∘ with the horizontal. After 1 s projectile makes an angle of 30∘ with the horizontal . The maximum height attained by the projectile is (Take g=10ms−2)
View SolutionAssertion: In projectile motion, when horizontal range is n times the maximum height, the angle of projection is given by tanθ=4n
Reason: In the case of horizontal projection the vertical increases with time.
View SolutionIf R is the horizontal range for θ inclination and h is the maximum height reached by the projectile, show that the maximum ragne is given by R28h+2h.
View SolutionA projectile is projected with a speed = 20 m/s from the floor of a 5 m high room as shown. Find the maximum horizontal range of the projectile and the corresponding angle of projection θ.
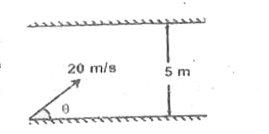
View SolutionFor angles of projection of a projectile at angle (45∘−θ)and(45∘+θ), the horizontal ranges described by the projectile are in the ratio of :
View Solution