A block of mass 4kg rests on a rough horizontal plane. The plane is gradually inclined until at an angle θ=60∘ , with the vertical, the mass just begins to side. What is the coefficient of static friction between the block and the plane?
√3
12
1√2
1√3
The correct Answer is:D
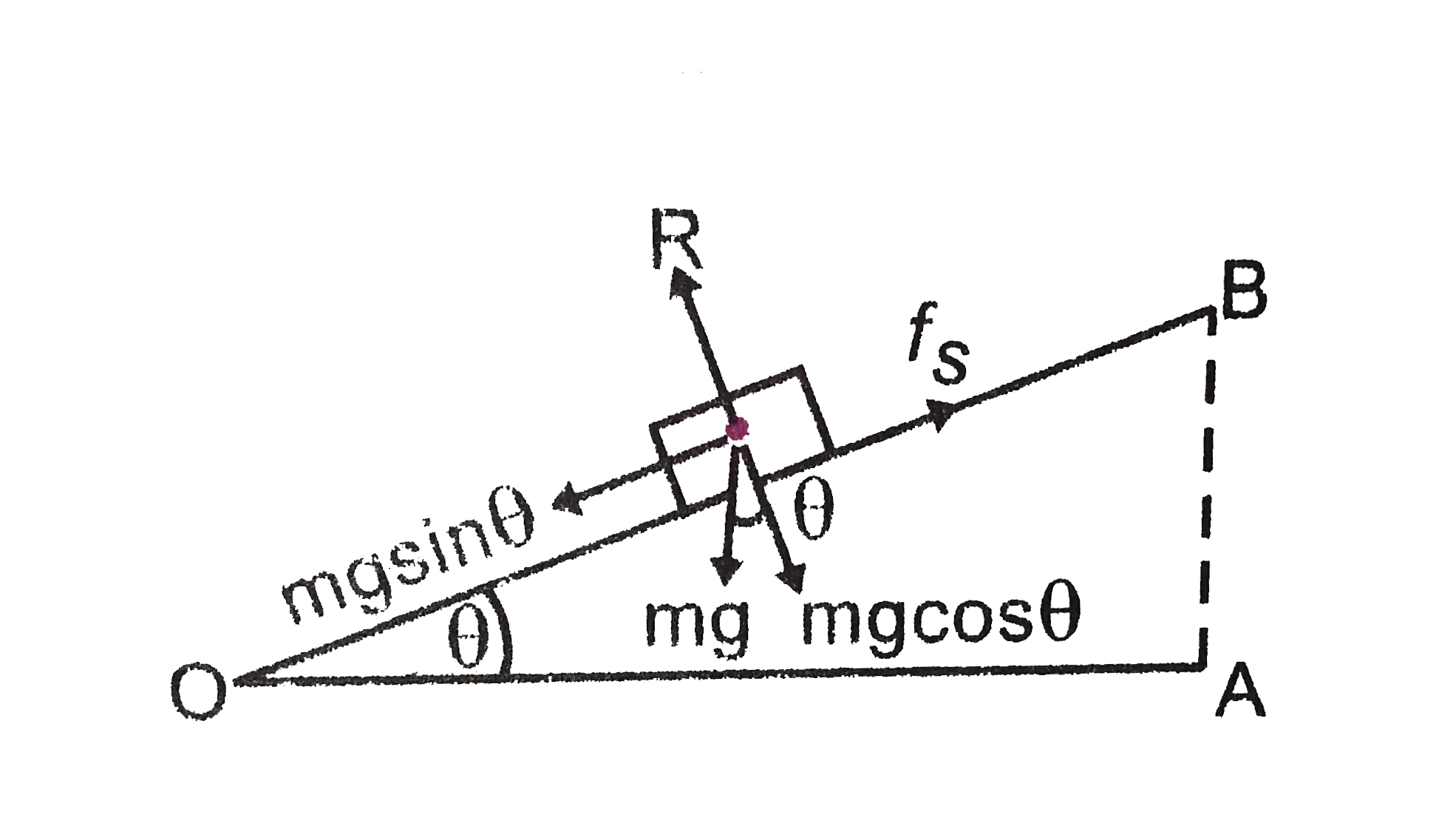
To solve the problem of finding the coefficient of static friction between a block of mass 4 kg resting on a rough horizontal plane that begins to slide when the plane is inclined at an angle of θ = 60° with the vertical, we can follow these steps:
Step 1: Understanding the Angle
The angle θ is given as 60° with the vertical. To find the angle with the horizontal, we can use the relationship:
Angle with horizontal=90°−θ=90°−60°=30°
Step 2: Drawing the Free Body Diagram (FBD)
We draw the block on the inclined plane. The forces acting on the block are:
- The gravitational force (weight) W=mg acting downwards.
- The normal force N acting perpendicular to the surface of the incline.
- The frictional force Ff acting parallel to the incline, opposing the motion.
Step 3: Resolving the Weight into Components
The weight of the block can be resolved into two components:
- Perpendicular to the incline: W⊥=mgcos(30°)
- Parallel to the incline: W∥=mgsin(30°)
Given m=4kg and g=10m/s2:
W=mg=4×10=40N
Now, we calculate the components:
W⊥=40cos(30°)=40×√32=20√3N
W∥=40sin(30°)=40×12=20N
Step 4: Normal Force
The normal force N is equal to the perpendicular component of the weight:
N=W⊥=20√3N
Step 5: Frictional Force
The frictional force Ff must equal the parallel component of the weight when the block is about to slide:
Ff=W∥=20N
Step 6: Coefficient of Static Friction
The frictional force can also be expressed in terms of the coefficient of static friction μ and the normal force:
Ff=μN
Substituting the known values:
20=μ(20√3)
Solving for μ:
μ=2020√3=1√3
Final Answer
The coefficient of static friction μ is:
μ=1√3≈0.577
The angle θ is given as 60° with the vertical. To find the angle with the horizontal, we can use the relationship:
Angle with horizontal=90°−θ=90°−60°=30°
We draw the block on the inclined plane. The forces acting on the block are:
- The gravitational force (weight) W=mg acting downwards.
- The normal force N acting perpendicular to the surface of the incline.
- The frictional force Ff acting parallel to the incline, opposing the motion.
The weight of the block can be resolved into two components:
- Perpendicular to the incline: W⊥=mgcos(30°)
- Parallel to the incline: W∥=mgsin(30°)
W=mg=4×10=40N
Now, we calculate the components:
W⊥=40cos(30°)=40×√32=20√3N
W∥=40sin(30°)=40×12=20N
The normal force N is equal to the perpendicular component of the weight:
N=W⊥=20√3N
The frictional force Ff must equal the parallel component of the weight when the block is about to slide:
Ff=W∥=20N
The frictional force can also be expressed in terms of the coefficient of static friction μ and the normal force:
Ff=μN
Substituting the known values:
20=μ(20√3)
Solving for μ:
μ=2020√3=1√3
The coefficient of static friction μ is:
μ=1√3≈0.577
Topper's Solved these Questions
- INTRODUCTION TO VECTORS & FORCES Book:VMC MODULES ENGLISHChapter:INTRODUCTION TO VECTORS & FORCES Exercise:level 2
Explore 65 Videos
- INTRODUCTION TO VECTORS & FORCES Book:VMC MODULES ENGLISHChapter:INTRODUCTION TO VECTORS & FORCES Exercise:JEE Main ( ARCHIVE ) ( LEVEL-1)
Explore 12 Videos
- INTRODUCTION TO VECTORS & FORCES Book:VMC MODULES ENGLISHChapter:INTRODUCTION TO VECTORS & FORCES Exercise:JEE Advanced ( ARCHIVE LEVEL-2)
Explore 12 Videos
- GRAVITATIONBook:VMC MODULES ENGLISHChapter:GRAVITATIONExercise:JEE Advance (Archive) TRUE/FALSE
Explore 1 Video
- JEE MAIN - 5Book:VMC MODULES ENGLISHChapter:JEE MAIN - 5Exercise:PART I : PHYSICS (SECTION - 2)
Explore 5 Videos
Similar Questions
A mass of 2kg rests on a horizontal plane. The plane is gradually inclined until at an angle θ=20∘ with the horizontal, the mass just begins to slides. What is the coefficient of static friction between the block and the surface ?
View SolutionA mass of 4 kg rest on a horizontal plane . The plane is gradually inclined until an angle 0=15∘ with the horizontal and the mass just begins to slide . What is the coefficient of static friction between the block and the surface ?
View SolutionA block of mass 5 kg rests on a inclined plane at an angle of 30∘ with the horizontal. If the block just begins to slide, then what is the coefficient of static friction between the block and the surface?
View SolutionA block of mass 5 kg rests on a inclined plane at an angle of 30∘ with the horizontal. If the block just begins to slide, then what is the coefficient of static friction between the block and the surface?
View SolutionA block of mass 5 kg rests on a inclined plane at an angle of 30∘ with the horizontal. If the block just begins to slide, then what is the coefficient of static friction between the block and the surface?
View SolutionA block of mass m lying on a rough horizontal plane is acted upon by a horizontal force P and another force Q inclined at an angle θ to the vertical. The minimum value of coefficient of friction of friction between the block and the surface for which the block will remain in equilibrium is

View SolutionA block of mass m lying on a rough horizontal plane is acted upon by a horizontal force P and another force Q inclined at an angle θ to the vertical. The minimum value of coefficient of friction of friction between the block and the surface for which the block will remain in equilibrium is

View SolutionA block of mass m lying on a rough horizontal plane is acted upon by a horizontal force P and another force Q inclined at an angle θ to the vertical. The minimum value of coefficient of friction of friction between the block and the surface for which the block will remain in equilibrium is

View SolutionA block of mass 5 kg is placed on a rough inclined plane. The inclination of the plane is gradually increased till the block just begins to slide down. The inclination of the plane is than 3 in 5. The coefficient of friction between the block and the plane is (Take, g=10m/s2)
View SolutionA block of mass m lying on a rough horizontal plance is acted upon by a horizontal force P and another force Q inclined at an angle θ to the vertical. The block will remain in equilibrium, if the coefficient of friction between it and the surface is
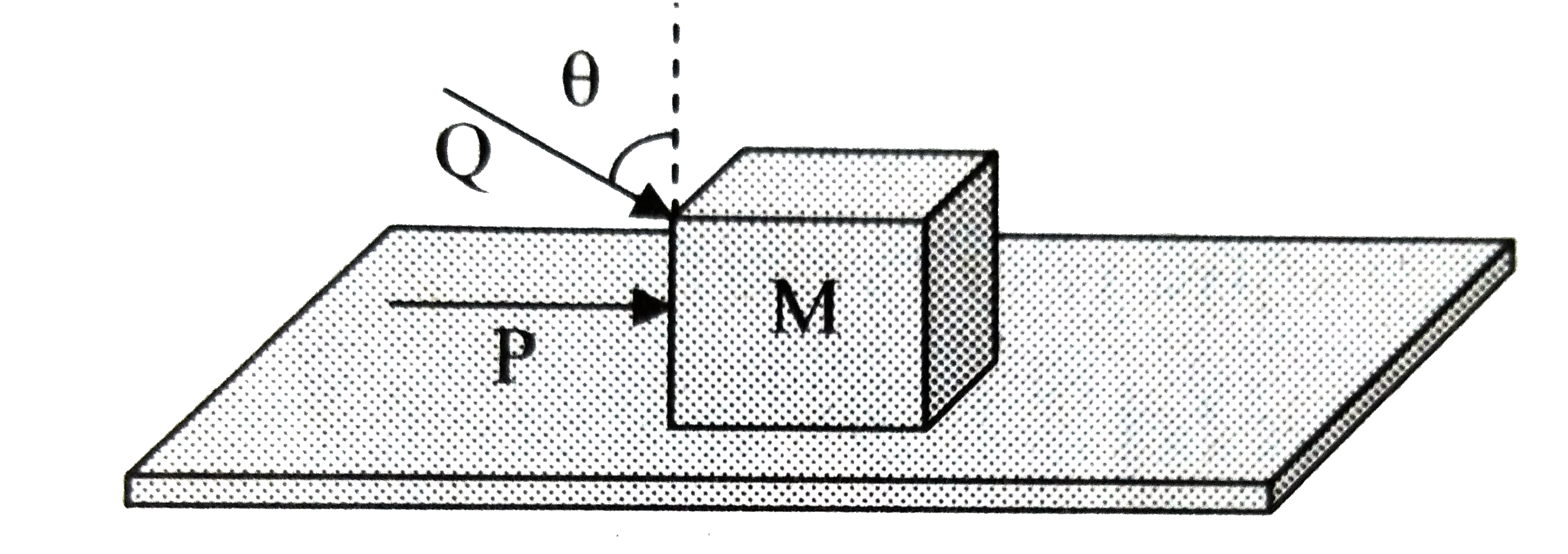
View Solution