A block of mass 5 kg rests on a inclined plane at an angle of 30∘ with the horizontal. If the block just begins to slide, then what is the coefficient of static friction between the block and the surface?
To find the coefficient of static friction between the block and the inclined plane, we can follow these steps:
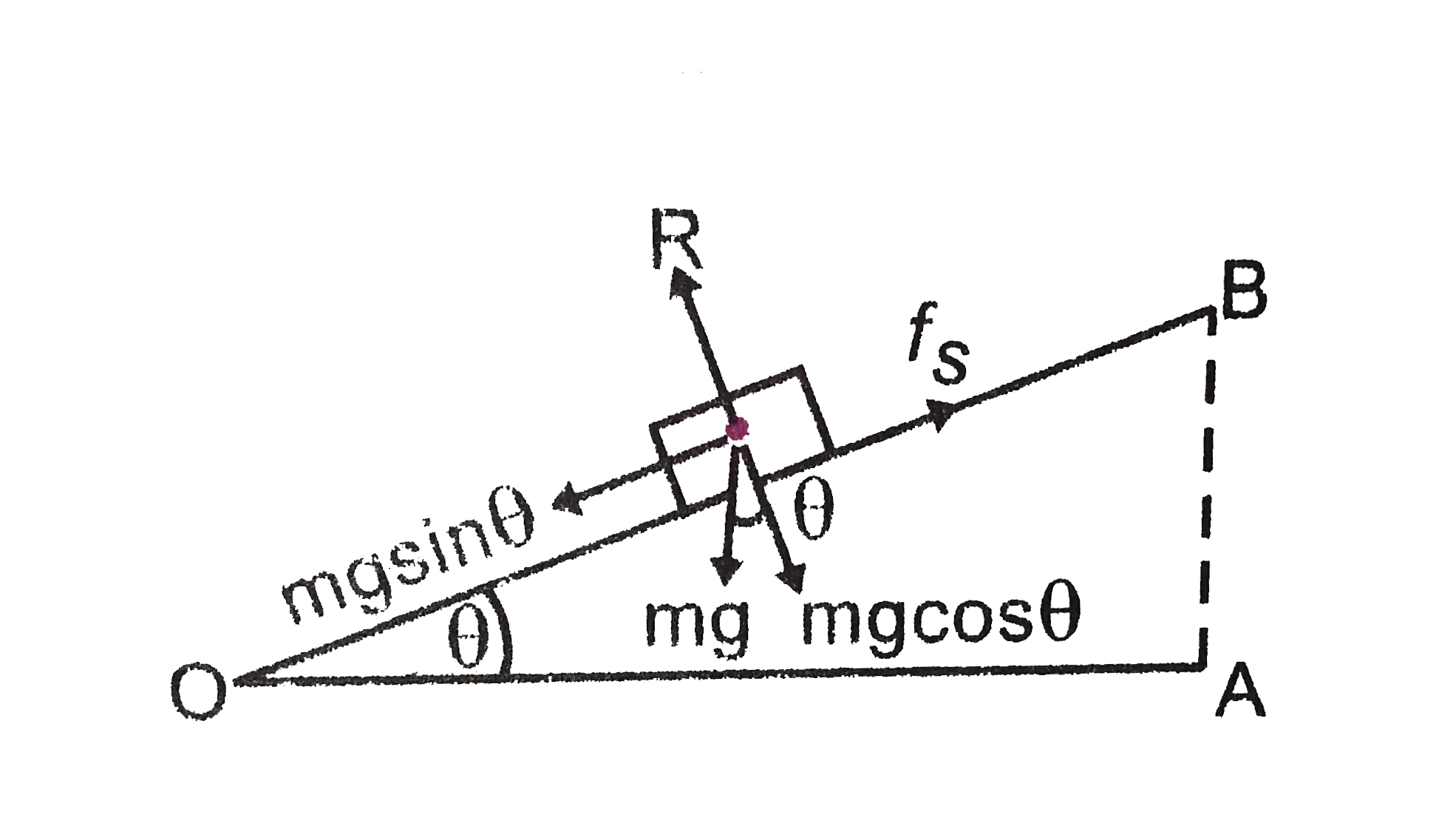
Step 1: Identify the forces acting on the block
When the block is on the inclined plane, the forces acting on it include:
- The gravitational force (weight) acting downwards, which can be resolved into two components:
- Parallel to the incline: mgsinθ
- Perpendicular to the incline: mgcosθ
Step 2: Set up the equations for static equilibrium
Since the block is just about to slide, the static friction force (fs) is at its maximum value and balances the component of gravitational force acting down the incline:
fs=mgsinθ
The normal force (N) acting on the block is equal to the perpendicular component of the weight:
N=mgcosθ
Step 3: Relate static friction to the normal force
The maximum static friction can also be expressed in terms of the coefficient of static friction (μs) and the normal force:
fs=μsN
Step 4: Substitute the expressions for friction and normal force
From the equations above, we can substitute for fs and N:
mgsinθ=μs(mgcosθ)
Step 5: Simplify the equation
We can cancel mg from both sides (assuming m≠0):
sinθ=μscosθ
Step 6: Solve for the coefficient of static friction
Rearranging gives:
μs=sinθcosθ=tanθ
Step 7: Calculate the coefficient of static friction for θ=30∘
Using the known value:
tan30∘=1√3≈0.577
Conclusion
Thus, the coefficient of static friction (μs) between the block and the surface is approximately:
μs≈0.577
When the block is on the inclined plane, the forces acting on it include:
- The gravitational force (weight) acting downwards, which can be resolved into two components:
- Parallel to the incline: mgsinθ
- Perpendicular to the incline: mgcosθ
Since the block is just about to slide, the static friction force (fs) is at its maximum value and balances the component of gravitational force acting down the incline:
fs=mgsinθ
N=mgcosθ
The maximum static friction can also be expressed in terms of the coefficient of static friction (μs) and the normal force:
fs=μsN
From the equations above, we can substitute for fs and N:
mgsinθ=μs(mgcosθ)
We can cancel mg from both sides (assuming m≠0):
sinθ=μscosθ
Rearranging gives:
μs=sinθcosθ=tanθ
Using the known value:
tan30∘=1√3≈0.577
Thus, the coefficient of static friction (μs) between the block and the surface is approximately:
μs≈0.577
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE
69 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-A)
65 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - ASSIGNMENT ( SECTION -J ) Aakash Challengers Questions
12 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
Similar Questions
A mass of 2kg rests on a horizontal plane. The plane is gradually inclined until at an angle θ=20∘ with the horizontal, the mass just begins to slides. What is the coefficient of static friction between the block and the surface ?
View SolutionA mass of 4 kg rest on a horizontal plane . The plane is gradually inclined until an angle 0=15∘ with the horizontal and the mass just begins to slide . What is the coefficient of static friction between the block and the surface ?
View Solution
Knowledge Check
A block of mass 3 kg rests on a rough inclined plane making an angle of 30∘. With the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
A9.8 NB0.7×9.8×√3 NC9.8×√3 ND0.7×9.8 NA block of mass 2kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
A10.3NB23.8NC11.9ND6.3N
A block of mass 4kg rests on a rough horizontal plane. The plane is gradually inclined until at an angle θ=60∘ , with the vertical, the mass just begins to side. What is the coefficient of static friction between the block and the plane?
View SolutionA block of mass 8 kg is sliding on a surface inclined at an angle of 45∘ with the horizontal . Calculate the acceleration of the block . The coefficient of friction between the block and surface is 0⋅6 ( Take g = 10m/s2)
View SolutionA block of mass 2kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
View SolutionA block of mass 2 kg rests on a rough inclined plane making an angle of 30° with the horizontal. If μS=0.6 , what is the frictional force on the block ?
View SolutionA block of mass 8 kg is sliding on a surface inclined at an angle of 45∘ with the horizontal. Calculate the acceleration of the block. The coefficient of friction between the block and surface is 0.6. (Take g=10m/s2)
View SolutionA block rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.8. If the frictional force on the block is 10N, the mass of the block (in kg) is
View Solution
