Question

A particle is moving on a circular path with constant speed v. The magnitude of the change in its velocity after it has described an angle of ${\displaystyle {90}^{\circ }}$ is :

Options

A. v
B. `sqrt(2) v`
C. 0
D. `sqrt(3)` v

Answer

b

Explanation

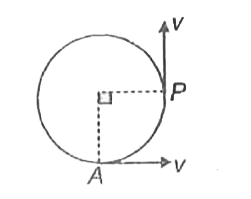
To solve the problem of finding the magnitude of the change in velocity of a particle moving in a circular path after it has described an angle of 90 degrees, we can follow these steps:

1. Understanding Initial and Final Velocity:
- The particle is moving with a constant speed \( v \) in a circular path.
- At the initial position, let's assume the particle is at point A, moving along the positive x-axis. Thus, the initial velocity vector \( \vec{V_i} \) can be represented as:
\( \vec{V_i} = v \hat{i} \)
- After moving through an angle of 90 degrees, the particle will be at point B, moving along the positive y-axis. Therefore, the final velocity vector \( \vec{V_f} \) can be represented as:
\( \vec{V_f} = v \hat{j} \)

2. Calculating Change in Velocity:
- The change in velocity \( \Delta \vec{V} \) is given by:
\( \Delta \vec{V} = \vec{V_f} - \vec{V_i} \)
- Substituting the values of \( \vec{V_f} \) and \( \vec{V_i} \):
\( \Delta \vec{V} = v \hat{j} - v \hat{i} \)
- This can be rewritten as:
\( \Delta \vec{V} = -v \hat{i} + v \hat{j} \)

3. Finding the Magnitude of Change in Velocity:
- The magnitude of the change in velocity \( |\Delta \vec{V}| \) can be calculated using the Pythagorean theorem:
\( |\Delta \vec{V}| = \sqrt{(-v)^2 + (v)^2} \)
- Simplifying this:
\( |\Delta \vec{V}| = \sqrt{v^2 + v^2} = \sqrt{2v^2} = v\sqrt{2} \)

4. Conclusion:
- Therefore, the magnitude of the change in velocity after the particle has described an angle of 90 degrees is:
\( |\Delta \vec{V}| = \sqrt{2}v \)

Final Answer:
The magnitude of the change in velocity is \( \sqrt{2}v \).

---