A car is moving in a circular path with a uniform speed v. Find the magnitude of change in its velocity when the car rotates through an angle θ.
To find the magnitude of the change in velocity of a car moving in a circular path with uniform speed v after it rotates through an angle θ, we can follow these steps:
Step 1: Understand the Initial and Final Velocity Vectors
- Initially, the car is moving in a direction tangent to the circular path. We can represent this initial velocity vector as:
vinitial=v^j
(assuming the car is moving in the positive y-direction).
- After rotating through an angle θ, the final velocity vector will be at an angle θ to the initial direction. We can break this down into components:
vfinal=vcos(θ)^j−vsin(θ)^i
Step 2: Calculate the Change in Velocity
- The change in velocity Δv can be calculated as:
Δv=vfinal−vinitial
Substituting the expressions for vfinal and vinitial:
Δv=(−vsin(θ)^i+vcos(θ)^j)−(0^i+v^j)
Simplifying this gives:
Δv=−vsin(θ)^i+(vcos(θ)−v)^j
Δv=−vsin(θ)^i+v(cos(θ)−1)^j
Step 3: Calculate the Magnitude of the Change in Velocity
- The magnitude of the change in velocity |Δv| can be calculated using the Pythagorean theorem:
|Δv|=√(−vsin(θ))2+(v(cos(θ)−1))2
=√v2sin2(θ)+v2(cos(θ)−1)2
=v√sin2(θ)+(cos(θ)−1)2
Step 4: Simplify the Expression
- Now, we simplify (cos(θ)−1)2:
(cos(θ)−1)2=cos2(θ)−2cos(θ)+1
Therefore:
|Δv|=v√sin2(θ)+cos2(θ)−2cos(θ)+1
Using the identity sin2(θ)+cos2(θ)=1:
|Δv|=v√2−2cos(θ)=v√2(1−cos(θ))
Using the identity 1−cos(θ)=2sin2(θ2):
|Δv|=v√4sin2(θ2)=2vsin(θ2)
Final Answer
The magnitude of the change in velocity when the car rotates through an angle θ is:
|Δv|=2vsin(θ2)
- Initially, the car is moving in a direction tangent to the circular path. We can represent this initial velocity vector as:
vinitial=v^j
(assuming the car is moving in the positive y-direction).
vfinal=vcos(θ)^j−vsin(θ)^i
- The change in velocity Δv can be calculated as:
Δv=vfinal−vinitial
Substituting the expressions for vfinal and vinitial:
Δv=(−vsin(θ)^i+vcos(θ)^j)−(0^i+v^j)
Simplifying this gives:
Δv=−vsin(θ)^i+(vcos(θ)−v)^j
Δv=−vsin(θ)^i+v(cos(θ)−1)^j
- The magnitude of the change in velocity |Δv| can be calculated using the Pythagorean theorem:
|Δv|=√(−vsin(θ))2+(v(cos(θ)−1))2
=√v2sin2(θ)+v2(cos(θ)−1)2
=v√sin2(θ)+(cos(θ)−1)2
- Now, we simplify (cos(θ)−1)2:
(cos(θ)−1)2=cos2(θ)−2cos(θ)+1
Therefore:
|Δv|=v√sin2(θ)+cos2(θ)−2cos(θ)+1
Using the identity sin2(θ)+cos2(θ)=1:
|Δv|=v√2−2cos(θ)=v√2(1−cos(θ))
Using the identity 1−cos(θ)=2sin2(θ2):
|Δv|=v√4sin2(θ2)=2vsin(θ2)
The magnitude of the change in velocity when the car rotates through an angle θ is:
|Δv|=2vsin(θ2)
Topper's Solved these Questions
- MOTION IN A PLANEBook:AAKASH SERIESChapter:MOTION IN A PLANEExercise:SHORT ANSWER TYPE QUESTIONS
Explore 6 Videos
- MOTION IN A PLANEBook:AAKASH SERIESChapter:MOTION IN A PLANEExercise:VERY SHORT ANSWER TYPE QUESTIONS
Explore 10 Videos
- MOTION IN A PLANEBook:AAKASH SERIESChapter:MOTION IN A PLANEExercise:EXERCISE-3 (Circular Motion)
Explore 7 Videos
- MOTION IN A STRAIGHT LINE Book:AAKASH SERIESChapter:MOTION IN A STRAIGHT LINE Exercise:very Short answer type question
Explore 15 Videos
Similar Questions
Knowledge Check
A particle is moving on a circular path with a constant speed v. Its change of velocity as it moves from A to B is:
 A2vsin(2θ)BzeroC2vsin(θ2)D2vcos(θ2)
A2vsin(2θ)BzeroC2vsin(θ2)D2vcos(θ2)
A particle is moving along a circular path with a constant speed 10ms−1.What is the magnitude of the change in velocity of the particle ,when it moves through an angle of 60∘ around the center of the circle ?
View SolutionA particle is moving on a circular path with constant speed v then the change in its velocity after it has described an angle of 60∘ will be
View SolutionA particle of mass 2 kg is moving in circular path with constant speed 20 m/s. The magnitude of change in velocity when particle travels from A to P will be
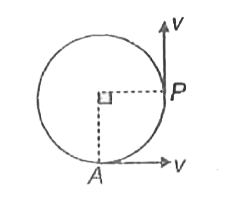
View SolutionA particle is moving on a circular path of radius 10m with uniform speed of 4ms−1.The magnitude of change in velocity of particle when it completes a semi circular path is
View SolutionA particle is moving along a circular path with uniform speed. Through what angle does its angular velocity change when it completes half of the circular path ?
View Solution
A particle is moving on a circular path of radius r with uniform velocity v. The change in velocity when the particle moves from P to Q is (∠POQ=40∘)
View SolutionA particle of mass m is moving on a circular path of radius r with uniform speed v , rate of change of linear momentum is
View Solution

