Four small objects each of mass m are fixed at the corners of a rectangular wire-frame of negligible mass and of sides a and b (a > b) . If the wire frame is now rotated about an axis passing along the side of length then the moment of inertia of the system for this axis of rotation is:
2ma2
4ma2
2m(a2+b2)
2m(a2−b2)
The correct Answer is:A
To find the moment of inertia of the system consisting of four small objects each of mass m fixed at the corners of a rectangular wire-frame with sides a and b (where a>b), and rotating about an axis along the side of length b, we can follow these steps:
1. Identify the Configuration:
- We have a rectangle with corners at (0,0), (a,0), (0,b), and (a,b).
- The axis of rotation is along the side of length b, which we can assume is along the line x=0 (the left vertical side of the rectangle).
2. Determine the Positions of the Masses:
- The positions of the masses are:
- Mass at (0,0): This mass is on the axis of rotation.
- Mass at (a,0): This mass is also on the axis of rotation.
- Mass at (0,b): This mass is at a distance b from the axis of rotation.
- Mass at (a,b): This mass is at a distance b from the axis of rotation.
3. Calculate the Moment of Inertia Contributions:
- The moment of inertia I is given by the formula:
I=∑mir2i
- For the mass at (0,0):
I1=m⋅02=0
- For the mass at (a,0):
I2=m⋅02=0
- For the mass at (0,b):
I3=m⋅b2
- For the mass at (a,b):
I4=m⋅b2
4. Sum the Contributions:
- Now, sum all the contributions to find the total moment of inertia:
I=I1+I2+I3+I4=0+0+mb2+mb2=2mb2
5. Final Moment of Inertia:
- Since we are rotating about the side of length b, we need to consider the distance of the masses from the axis of rotation. The total moment of inertia about the axis along side b is:
I=2m⋅a2
- Therefore, the final answer is:
I=2ma2
Conclusion:
The moment of inertia of the system about the axis passing along the side of length b is 2ma2.
- We have a rectangle with corners at (0,0), (a,0), (0,b), and (a,b).
- The axis of rotation is along the side of length b, which we can assume is along the line x=0 (the left vertical side of the rectangle).
- The positions of the masses are:
- Mass at (0,0): This mass is on the axis of rotation.
- Mass at (a,0): This mass is also on the axis of rotation.
- Mass at (0,b): This mass is at a distance b from the axis of rotation.
- Mass at (a,b): This mass is at a distance b from the axis of rotation.
- The moment of inertia I is given by the formula:
I=∑mir2i
- For the mass at (0,0):
I1=m⋅02=0
- For the mass at (a,0):
I2=m⋅02=0
- For the mass at (0,b):
I3=m⋅b2
- For the mass at (a,b):
I4=m⋅b2
- Now, sum all the contributions to find the total moment of inertia:
I=I1+I2+I3+I4=0+0+mb2+mb2=2mb2
- Since we are rotating about the side of length b, we need to consider the distance of the masses from the axis of rotation. The total moment of inertia about the axis along side b is:
I=2m⋅a2
- Therefore, the final answer is:
I=2ma2
The moment of inertia of the system about the axis passing along the side of length b is 2ma2.
Topper's Solved these Questions
Similar Questions
Two identical rings each of mass m with their planes mutually perpendicular, radius R are welded at their point of contact O. If the system is free to rotate about an axis passing through the point P perpendicular to the plane of the paper, then the moment of in inertia of the system about this axis is equal to

View SolutionA square frame is made rods each of mass m and length l. The moment of inertia of the square about its face diagonal is
View Solution
Knowledge Check
Three point masses each of mass m are placed at the corners of an equilateral triangle of side b. The moment of inertia of the system about an axis coinciding with one side of the triangle is
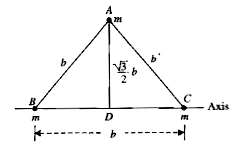 A3mb2Bmb2C(3/4)mb2D(2/3)mb2
A3mb2Bmb2C(3/4)mb2D(2/3)mb2
Five particles of mass 2 kg are attached to the rim of a circular disc of radius 0.1 m & negligible mass. Moment of inertia of the system about an axis passing through the centre of the disc & perpendicular to its plane is
View SolutionFour point masses, each of mass m, are fixed at the corners of a square of side l. The square is rotating with angular frequency ω, about an axis passing through one of the corners of the square and parallel to its diagonal , as shown. Angular momentum about this axis is :

View SolutionFour particle of mass m each are placed at four corners of a square ABCD of side a. Point O is the centre of the square. Moment of inertia of all four particles about an axis passing through
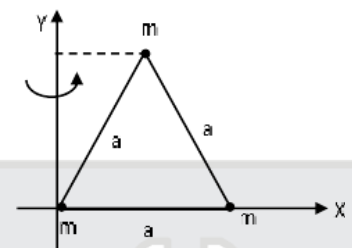
View SolutionIn the diagram three point masses 'm' each are fixed at the corners of an equilateral triangle.Moment of inertia of the system abouty-axis is N10ma2, N is:
View SolutionTwo balls of masses m and 2m are attached to the ends of a light rod of length L. The rod rotates with an angular speed ω about an axis passing through the center of mass of system and perpendicular to the plane. Find the angular momentum of the system about the axis of rotation.
View SolutionThree thin rods each of length Land mass M are placed along x, y and z-axes such that one end of each rod is at origin. The moment of inertia of this system about z-axis is
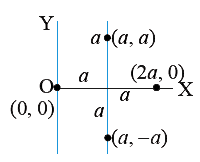
View SolutionFour point masses (each of mass m) are arranged it the X-Y plane the moment of inertia of this array of masses about Y-axis is
View Solution

