A body executes SHM under the influence of one force and has a period T1 seconds and the same body executes SHM with period T2 seconds when under the influence of another force. When both forces act simultaneously and in the same direction, then the time period of the same body (in seconds) is:
T1+T2
√T21+T22
√T21+T22T1T2
⎷T21T22(T21+T22)
The correct Answer is:D
To solve the problem, we need to find the time period of a body executing Simple Harmonic Motion (SHM) when two forces act on it simultaneously. Here’s the step-by-step solution:
Step 1: Understand the Forces Acting on the Body
When a body is under the influence of two forces, the forces can be represented as:
- Force 1: F1=k1x
- Force 2: F2=k2x
Where k1 and k2 are the force constants for each force, and x is the displacement from the mean position.
Step 2: Determine the Time Periods for Each Force
The time period T of a body executing SHM is given by the formula:
T=2π√mk
Where m is the mass of the body and k is the effective spring constant.
For the first force:
T1=2π√mk1
For the second force:
T2=2π√mk2
Step 3: Express the Spring Constants in Terms of Time Periods
Rearranging the formulas for k1 and k2:
k1=4π2mT21
k2=4π2mT22
Step 4: Find the Effective Spring Constant When Both Forces Act
When both forces act simultaneously, the effective spring constant knet is the sum of the individual spring constants:
knet=k1+k2
Substituting the expressions for k1 and k2:
knet=4π2mT21+4π2mT22
Step 5: Calculate the Time Period for the Combined System
Now, using the effective spring constant to find the new time period Tnet:
Tnet=2π√mknet
Substituting for knet:
Tnet=2π
⎷m4π2mT21+4π2mT22
This simplifies to:
Tnet=2π
⎷m4π2m(1T21+1T22)
The mass m cancels out:
Tnet=2π
⎷14π2(1T21+1T22)
Tnet=
⎷T21T22T21+T22
Final Result
Thus, the time period when both forces act simultaneously is:
Tnet=
⎷T21T22T21+T22
When a body is under the influence of two forces, the forces can be represented as:
- Force 1: F1=k1x
- Force 2: F2=k2x
The time period T of a body executing SHM is given by the formula:
T=2π√mk
Where m is the mass of the body and k is the effective spring constant.
T1=2π√mk1
For the second force:
T2=2π√mk2
Rearranging the formulas for k1 and k2:
k1=4π2mT21
k2=4π2mT22
When both forces act simultaneously, the effective spring constant knet is the sum of the individual spring constants:
knet=k1+k2
knet=4π2mT21+4π2mT22
Now, using the effective spring constant to find the new time period Tnet:
Tnet=2π√mknet
Substituting for knet:
Tnet=2π
⎷m4π2mT21+4π2mT22
This simplifies to:
Tnet=2π
⎷m4π2m(1T21+1T22)
The mass m cancels out:
Tnet=2π
⎷14π2(1T21+1T22)
Tnet=
⎷T21T22T21+T22
Thus, the time period when both forces act simultaneously is:
Tnet=
⎷T21T22T21+T22
Topper's Solved these Questions
Similar Questions
A body executes simple harmonic motion under the action of a force F1 with a time period 45s . If the force is changed to F2, it executes SHM with time period 35s. If both the forces F1andF2 act simultaneously in the same direction on the body, its time period (in seconds) is
View SolutionA particle has a time period of 1s under the action of a certain force and 2 s under the action of another force. Find the time period when the forces are acting in the same direction simultaneously.
View Solution
Knowledge Check
When a body vibrates under a periodic force, the vibrations of the body are :
Anatural vibrationsBdamped vibrationsCforced vibrationsDresonant vibrations.
A particle under the action of a force has a period of 3s and under the action of another force it has a period 4sec in SHM. What will be its period under the combined action of both forces in the same direction?
View SolutionA body has a time of 3 s under the action of one force and 4 s under the action of another force. Calculate the time period when both the forces act in the same direction simultaneously. Assume that the body undergoes the same displacement, under the action of the two different forces.
View SolutionA body is in equilibrium under the influence of a number of forces. Each has a different line of action. The minimum number of forces required is.
View SolutionA body of mass 0.01 kg executes simple harmonic motion (SHM) about x=0 under the influence of a force shown in the figure. The period of the SHM is
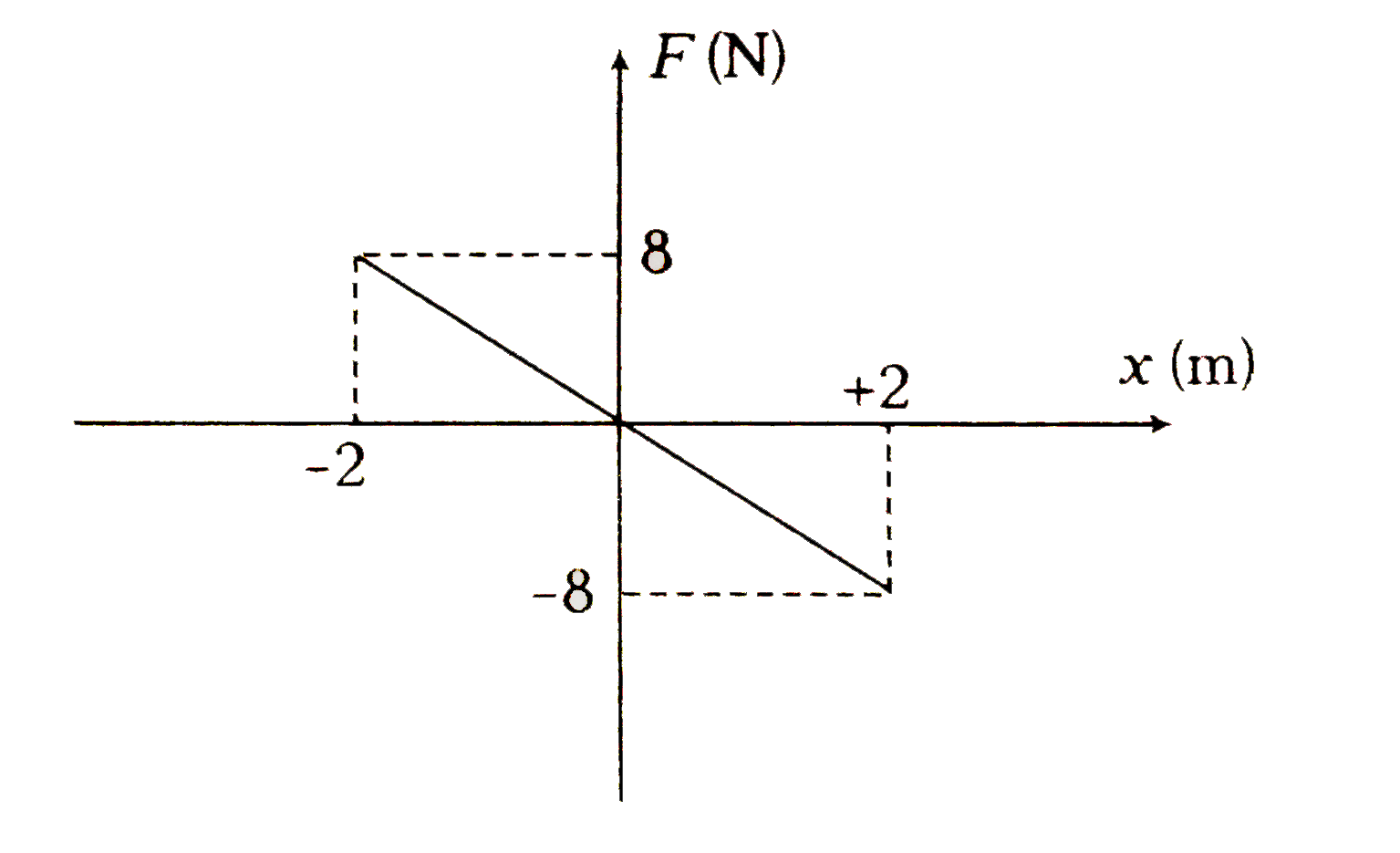
View SolutionA particle under the action of one SHM has a period of 3 s and under the effect of another it has a period 4s. Its time period under the combined action of both the SHM's in the same direction is (0.4x)second. Find value of x?
View SolutionA body is executing S.H.M. when its displacement from the mean position is 4 cm and 5 cm, the corresponding velocity of the body is 10 cm/sec and 8 cm/sec. Then the time period of the body is
View SolutionA body of mass m has time period T1 with one spring and has time period T2 with another spring. If both the springs are connected in parallel and same mass is used, then new time period T is given as
View Solution
