In YDSE with d=1mm and D=1m, Slabs of (t=1μm,μ=3) and (t=0.5μm,μ=2) are introduced in front of upper and lower slits, respectively. Find the shift in the fringe pattern.
Optical path for light coming from upper slit S1 is
S1P+1μ,(2−1)=S2+0.5μm
Similarly optical path for light coming from S2 is
S1P+0.5μ,(2−1)=S2+0.5μm
Path difference : Δp=(S2P+0.5μm)−(S1P+2μm)=(S2P−S1P)−1.5μm.
=ydD−1.5μm
for central bright fringe Δp=0
⇒y=1.5μm1mm×1m=1.5mm.
The whole pattern is shifted by 1.5mm upwards.
Topper's Solved these Questions
Similar Questions
In YDSE, let A and B be two slits. Films of thickness tA and tB and refractive μA and μB are placed in front of A and B, respectively. If μAtA=μAtB, then the central maxima will
View SolutionA monochromatic beam of light falls on YDSE apparatus at some angle (θ) as shown, a thin sheet of glas (R.I. = μ, thickness = t) is insdted in front of the lower slit S2. Select the correct alternative.

View SolutionFigure shows a YDSE setup having identical slits S1 and S2 with d =5 mm and D = 1 m. A monochromatic light of wavelength λ=6000Å is incident on the plane of slit due to which at screen centre O, an intensity I0 is produced with fringe pattern on both sides Now a thin transparent film of 11μm thickness and refractive index μ=2.1 is placed in front of slit S1 and now interference patten is observed again on screen.
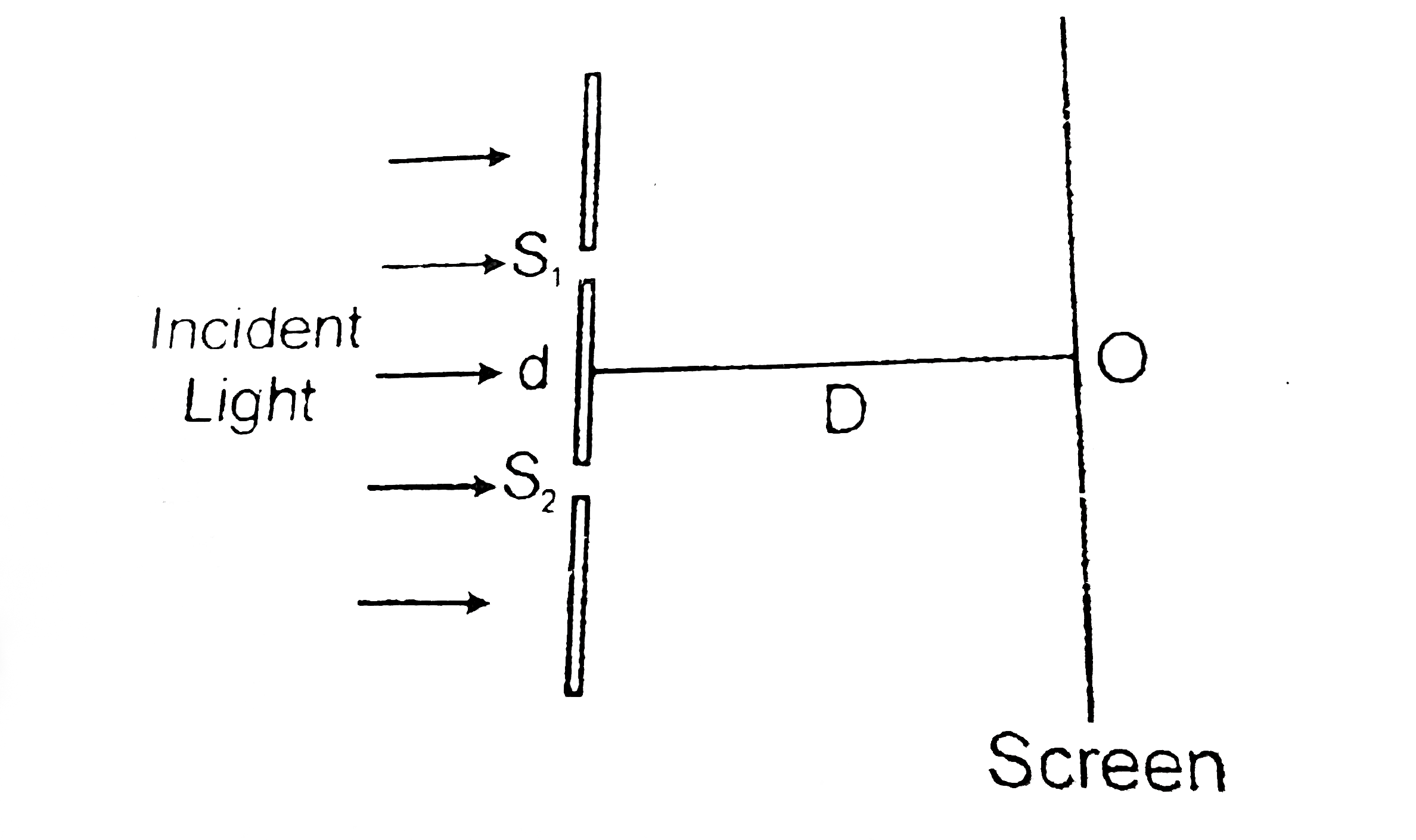
Due to placement of film in front of S1, how many bright fringes cross the point O of screen excluding the one which was at O earlier :
View SolutionFigure shows a YDSE setup having identical slits S1 and S2 with d =5 mm and D = 1 m. A monochromatic light of wavelength λ=6000Å is incident on the plane of slit due to which at screen centre O, an intensity I0 is produced with fringe pattern on both sides Now a thin transparent film of 11μm thickness and refractive index μ=2.1 is placed in front of slit S1 and now interference patten is observed again on screen.
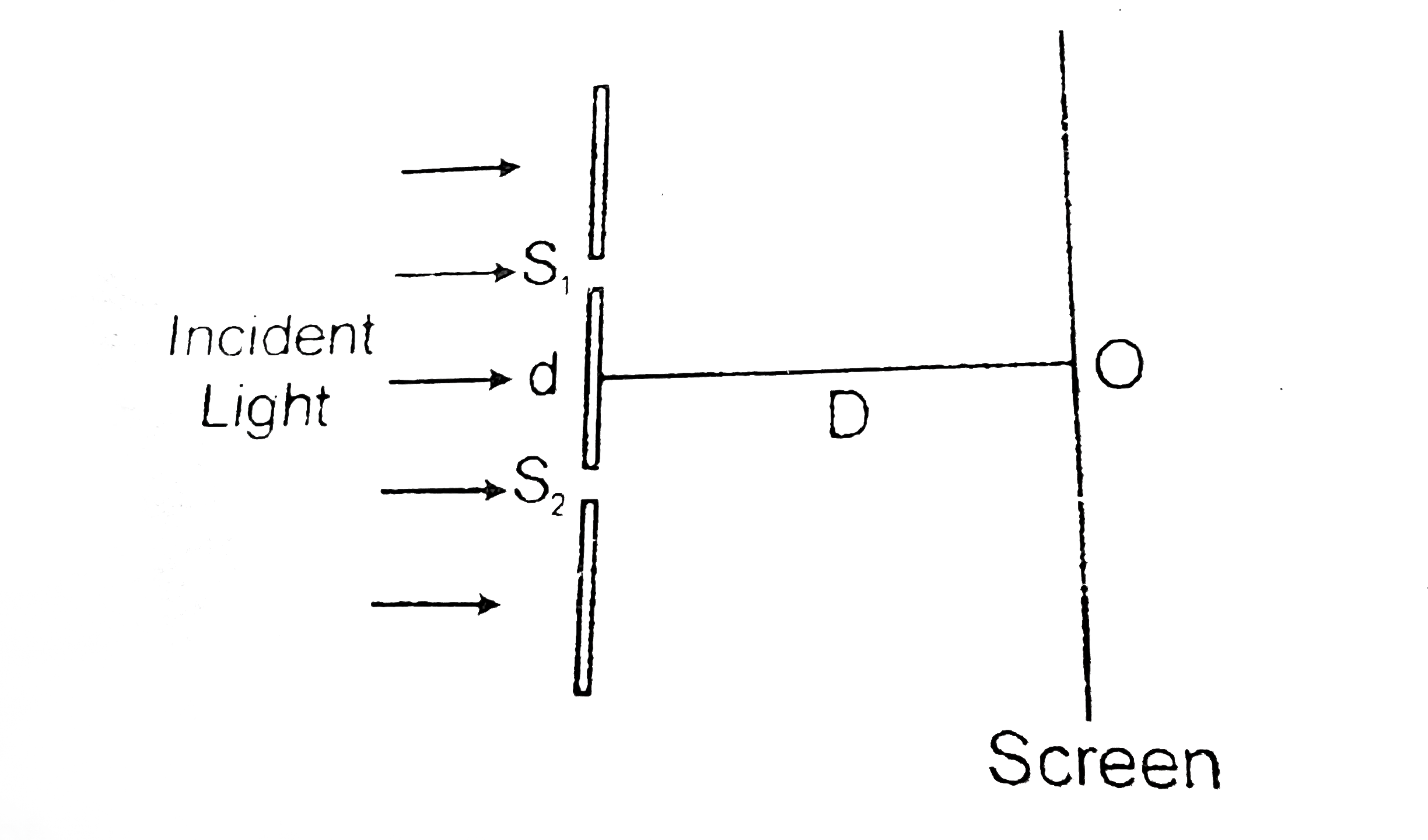
After placing the film of slit S1, the intensity at point O screen is :
View SolutionFigure shows a YDSE setup having identical slits S1 and S2 with d =5 mm and D = 1 m. A monochromatic light of wavelength λ=6000Å is incident on the plane of slit due to which at screen centre O, an intensity I0 is produced with fringe pattern on both sides Now a thin transparent film of 11μm thickness and refractive index μ=2.1 is placed in front of slit S1 and now interference patten is observed again on screen.

After placing the film of slit S1, the intensity at point O screen is :
View SolutionIn a modified YDSE, the region between the screen and slits is immersed in a liquid whose refractive index varies with time as μ1=(5/2)−(T/4) until it reaches s steady state value of 5/4. A glass plate of thickness 36 μm and refractive index 3/2 is introduced in front of one of the slits.
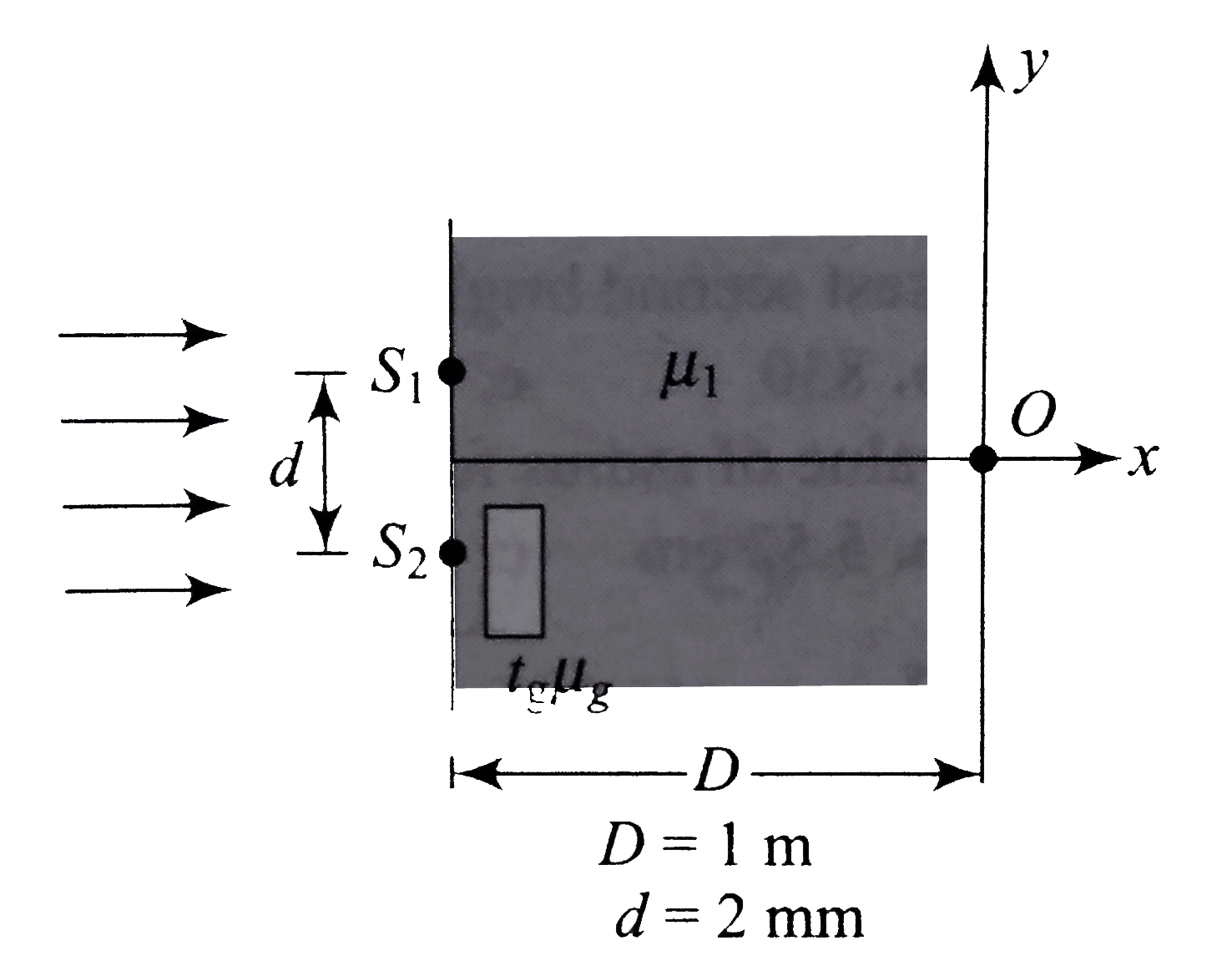
Find the time when central maxima is at point O. located symmetrically on the x-asix.
View SolutionIn a doulble slit experiment when a thin film of thickness t having refractive index μ is introduced in from of one of the slits, the maximum at the centre of the fringe pattern shifts by one width. The value of t is (λ is the wavelength of the light used)
View SolutionIn Young's double slit experiment S1 and S2 are two slits. Films of thickness t1 and t2 and refractive indices μ1 and μ2 are placed in front of S1 and S2 respectively. If μ1t1=μ2t2, then the central maximum will :
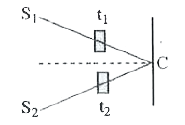
View SolutionIn a modified YDSE, the region between the screen and slits is immersed in a liquid whose refractive index varies with time as μ1=(5/2)−(T/4) until it reaches s steady state value of 5/4. A glass plate of thickness 36 μm and refractive index 3/2 is introduced in front of one of the slits.

What is the speed of the central maxima when it is at
View SolutionA glass slab (μ=1.5) of thickness 6 cm is placed over a paper. What is the shift in the letters?
View Solution
