Two converging lenses of the same focal length f are separated by a distance 2f. The axis of the second lens is inclined at angle θ=60∘ with respect to the axis of the first lens. A parallel paraxial beam of light is incident from left side of the lens. Find the coordinates of the final image with respect to the origin of the first lens.
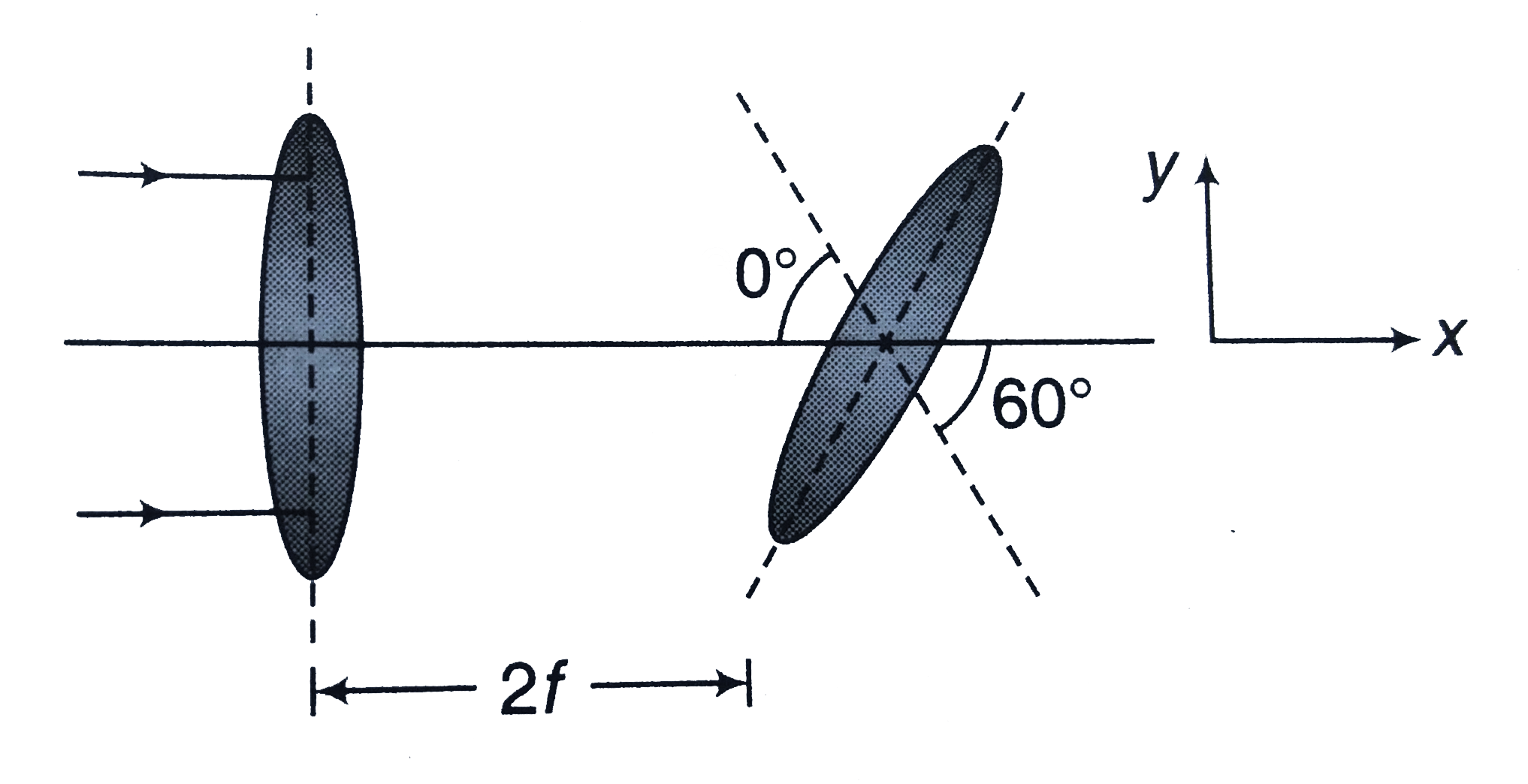
The correct Answer is:f(1−2cosθ)1−cosθ,0
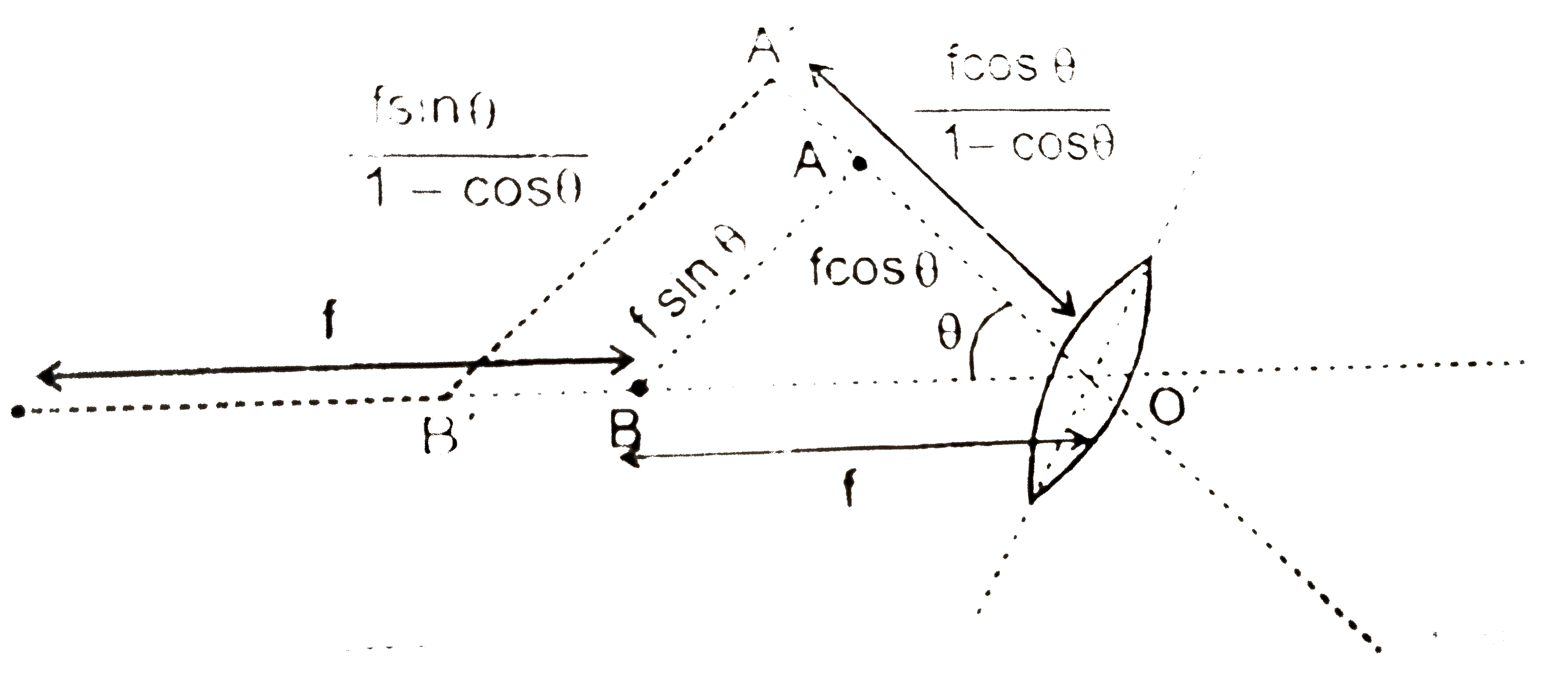
1v−1u=1f
1v−1−fcosθ=1f
v=fcosθcos−1=−fcosθ(1−cosθ)
m=vu=fcosθ/[cosθ−1]−fcosθ⇒m=(11−cosθ)
∴A'B'AB=(fcosθ1−cosθ)/fcosθ
⇒A'B'=fsinθ1−cosθ
From similar triangles, B' lies on the principal axis of first lens.
∴y=o and x=2f−O'B'=2f−f(1−cosθ)=f(1−2cosθ)(1−cosθ)

Topper's Solved these Questions
Similar Questions
Find the focal length of the lens shwon in figure
(a) If the light is incident form left side.
(b) If the light is incident form right side.

View SolutionIf the optic axis of convex and concave lenses are separated by a distance 5mm as shown in the figure. Find the coordinate of the final image formed by the combination if parallel beam of light is incident on lens. Origin is at the optical centre of convex lens

View SolutionA parallel beam of light is incident on a lens of focal length 10 cm. A parallel slab of refractive index 1.5 and thickness 3 cm is placed on the other side of the lens. Find the distance of the final image from the lens.
 .
.
View SolutionTwo converging lenses of focal lengths f1=10cm and f2=20cm are placed at some separation. A parallel beam of light is incident on first lens. Then,
View SolutionA glass wedge with a small angle of refraction θ is placed at a certain distance from a converging lens with a focal length f ,one surface of the wedge being perpendicular to the optical axis of the lens. A point sources S of light is on the other side of the lens at its focus. The rays reflected from the wedge (not from base) produce, after refraction in the lens , two images of the source displaced with respect to each other by d. Find the refractive index of the wedge glass. [Consider only paraxial rays.]
_E01_162_Q01.png)
View SolutionTwo thin convex lenses of focal lengths f1 and f2 are separated by a horizontal distance d (whered<f1,d<f2) and their centres are displaced by a vertical separation △ as shown in the fig.
Taking the origin of coordinates O, at the centre of the first lens the x and y coordinates of the focal point of this lens system, for a parallel beam of rays coming form the left, are given by:
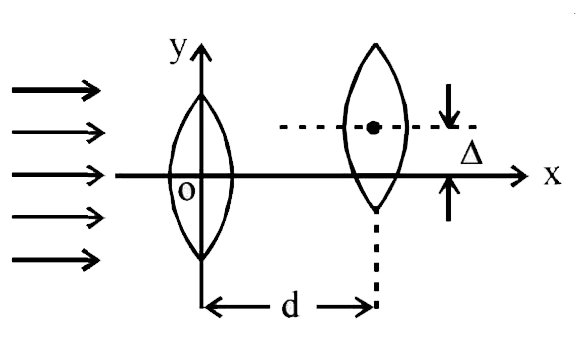
View SolutionTwo thin convex lenses of focal lengths f1 and f2 are separated by a horizontal distance d (whered<f1,d<f2) and their centres are displaced by a vertical separation △ as shown in the fig.
Taking the origin of coordinates O, at the centre of the first lens the x and y coordinates of the focal point of this lens system, for a parallel beam of rays coming form the left, are given by:
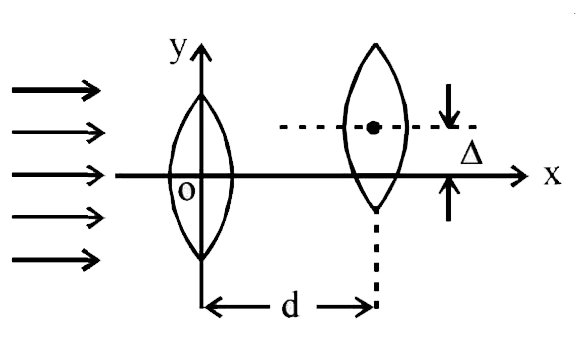
View SolutionA beam of parallel rays is brought to focus by a planoconvex lens. A thin Concave lens of the same focal length is joined to the first lens. The effect of this is
View SolutionAn object is placed at a distance of 10cm to the left on the axis of convex lens A of focal length 20cm. A second convex lens of focal length 10cm is placed coaxially to the right of the lens A at a distance of 5cm from A. Find the position of the final image and its magnification. Trace the path of the rays.
View SolutionA convex lens of focal length 1.0m and a concave lens of focal length 0.25m are 0.75m apart. A parallel beam of light is incident on the convex lens. The beam emerging after refraction from both lenses is
View Solution
