A kid of height 1.1ft is sleeping straight between focus and centre of curvature along the principal axis of a concave mirror of small aperture. His head is towards the mirror and is 0.5ft from the focus of the mirror. How a plane mirror should be placed so that the image formed by it due to reflected light from concave mirror looks like a person of height 5.5ft standing vertically. Draw the ray diagram. Find the focal length of the concave mirror.
The correct Answer is:The plane mirror should be placed at an angel of 45∘ with negative x−axis;f=2ft.
(##RESOPTPHYXIIC01E01230_A01##)
To solve the problem step by step, we will follow the given information and apply the principles of geometrical optics.
Step 1: Understand the Setup
We have a concave mirror with a kid lying between the focus (F) and the center of curvature (C). The kid's height is 1.1 ft, and his head is 0.5 ft from the focus. We need to determine how to place a plane mirror so that the image formed looks like a person of height 5.5 ft.
Step 2: Determine the Positions
- The distance from the focus (F) to the kid's head (B) is 0.5 ft.
- The distance from the focus (F) to the kid's feet (A) can be calculated as:
Distance from F to A=1.1 ft (height of the kid)+0.5 ft=1.6 ft
Step 3: Use the Mirror Formula
The mirror formula is given by:
1f=1v+1u
Where:
- f = focal length of the mirror
- v = image distance
- u = object distance (negative for concave mirror)
For the head (B):
- Object distance uB=−0.5 ft (from F to B)
- Let vB be the image distance for B.
Using the mirror formula:
1f=1vB+1−0.5
For the feet (A):
- Object distance uA=−1.6 ft (from F to A)
- Let vA be the image distance for A.
Using the mirror formula:
1f=1vA+1−1.6
Step 4: Relate the Image Heights
The height of the image formed by the concave mirror will be related to the height of the kid. The height of the image (h') is given by:
h′h=vu
Where h is the height of the object (1.1 ft), and h′ is the height of the image.
For the plane mirror, the image height will be the same as the height of the object reflected in it. We want the total height of the image (reflected) to be 5.5 ft.
Step 5: Set Up the Equation
We know that:
h′=vB−0.5⋅1.1
And for the feet:
h′=vA−1.6⋅1.1
We want the difference in heights to equal 5.5 ft:
|vB−vA|=5.5
Step 6: Solve for Focal Length
From the previous equations, we can solve for vB and vA in terms of f:
1. Rearranging the equations gives us expressions for vB and vA.
2. Set the difference equal to 5.5 ft and solve for f.
Step 7: Calculate Focal Length
After substituting and simplifying, we find:
f=2 ft
Step 8: Draw the Ray Diagram
1. Draw the concave mirror with the principal axis.
2. Mark the focus (F) and center of curvature (C).
3. Draw the object (the kid) between F and C.
4. Draw rays from the object to the mirror:
- One ray parallel to the principal axis reflecting through the focus.
- Another ray passing through the focus reflecting parallel to the principal axis.
5. Extend these rays to find the image location.
Final Answer
- The focal length of the concave mirror is 2 ft.
- The placement of the plane mirror should be such that it reflects the image to appear as a height of 5.5 ft.
We have a concave mirror with a kid lying between the focus (F) and the center of curvature (C). The kid's height is 1.1 ft, and his head is 0.5 ft from the focus. We need to determine how to place a plane mirror so that the image formed looks like a person of height 5.5 ft.
- The distance from the focus (F) to the kid's head (B) is 0.5 ft.
- The distance from the focus (F) to the kid's feet (A) can be calculated as:
Distance from F to A=1.1 ft (height of the kid)+0.5 ft=1.6 ft
The mirror formula is given by:
1f=1v+1u
Where:
- f = focal length of the mirror
- v = image distance
- u = object distance (negative for concave mirror)
- Object distance uB=−0.5 ft (from F to B)
- Let vB be the image distance for B.
1f=1vB+1−0.5
- Object distance uA=−1.6 ft (from F to A)
- Let vA be the image distance for A.
1f=1vA+1−1.6
The height of the image formed by the concave mirror will be related to the height of the kid. The height of the image (h') is given by:
h′h=vu
Where h is the height of the object (1.1 ft), and h′ is the height of the image.
We know that:
h′=vB−0.5⋅1.1
And for the feet:
h′=vA−1.6⋅1.1
We want the difference in heights to equal 5.5 ft:
|vB−vA|=5.5
From the previous equations, we can solve for vB and vA in terms of f:
1. Rearranging the equations gives us expressions for vB and vA.
2. Set the difference equal to 5.5 ft and solve for f.
After substituting and simplifying, we find:
f=2 ft
1. Draw the concave mirror with the principal axis.
2. Mark the focus (F) and center of curvature (C).
3. Draw the object (the kid) between F and C.
4. Draw rays from the object to the mirror:
- One ray parallel to the principal axis reflecting through the focus.
- Another ray passing through the focus reflecting parallel to the principal axis.
5. Extend these rays to find the image location.
- The focal length of the concave mirror is 2 ft.
- The placement of the plane mirror should be such that it reflects the image to appear as a height of 5.5 ft.
Topper's Solved these Questions
- GEOMATRICAL OPTICS Book:RESONANCE ENGLISHChapter:GEOMATRICAL OPTICS Exercise:Exercise-3
Explore 80 Videos
- EXPERIMENTAL PHYSICSBook:RESONANCE ENGLISHChapter:EXPERIMENTAL PHYSICSExercise:PART -II
Explore 10 Videos
- GRAVITATIONBook:RESONANCE ENGLISHChapter:GRAVITATIONExercise:HIGH LEVEL PROBLEMS
Explore 16 Videos
Similar Questions
Knowledge Check
An object is kept on the principal axis of a concave mirror of focal length 10cm, at a distance of 15 cm from its pole. The image formed by the mirror is:
AVirtual and magnifiedBVirtual and diminishedCReal and magnifiedDReal and diminished
The image formed by a concave mirror
View SolutionAn object is between the principal focus and the centre of curvature of a concave mirror. The image formed is real and :
View SolutionA concave mirror forms a virtual image of size twice that of the object placed at a distance 5 cm from it . Find the focal length of the mirror.
View SolutionAn object is present on the principal axis of a concave mirror at a distance 30cm from it. Focal length of mirror is 20cm.
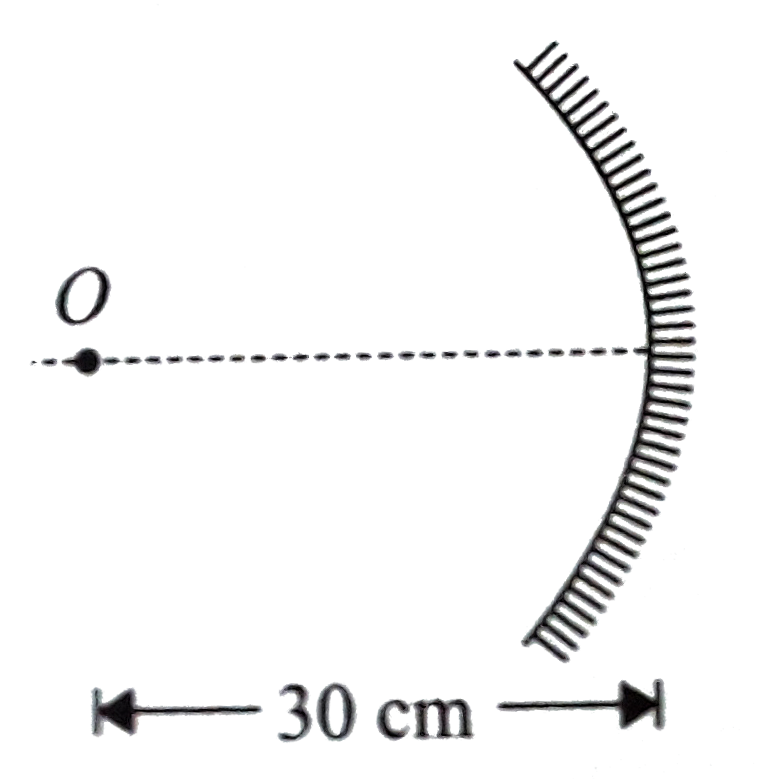
Q. Image formed by mirror is
View SolutionA parallel beam of light, parallel to the principal axis of a concave mirror, on reflection meets at the :
View SolutionAn object is placed in front of a concave mirror between the pole and the focus of the mirror. What is the nature of the image formed by the mirror ?
View SolutionImage formed by reflection from a plane mirror is :
View Solution

