A beam of parallel rays of diameter 'b' propagates in glass at an angle θ to its plane. Find the diameter of the beam when it goes to air through this face. (nglass=n)
The correct Answer is:CD=d√1−n2cos2θsinθ
To solve the problem of finding the diameter of a beam of parallel rays when it propagates from glass to air, we can follow these steps:
1. Understanding the Setup:
- We have a beam of parallel rays of diameter b propagating in glass with a refractive index n at an angle θ to the normal of the surface.
2. Identify the Angles:
- The angle of incidence i is given as θ.
- According to Snell's law, the relationship between the angles and the refractive indices is given by:
nsin(i)=sin(r)
- Here, r is the angle of refraction when the beam exits into air (where the refractive index is approximately 1).
3. Using Snell's Law:
- From Snell's law, we can express:
nsin(θ)=sin(r)
- This implies:
sin(r)=nsin(θ)
4. Finding the Diameter After Refraction:
- The diameter of the beam after refraction can be expressed in terms of the original diameter and the angles involved.
- For the triangle formed by the rays, we can use the cosine of the angle of refraction:
CD=AB⋅cos(r)
- Since AB=b, we have:
CD=b⋅cos(r)
5. Relating cos(r) to θ:
- We can find cos(r) using the identity:
cos2(r)=1−sin2(r)
- Substituting sin(r)=nsin(θ):
cos2(r)=1−(nsin(θ))2
- Thus:
cos(r)=√1−n2sin2(θ)
6. Substituting Back into the Diameter Equation:
- Now substituting cos(r) back into the diameter equation:
CD=b⋅√1−n2sin2(θ)
7. Final Expression:
- Therefore, the diameter of the beam when it goes to air through the face is:
CD=b√1−n2sin2(θ)
- We have a beam of parallel rays of diameter b propagating in glass with a refractive index n at an angle θ to the normal of the surface.
- The angle of incidence i is given as θ.
- According to Snell's law, the relationship between the angles and the refractive indices is given by:
nsin(i)=sin(r)
- Here, r is the angle of refraction when the beam exits into air (where the refractive index is approximately 1).
- From Snell's law, we can express:
nsin(θ)=sin(r)
- This implies:
sin(r)=nsin(θ)
- The diameter of the beam after refraction can be expressed in terms of the original diameter and the angles involved.
- For the triangle formed by the rays, we can use the cosine of the angle of refraction:
CD=AB⋅cos(r)
- Since AB=b, we have:
CD=b⋅cos(r)
- We can find cos(r) using the identity:
cos2(r)=1−sin2(r)
- Substituting sin(r)=nsin(θ):
cos2(r)=1−(nsin(θ))2
- Thus:
cos(r)=√1−n2sin2(θ)
- Now substituting cos(r) back into the diameter equation:
CD=b⋅√1−n2sin2(θ)
- Therefore, the diameter of the beam when it goes to air through the face is:
CD=b√1−n2sin2(θ)
Topper's Solved these Questions
Similar Questions
A beam of parallel rays of width b cm propagates in glass at an angle θ to its plane face. What would the beam width b1 be after it goes over to air thrugh this face? (The refractive index of the glass is μ)
View SolutionA narrow beam of white light goes through a slab having parallel faces.
View Solution
Knowledge Check
Consider a light beam incident from air to a glass slab at Brewster's angle as shown in figure.
A polaroid is placed in the path of the emergent ray at point P and rotated about an axis passing through the centre and pependicular to the plane of the plaroid.
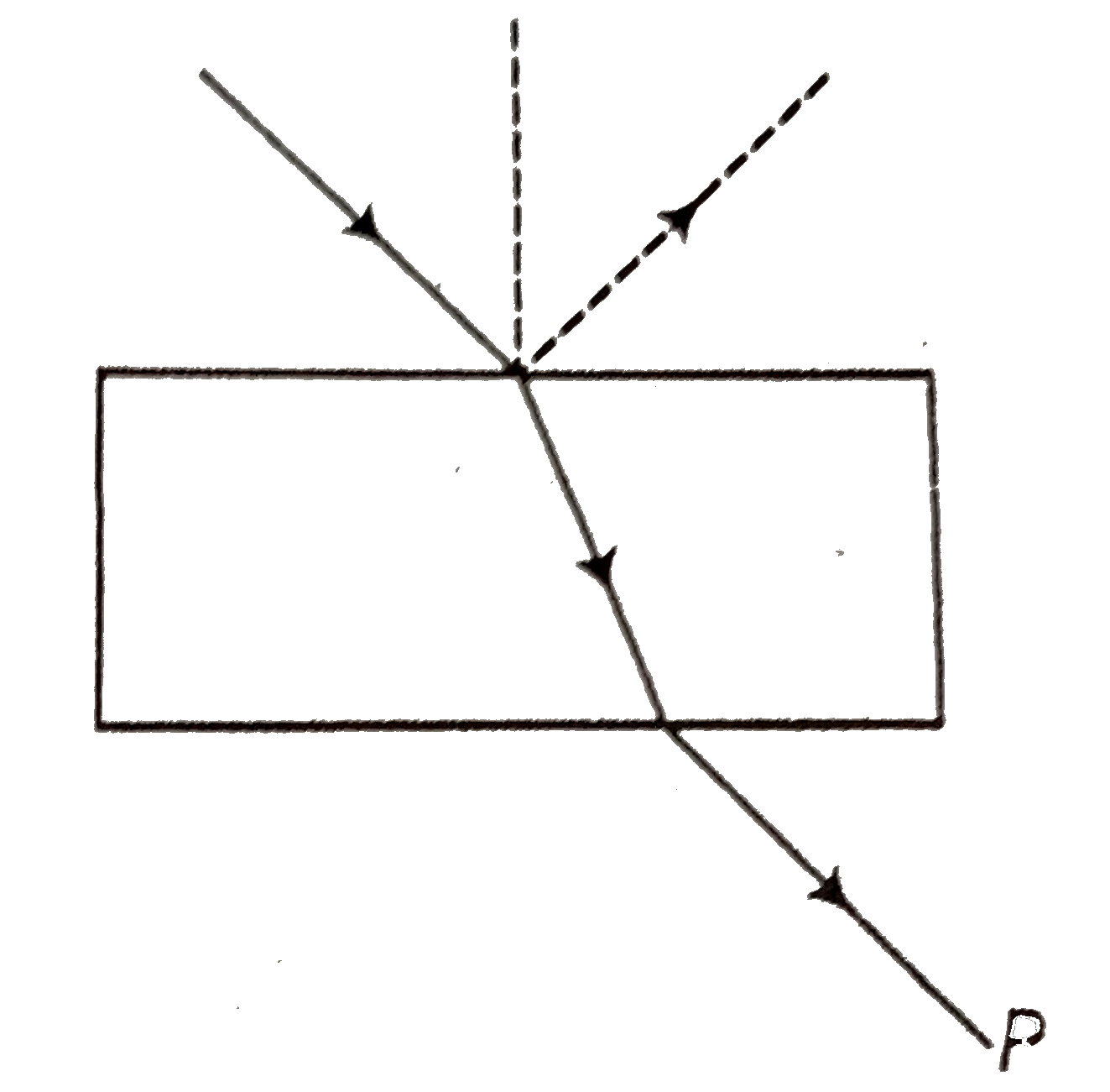 AFor a paricular orientation there shall be darkness as observed through the polaroid.BThe intensity of light as seen through the polaroid shall be independent of the rotation.CThe intensity of light as seen through the polaroid shall go through a minimum but not zero for two orientations of the polaroid.DThe intensity of light as seen through the polaroid shall go through a minimum for four orientations of the polaroid.
AFor a paricular orientation there shall be darkness as observed through the polaroid.BThe intensity of light as seen through the polaroid shall be independent of the rotation.CThe intensity of light as seen through the polaroid shall go through a minimum but not zero for two orientations of the polaroid.DThe intensity of light as seen through the polaroid shall go through a minimum for four orientations of the polaroid.
A beam of light falls on a glass plate (μ=3/2) of thickness 6.0 cm at an angle of 60∘. Find the deflection of the beam on passing through the plate. (in cm).
View SolutionA parallel beam of particles each of mass m moving with velocity v impinges on a wall at an angle θ to its normal. The number of particles per unit volume in the beam is n. If the collision of particles with the wall is elastic, then the pressure exerted by this beam on the wall is
View SolutionThere is layer of medium of variable refractive index μ=√2−1√2y (where 0≤t<1/2) sandwitched between the layer of glass and air A beam of light travelling in air at an angle 45∘ has a width Δω. When the beam enters the layer of glass its width becomes : (μglass=√2)
View SolutionConsider a light beam incident from air to a glass slab at Brewster's angle as shown in figure.
A polaroid is placed in the path of the emergent ray at point P and rotated about an axis passing through the centre and pependicular to the plane of the polaroid.

View SolutionConsider a light beam incident from air to a glass slab at Brewster's angle as shown in figure.
A polaroid is placed in the path of the emergent ray at point P and rotated about an axis passing through the centre and pependicular to the plane of the plaroid.

View SolutionA ray of light travelling in glass having refractive index _(a)μg=3/2 is incident at a critical angle C on the glass air interface. If a thin layer of water is poured on glass air interface, then what will be the angle of emergence of this ray in air when it emerges from water air inteface?
View SolutionWhen a plane mirror is rotated through an angle θ then the reflected ray turns through the angle 2θ then the size of the image
View Solution
