A thin equiconvex lens made of glass of refractive index and of focal length in air is sealed into an opening at one end of a tank filled with water . On the opposite side of the lens, a mirror is placed inside the tank on the tank wall perpendicular to the lens axis as shown in Figure. The separation between the lens and mirror is A small object is placed outside the tank in front of the lens at a distance oa from the lens along its axis. Find the position (relative to lens) of the image of the object formed by the system.

The correct Answer is: from the lens towards right
Form lens Maker's formula,
we have
Now applying at air galss surface, we get
first iamge will be formed at from the lens. This will act as the virtual object for glass water surface. Therefore, applying at glass water surface,
We have
second iamge is formed at from the lens or from the plane mirror. This will act as virtual object for mirror. Therefore, third real iamge will be formed at a distance of in front of the mirror after reflection form it. Now this iamge will work as a real object for water-glass interface. Hence, applying
fourth iamge is relative to the lens (rightward) or the image is formed behind the mirror .
Topper's Solved these Questions
- GEOMATRICAL OPTICS Book:RESONANCE ENGLISHChapter:GEOMATRICAL OPTICS Exercise:Exercise-3
Explore 80 Videos
- EXPERIMENTAL PHYSICSBook:RESONANCE ENGLISHChapter:EXPERIMENTAL PHYSICSExercise:PART -II
Explore 10 Videos
- GRAVITATIONBook:RESONANCE ENGLISHChapter:GRAVITATIONExercise:HIGH LEVEL PROBLEMS
Explore 16 Videos
Similar Questions
A plano-convex lens is made of refractive index of 1.6. The focal length of the lens is
View SolutionA thin lens made of glass of refractive index μ=1.5 has a focal length equal to 12 cm in air. It is now immersed in water (μ=43). Its new focal length is
View SolutionA thin equi-convex lens is made of glass of refractive index 1.5 and its length is 0.2m. If it acts as a concave lens of 0.5m focal length when dipped in a liquid, the refractive index of the liquid is
View SolutionA thin lens made of a material of refractive index μ0 has a focal length f0 in air. Find the focal length of this lens if it is immersed in a liquid of refractive index μ.
View SolutionA convex lens of focal length 15 cm and concave mirror of focal length 30 cm are kept their optical axes PQ and RS parallel but separated in vertical direction by 0.6 m, as shown. The distance between the lens and mirror is 30 cm. An upright object AB of height 1.2 m is placed on the optic axic PQ of the lens at a distance of 20 cm from the lens.

Find the linear magnification of the first image after refraction from the lens.
View SolutionAn equiconvex lens of glass (μg=1.5) of focal length 10 cm is silvered on one side. It will behave like a
View SolutionA convex lens of focal length 15 cm and concave mirror of focal length 30 cm are kept their optical axes PQ and RS parallel but separated in vertical direction by 0.6 m, as shown. The distance between the lens and mirror is 30 cm. An upright object AB of height 1.2 m is placed on the optic axic PQ of the lens at a distance of 20 cm from the lens.

Find the linear magnification of the second image after reflection from the mirror.
View SolutionA convex lens of focal length 15 cm and concave mirror of focal length 30 cm are kept their optical axes PQ and RS parallel but separated in vertical direction by 0.6 m, as shown. The distance between the lens and mirror is 30 cm. An upright object AB of height 1.2 m is placed on the optic axic PQ of the lens at a distance of 20 cm from the lens.

As in the lat problem, find the distance of A' below the optic axis of lens.
View SolutionA lens of refractive index n is put in a liquid of refractive index n'. If focal length of lens in air is f, its focal length in liquid will be.
View SolutionA concave mirror of focal length 20 cm and a convex lens of focal length 10 cm are kept with their optic axes parallel but separated by 0.5 mm as shown in the figure. The distance between the the lens and mirror in 10 cm. An object of height 3 mm is placedon the optic axis of lens at a distnace between the lens and mirror is 10 cm. An object of height 3 mm is placed on the optic axis of lens at a distance 15 cm from the lens. Find the length of the image formed the mirror in mm.
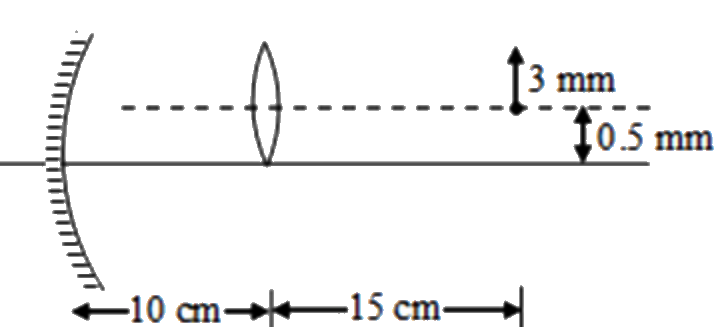
View Solution

