An object is kept at rest on the principal axis of a lens. Initially the object is at a distance three times the focal length 'f' of the lens. The lens runs towards the object at a constant speed u, until the distance between the object and its real image becomes 4f. If the iamge always forms on a moving screen then express the velocity of the screen as a function of time.
The correct Answer is:vi=u[1−{fut−2f}2]
To solve the problem step by step, let's break it down:
Step 1: Understand the Initial Setup
The object is placed at a distance of 3f from the lens, where f is the focal length of the lens. The lens moves towards the object at a constant speed u.
Step 2: Determine the Distance Between the Object and the Lens
As the lens moves towards the object, the distance between the lens and the object at time t can be expressed as:
d=3f−ut
Here, d is the distance from the lens to the object at time t.
Step 3: Use the Lens Formula
The lens formula is given by:
1f=1u+1v
Where:
- u is the object distance (which we have as d),
- v is the image distance.
Substituting d into the lens formula gives:
1f=13f−ut+1v
Step 4: Rearranging the Lens Formula
Rearranging the lens formula to find v:
1v=1f−13f−ut
Combining the fractions:
1v=(3f−ut)−ff(3f−ut)=2f−utf(3f−ut)
Thus, we can express v as:
v=f(3f−ut)2f−ut
Step 5: Differentiate to Find Velocity of the Image
To find the velocity of the image vi, we differentiate v with respect to time t:
dvdt=ddt(f(3f−ut)2f−ut)
Using the quotient rule:
dvdt=(2f−ut)(−fu)−f(3f−ut)(−u)(2f−ut)2
Simplifying this expression gives:
dvdt=−fu(2f−ut)+fu(3f−ut)(2f−ut)2
This simplifies to:
dvdt=fu(f)(2f−ut)2
Step 6: Express the Velocity of the Screen
Since the image is always formed on a moving screen, the velocity of the screen vs is equal to the velocity of the image:
vs=fu2(2f−ut)2
Final Result
Thus, the velocity of the screen as a function of time is:
vs=fu2(2f−ut)2
The object is placed at a distance of 3f from the lens, where f is the focal length of the lens. The lens moves towards the object at a constant speed u.
As the lens moves towards the object, the distance between the lens and the object at time t can be expressed as:
d=3f−ut
Here, d is the distance from the lens to the object at time t.
The lens formula is given by:
1f=1u+1v
Where:
- u is the object distance (which we have as d),
- v is the image distance.
1f=13f−ut+1v
Rearranging the lens formula to find v:
1v=1f−13f−ut
Combining the fractions:
1v=(3f−ut)−ff(3f−ut)=2f−utf(3f−ut)
Thus, we can express v as:
v=f(3f−ut)2f−ut
To find the velocity of the image vi, we differentiate v with respect to time t:
dvdt=ddt(f(3f−ut)2f−ut)
Using the quotient rule:
dvdt=(2f−ut)(−fu)−f(3f−ut)(−u)(2f−ut)2
Simplifying this expression gives:
dvdt=−fu(2f−ut)+fu(3f−ut)(2f−ut)2
This simplifies to:
dvdt=fu(f)(2f−ut)2
Since the image is always formed on a moving screen, the velocity of the screen vs is equal to the velocity of the image:
vs=fu2(2f−ut)2
Thus, the velocity of the screen as a function of time is:
vs=fu2(2f−ut)2
Topper's Solved these Questions
- GEOMATRICAL OPTICS Book:RESONANCE ENGLISHChapter:GEOMATRICAL OPTICS Exercise:Exercise-3
Explore 80 Videos
- EXPERIMENTAL PHYSICSBook:RESONANCE ENGLISHChapter:EXPERIMENTAL PHYSICSExercise:PART -II
Explore 10 Videos
- GRAVITATIONBook:RESONANCE ENGLISHChapter:GRAVITATIONExercise:HIGH LEVEL PROBLEMS
Explore 16 Videos
Similar Questions

The distance between a convex lens and a plane mirror is 10 cm. The parallel rays incident on the convex lens after reflection from the mirror forms image at the optical centre of the lens. Focal length of lens will be
View SolutionThe minimum distance between an object and its real image formed by a convex lens is
View SolutionThe minimum distance between a real object and its real image formed by a thin converging lens of focal length f is
View SolutionThe distance between the object and its real image from the convex lens is 60 cm and the height of image is two times the height of object . The focal length of the lens is
View SolutionThe graph shown relationship between object distance and image distance for a equiconvex lens. Then focal length of the lens is
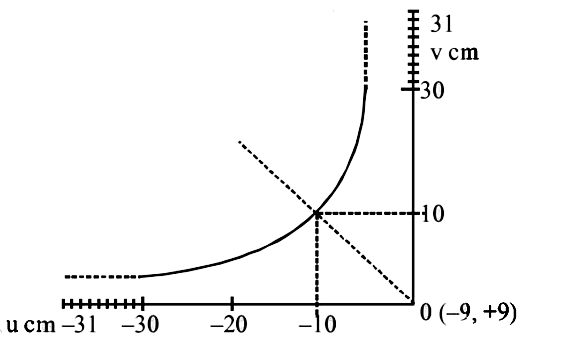
View SolutionThe distance between an object and a divergent lens is m times the focal length of the lens. The linear magnification produced by the lens is
View SolutionAn object is placed at a distance u from an equiconvex lens such that the distannce between the object and its real image is minimum. The focal length of the lens is f. The value of u is
View SolutionA lens of focal length 12cm forms an upright image three times the size of a real object. Find the distance in cm between the object and image.
View SolutionThe minimum distance between an object and its real image formed by a thin convex lens of focal length f is K.f. Find the value of K.
View SolutionA thin linear object of size 1mm is kept along the principal axis of a convex lens of focal length 10cm. The object is at 15cm from the lens. The length of the image is:
View Solution