Two thin convex lenses of focal lengths f1 and f2 are separated by a horizontal distance d (whered<f1,d<f2) and their centres are displaced by a vertical separation △ as shown in the fig.
Taking the origin of coordinates O, at the centre of the first lens the x and y coordinates of the focal point of this lens system, for a parallel beam of rays coming form the left, are given by:
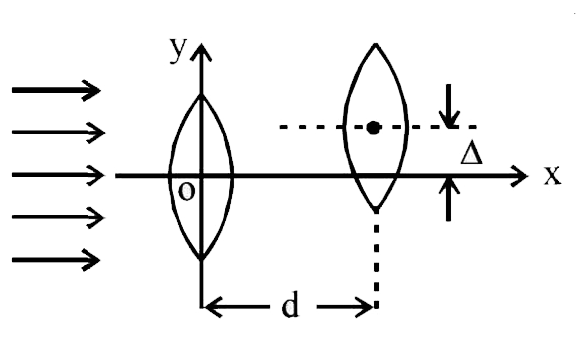
d(f1−d)+f1f2(f1+f2−d)
f1f2(f1+f2−d)
d(f1−d)(f1+f2−d)
2d(f1+d)−f1f2(f1+f2−d)
The correct Answer is:a
The parallel rays will be focussed at the focal point of the first lens. The first image lies at I, at a distance f1 from the origin. This imageI1 will act as an object for refraction through the second lens. The object distance for the second, u=(f1−d).
From lens equation, 1υ−1+(f1−d)=1f2
υ=f2(f1−d)(f1+f2−d)
Hence, the x-coordinate of final image I2 is
x=d+u=d+f2(f1−d)(f1+f2−d)=d(f1−d)+f1f2(f1+f2−d)
Imagine an arrow tip is at f1: its image from lens f1 is the final image.
Magnification, m+υu=I2O=I2Δ
I2=(υu)Δ=f2(f1+f2−d)Δ
Thus, y-coordinate of tip of I2 is
Δ−I2=Δ[1−f1(f1+f2−d)]=(f1−d)Δ(f1+f2−d)

Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Integer15videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Archives7videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Assertion-Reasoninig2videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.315videos
ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit27videos
HEATING EFFECT OF CURRENT
Similar Questions
Two thin lenses of focal lengths f1 and f2 are in contact. The focal length of this combination is
View SolutionTwo thin lenses of focal length f1 and f2 are in contact and coaxial. The power of the combination is
View SolutionTwo converging lenses of focal lengths f1=10cm and f2=20cm are placed at some separation. A parallel beam of light is incident on first lens. Then,
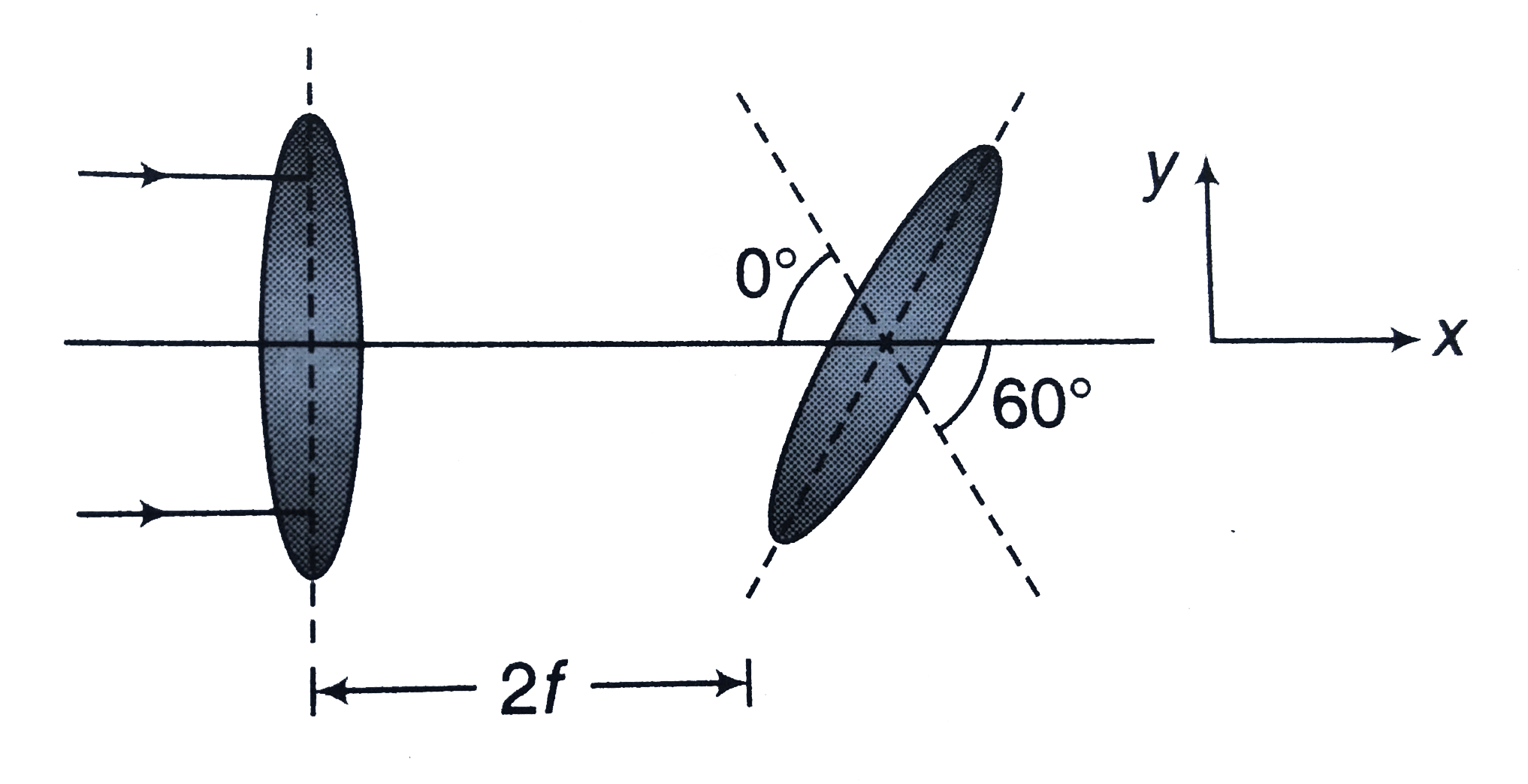
View SolutionTwo converging lenses of the same focal length f are separated by a distance 2f. The axis of the second lens is inclined at angle θ=60∘ with respect to the axis of the first lens. A parallel paraxial beam of light is incident from left side of the lens. Find the coordinates of the final image with respect to the origin of the first lens.
 View Solution
View SolutionA convex lens of focal length f1 is kept in contact with a concave lens of focal length f2. Find the focal length of the combination.
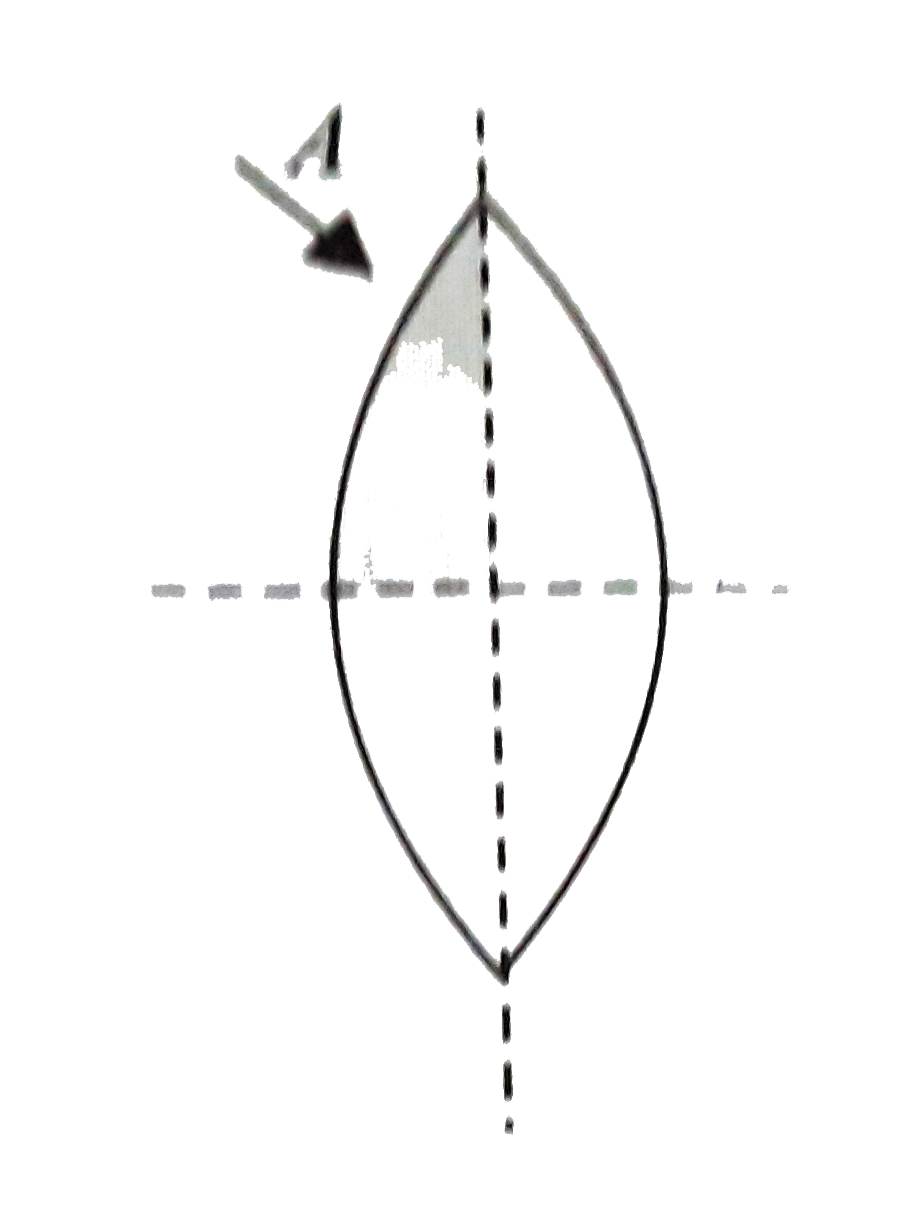
View SolutionA convex lens of focal length f cut into parts first horizontally and then vertically. Find the focal length of part A of the lens, as shown:
 View Solution
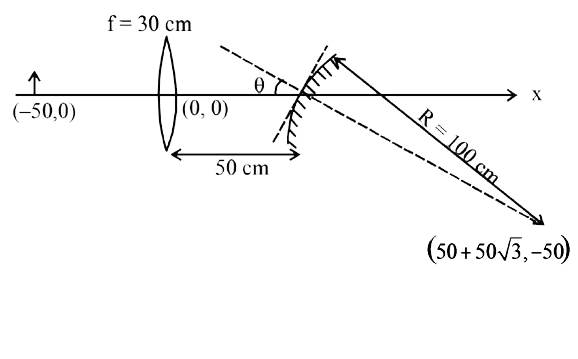
View SolutionA small object is placed 50 cm to the left of a thin convex lens of focal length 30 cm. A convex spherical mirror of radius of curvature 100 cm is placed to the right of the lens at a distance of 50 cm. The mirror is tilted such that the axis of the mirror is at an angle θ=30degree to the axis of the lens, as shown in the figure
If the origin of the coordinate system is taken to be at the centre of the lens, the coordinates (in cm) of the point (x,y) at which the image is formed are
 View Solution
View SolutionCalculate the focal length of the thin lens shown infigure. The pionts C1andC2 denote the centres of curvature.
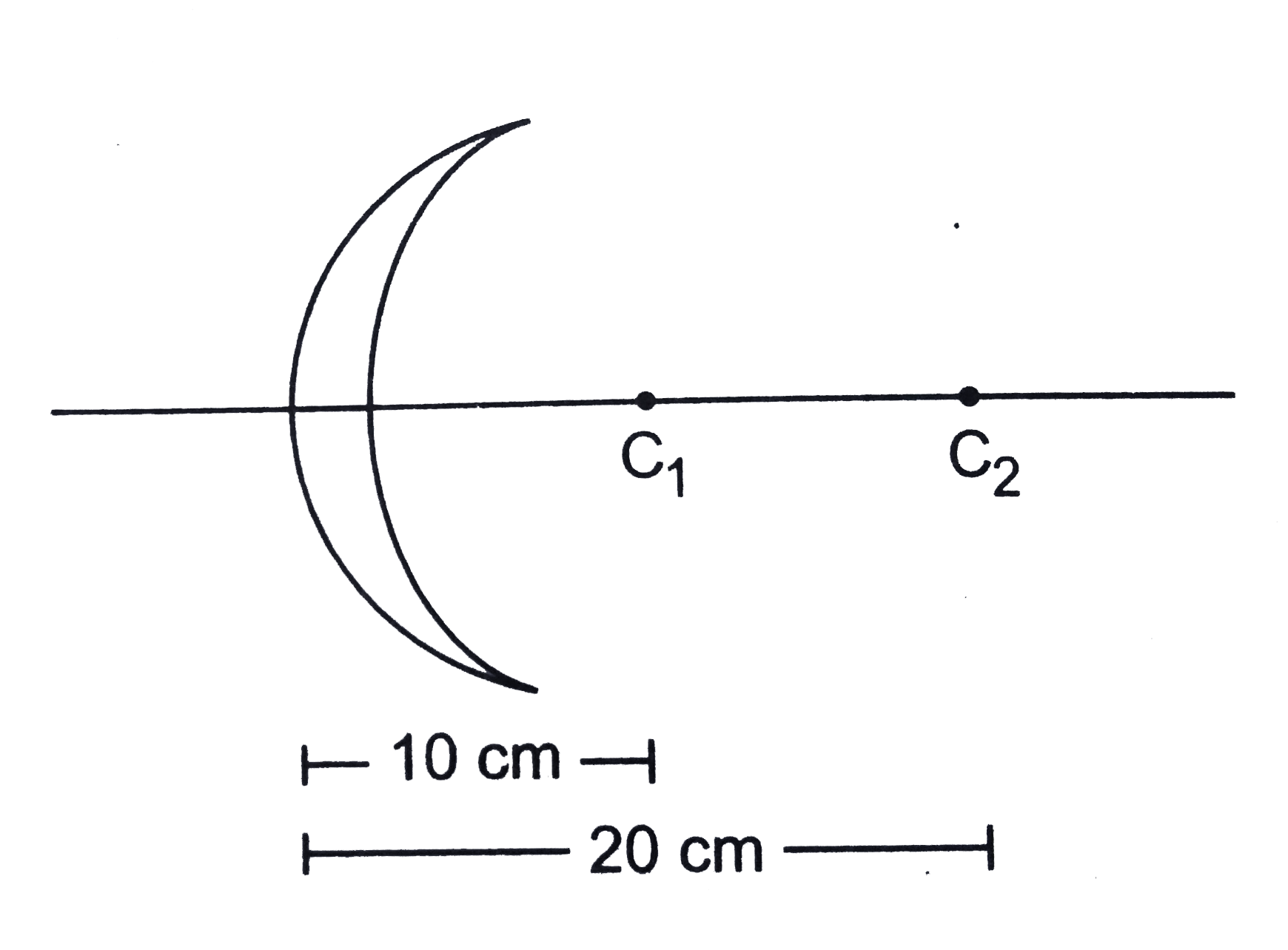 View Solution
View SolutionTwo lenses of power 6 D and – 2 D are combined to form a single lens. The focal length of this lens will be
View SolutionIn the figure shown, there are two convex lenses L1 and L2 having focal. Lengths f1 and f2 respectively. The distance between L1 and L2 will be
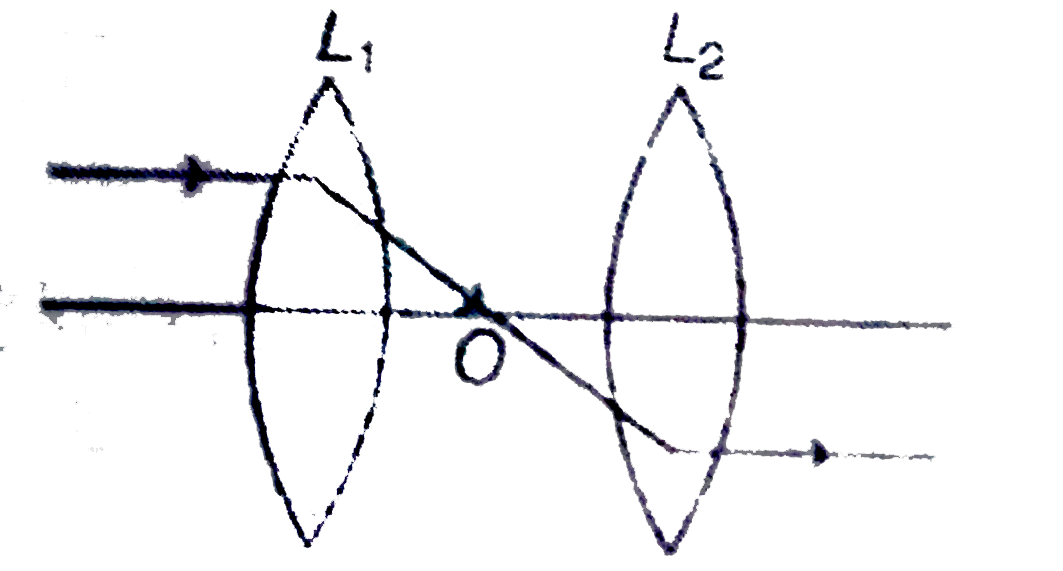 View Solution
View Solution
