Show that the factor (and therefore focal length) does not depend on which surface of the lens strike first.
To show that the factor (1R1−1R2) (and therefore the focal length) does not depend on which surface of the lens the light strikes first, we can analyze the situation using the lens maker's formula.
1. Understanding the Lens Maker's Formula:
The lens maker's formula is given by:
1f=μrelative(1R1−1R2)
where f is the focal length, μrelative is the relative refractive index of the lens material with respect to the surrounding medium, and R1 and R2 are the radii of curvature of the two surfaces of the lens.
2. Case 1: Light Striking Surface 1 First:
- Assume light is coming from the left and strikes the first surface (with radius of curvature R1).
- Since the light travels in the positive direction, we take R1 as positive (if it is convex) and R2 as negative (if it is concave).
- The lens maker's formula becomes:
1f=μrelative(1R1−1R2)
3. Case 2: Light Striking Surface 2 First:
- Now consider light coming from the right and striking the second surface (with radius of curvature R2) first.
- In this case, R2 is positive (if it is convex) and R1 is negative (if it is concave).
- The lens maker's formula becomes:
1f=μrelative(1R2−1R1)
4. Rearranging the Second Case:
- We can rearrange the second case:
1f=μrelative(−1R1+1R2)=μrelative(1R2−1R1)
- Notice that this is equivalent to:
1f=μrelative(1R1−1R2)
after factoring out the negative sign.
5. Conclusion:
- In both cases, the expression (1R1−1R2) remains the same, demonstrating that the focal length f does not depend on which surface the light strikes first.
The lens maker's formula is given by:
1f=μrelative(1R1−1R2)
where f is the focal length, μrelative is the relative refractive index of the lens material with respect to the surrounding medium, and R1 and R2 are the radii of curvature of the two surfaces of the lens.
- Assume light is coming from the left and strikes the first surface (with radius of curvature R1).
- Since the light travels in the positive direction, we take R1 as positive (if it is convex) and R2 as negative (if it is concave).
- The lens maker's formula becomes:
1f=μrelative(1R1−1R2)
- Now consider light coming from the right and striking the second surface (with radius of curvature R2) first.
- In this case, R2 is positive (if it is convex) and R1 is negative (if it is concave).
- The lens maker's formula becomes:
1f=μrelative(1R2−1R1)
- We can rearrange the second case:
1f=μrelative(−1R1+1R2)=μrelative(1R2−1R1)
- Notice that this is equivalent to:
1f=μrelative(1R1−1R2)
after factoring out the negative sign.
- In both cases, the expression (1R1−1R2) remains the same, demonstrating that the focal length f does not depend on which surface the light strikes first.
Topper's Solved these Questions
- GEOMATRICAL OPTICS Book:RESONANCE ENGLISHChapter:GEOMATRICAL OPTICS Exercise:Problem
Explore 33 Videos
- GEOMATRICAL OPTICS Book:RESONANCE ENGLISHChapter:GEOMATRICAL OPTICS Exercise:Exercise-1
Explore 141 Videos
- EXPERIMENTAL PHYSICSBook:RESONANCE ENGLISHChapter:EXPERIMENTAL PHYSICSExercise:PART -II
Explore 10 Videos
- GRAVITATIONBook:RESONANCE ENGLISHChapter:GRAVITATIONExercise:HIGH LEVEL PROBLEMS
Explore 16 Videos
Similar Questions
Show that r1+r2=ccot(C2)
View SolutionStatement-1 : A glass convex lens (refractive index, μ1=1.5), when immersed in a liquid of refractive index μ2=2, functions as a diverging lens.
Statement-2 : The focal length of a lens is given by 1f=(μ−1)(1R1−1R2), where μ is the relative refractive index of the material of the lens with respect to the surrounding medium.
View Solution(a) Using the ray diagram for a system of two lenses of focal lengths f1andf2 in contact with each other, show that the two lens system can be regarded as equivalent to a single lens of focal length f, where
1f=1f1+1f2
Also write the relation for the equivalent power of the lens combination.
(b) Determine the position of the image formed by the lens combination given in the figure.
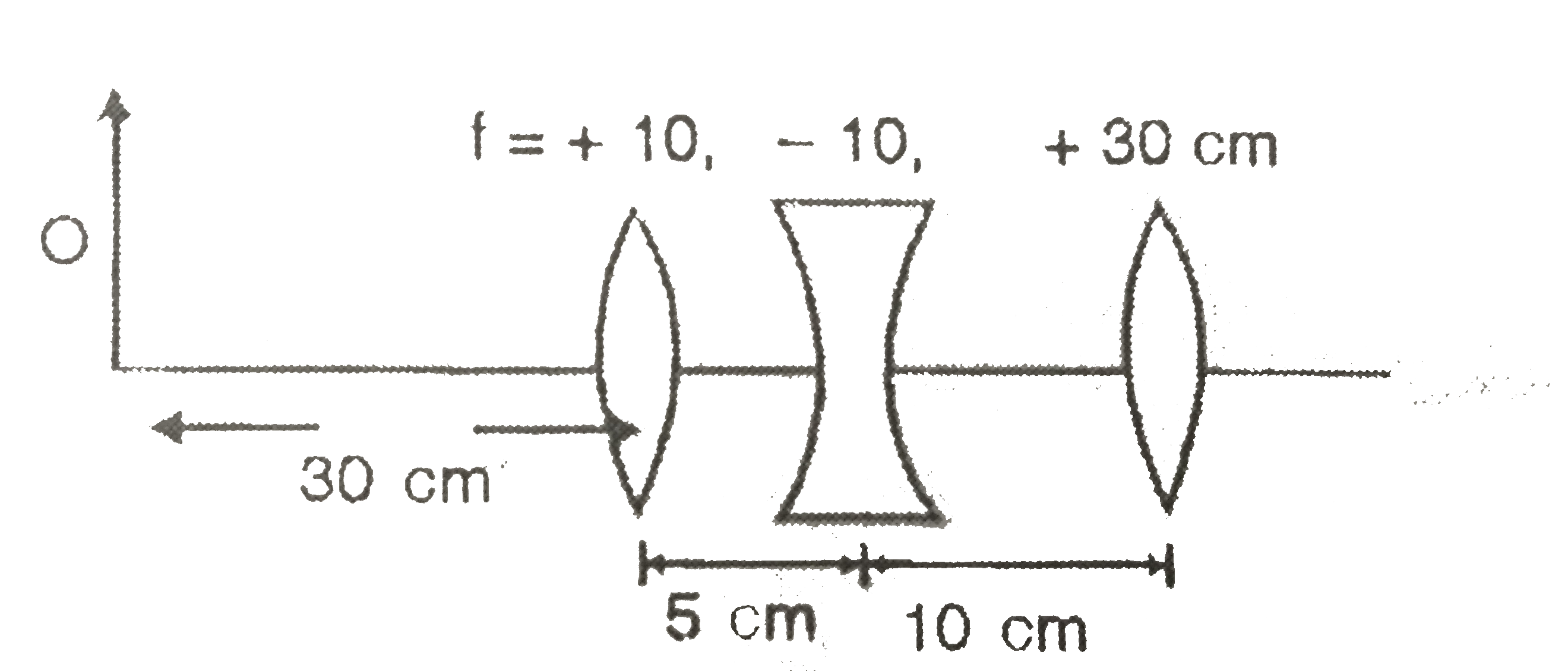
View SolutionFind the focal length of the lens shown in Fig . The radii of curvature of both the surfaces are equal to R.
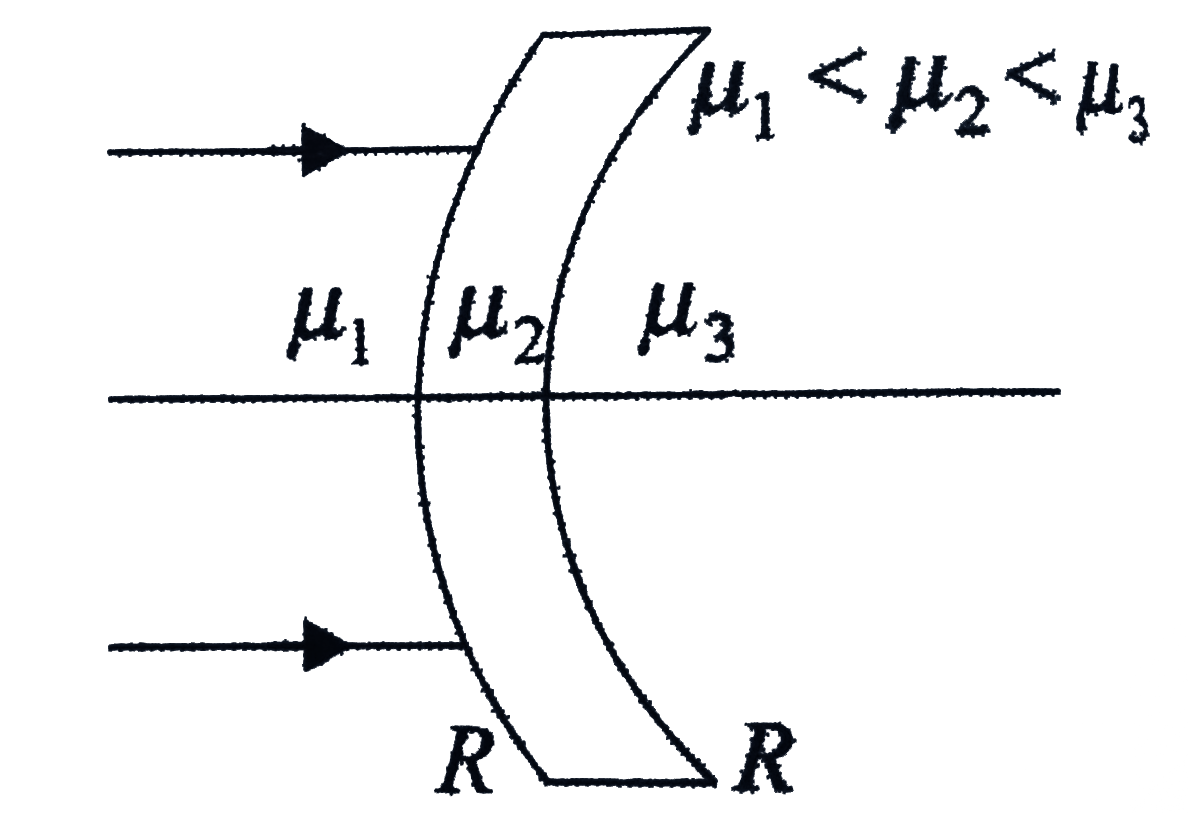
View SolutionRadius of curvature of first surface of double convex lens is three times that of the other. If focal length of the lens is 30 cm and refractive index of the lens is 3/2, then radius of curvature of the first surface is
View SolutionIf R1andR2 are the radii of curvature of the spherical surfaces of a thin lens and R1>R2, then this lens can
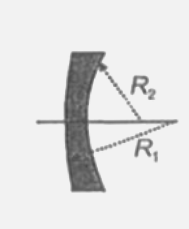
View SolutionWhich one of the following sperical lenses does not exhibit dispersion? The radii of curvature of the surfaces of the lenses are as given in the diagrams.
R1≠R2
View SolutionA plano-convex lens fits exactly into a plano-concave lens. Their plane surfaces are parallel to each other. If the lenses are made of different material of refractive indices μ1 and μ2 and R is the radius of curvature of the curved surface of the lenses, then focal length of the combination is
View SolutionThe power of lens is P=1f' where f is focal length of the lens. The dimensions of power of lens is
View SolutionThe power of lens is P=1f where f is focal length of the lens. The dimensions of power of lens is
View Solution