A solid sphere of radius is floating in a liquid of density with half of its volume submerged. If the sphere is slightly pushed and released , it starts axecuting simple harmonic motion. Find the frequency of these oscillations.
The correct Answer is:8
To find the frequency of oscillations of a solid sphere floating in a liquid, we can follow these steps:
Step 1: Understand the equilibrium condition
When the sphere is floating, the buoyant force acting on it is equal to its weight. The buoyant force Fb can be expressed as:
Fb=σ⋅Vs⋅g
where σ is the density of the liquid, Vs is the volume of the submerged part of the sphere, and g is the acceleration due to gravity.
Step 2: Determine the volume submerged
Given that half of the sphere is submerged, the volume submerged Vs is:
Vs=12⋅V
where V is the total volume of the sphere. The volume of a sphere is given by:
V=43πR3
Thus, the submerged volume becomes:
Vs=12⋅43πR3=23πR3
Step 3: Calculate the weight of the sphere
The weight W of the sphere can be expressed as:
W=ρs⋅V⋅g
where ρs is the density of the sphere. Substituting the volume of the sphere:
W=ρs⋅43πR3⋅g
Step 4: Set up the equilibrium condition
At equilibrium, the buoyant force equals the weight of the sphere:
σ⋅23πR3⋅g=ρs⋅43πR3⋅g
Cancelling common terms, we find:
σ⋅23=ρs⋅43
From this, we can derive the density of the sphere:
ρs=σ2
Step 5: Analyze the displacement and the restoring force
When the sphere is displaced downward by a small distance x, the increase in submerged volume ΔV is:
ΔV=A⋅x
where A is the cross-sectional area of the sphere at the water surface, which is given by:
A=πR2
Thus, the increase in submerged volume becomes:
ΔV=πR2⋅x
Step 6: Calculate the increase in buoyant force
The increase in buoyant force ΔFb due to the additional submerged volume is:
ΔFb=σ⋅ΔV⋅g=σ⋅πR2⋅x⋅g
Step 7: Relate the restoring force to the mass of the sphere
The restoring force acting on the sphere when displaced is:
F=−ΔFb=−σ⋅πR2⋅g⋅x
This is analogous to Hooke's law, where F=−kx and k is the effective spring constant:
k=σ⋅πR2⋅g
Step 8: Find the mass of the sphere
The mass m of the sphere is:
m=ρs⋅V=σ2⋅43πR3=23πR3σ
Step 9: Calculate the frequency of oscillation
The frequency f of the oscillation is given by:
f=12π√km
Substituting the values of k and m:
f=12π
⎷σ⋅πR2⋅g23πR3σ=12π√3g2R
Final Result
Thus, the frequency of the oscillations is:
f=12π√3g2R
When the sphere is floating, the buoyant force acting on it is equal to its weight. The buoyant force Fb can be expressed as:
Fb=σ⋅Vs⋅g
where σ is the density of the liquid, Vs is the volume of the submerged part of the sphere, and g is the acceleration due to gravity.
Given that half of the sphere is submerged, the volume submerged Vs is:
Vs=12⋅V
where V is the total volume of the sphere. The volume of a sphere is given by:
V=43πR3
Thus, the submerged volume becomes:
Vs=12⋅43πR3=23πR3
The weight W of the sphere can be expressed as:
W=ρs⋅V⋅g
where ρs is the density of the sphere. Substituting the volume of the sphere:
W=ρs⋅43πR3⋅g
At equilibrium, the buoyant force equals the weight of the sphere:
σ⋅23πR3⋅g=ρs⋅43πR3⋅g
Cancelling common terms, we find:
σ⋅23=ρs⋅43
From this, we can derive the density of the sphere:
ρs=σ2
When the sphere is displaced downward by a small distance x, the increase in submerged volume ΔV is:
ΔV=A⋅x
where A is the cross-sectional area of the sphere at the water surface, which is given by:
A=πR2
Thus, the increase in submerged volume becomes:
ΔV=πR2⋅x
The increase in buoyant force ΔFb due to the additional submerged volume is:
ΔFb=σ⋅ΔV⋅g=σ⋅πR2⋅x⋅g
The restoring force acting on the sphere when displaced is:
F=−ΔFb=−σ⋅πR2⋅g⋅x
This is analogous to Hooke's law, where F=−kx and k is the effective spring constant:
k=σ⋅πR2⋅g
The mass m of the sphere is:
m=ρs⋅V=σ2⋅43πR3=23πR3σ
The frequency f of the oscillation is given by:
f=12π√km
Substituting the values of k and m:
f=12π
⎷σ⋅πR2⋅g23πR3σ=12π√3g2R
Thus, the frequency of the oscillations is:
f=12π√3g2R
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Exercise- 2, PART - II
Explore 1 Video
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Exercise- 2, PART - III
Explore 12 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Exercise- 1, PART - II
Explore 36 Videos
- SEMICONDUCTORSBook:RESONANCE ENGLISHChapter:SEMICONDUCTORSExercise:Exercise 3
Explore 88 Videos
- TEST PAPERSBook:RESONANCE ENGLISHChapter:TEST PAPERSExercise:PHYSICS
Explore 784 Videos
Similar Questions
A wooden cube (density of wood 'd') of side 'l' flotes in a liquid of density 'ρ' with its upper and lower surfaces horizonta. If the cube is pushed slightly down and released, it performs simple harmonic motion of period 'T'. Then, 'T' is equal to :-
View SolutionA cylindrical plastic bottle of negligible mass is filled with 310 ml of water and left floating in a pond with still water. If pressed downward slightly and released, it starts performing simple harmonic montion angular frequency ω. If the radius of the bottle is 2.5 cm then ω is close to: (density of water =103kg/m3)
View SolutionA cubical wood piece of mass 13.5 gm and volume 0.0027m3 float in water. It is depressed and released, then it executes simple harmonic motion. Calculate the period of oscillation ?
View SolutionA solid cube of side a and density ρ0 floats on the surface of a liquid of density ρ. If the cube is slightly pushed downward, then it oscillates simple harmonically with a period of
View SolutionA cylindrical object of outer diameter 20 cm and mass 2 kg floats in water with its axis vertical. If it is slightly depressed and then released, find the time period of the resulting simple harmonic motion of the object.
View SolutionFigure shown a container having liquid of variable density. The density of liquid veriesas ρ=ρ0(4−3hh0). Here, h0 and ρ0 are constants and h is measured from bottom of the container. A solid block of small dimensions whose density is 52ρ0 and mass m is released from bottom of the tank. Prove that the block will execute simple harmonic motion. Find the frequency of oscillation.
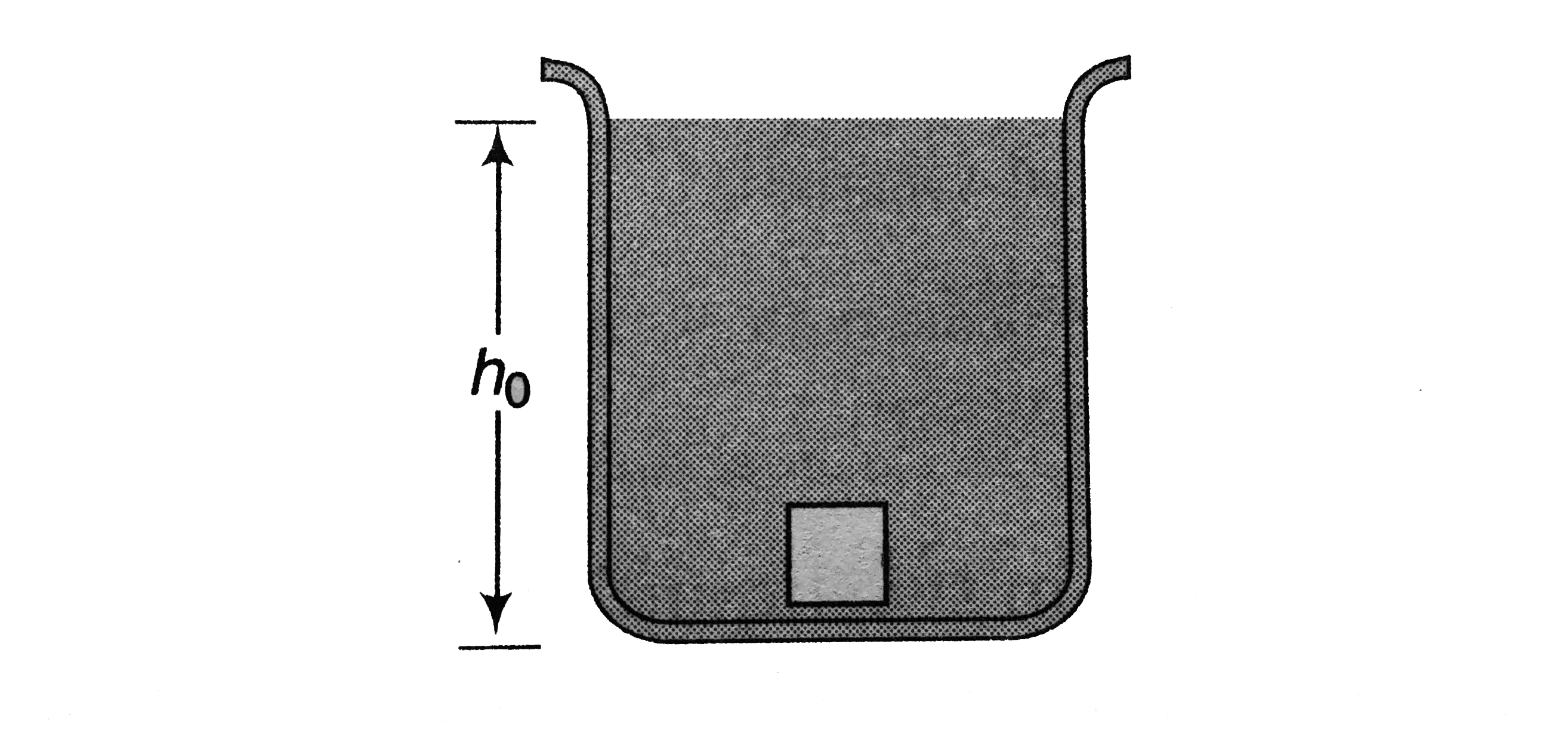 .
.
View SolutionA solid cube floats in a liquid of density ρ with half of its volume submerged as shown. The side length of the cube is a, which is very small compared to the size of the container. Now a liquid of density ρ3 (immiscible with the liquid already in the container) is poured slowly into the container. The column of the liquid of density ρ3 that must be poured so that the cube is fully submerged (with its top surface coincident with the surface of the poured liquid) is :

View SolutionA cylindrical block of wood of mass M is floating n water with its axis vertica. It is depressed a little and then released. Show that the motion of the block is simple harmonic and find its frequency.
View SolutionA solid sphere of radius r is floating at the interface of two immiscible liquids of densities ρ1 and ρ2(ρ2>ρ1), half of its volume lying in each. The height of the upper liquid column from the interface of the two liquids is h. The force exerted on the sphere by the upper liquid is (atmospheric pressure =p0 and acceleration due to gravity is g):
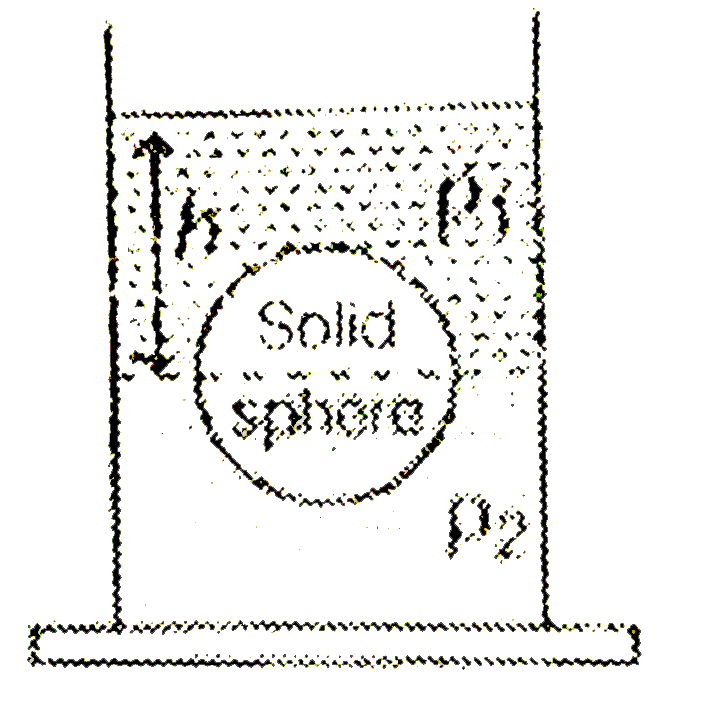
View SolutionA U-tube contains a liquid to a height of 9.8 cm in one of the limbs. The tube is vertical. If the liquid on one side is depressed a little and released its motion in the tube is simple harmonic motion. Find its period.
View Solution

