The period of small oscillations of a simple pendulum of length l if its point of suspension O moves a with a constant acceleration α=α1∧i−α2∧j with respect to earth is (∧i and ∧j are unit vectors in horizontal in horizontal and vertically upward directions respectively)
T=2π ⎷l{(g−α2)2+α21}1/2
T=2π ⎷l{(g−α1)2+α22}1/2
T=2π√lg
T=2π ⎷l(g2+α21)1/2
The correct Answer is:A
To find the period of small oscillations of a simple pendulum whose point of suspension is moving with constant acceleration, we can follow these steps:
1. Identify the Forces Acting on the Pendulum:
The pendulum is affected by gravitational force acting downward (denoted as g) and the acceleration of the point of suspension O which is moving with acceleration α=α1^i−α2^j.
2. Determine the Effective Acceleration:
The effective acceleration acting on the pendulum bob can be determined by considering both the gravitational acceleration and the acceleration of the point of suspension. The net acceleration →geffective can be expressed as:
→geffective=−α1^i+(g−α2)^j
Here, −α1^i represents the horizontal component and (g−α2)^j represents the vertical component.
3. Calculate the Magnitude of the Effective Acceleration:
The magnitude of the effective acceleration geffective is given by:
geffective=√(−α1)2+(g−α2)2
Simplifying this gives:
geffective=√α21+(g−α2)2
4. Use the Formula for the Period of a Pendulum:
The period T of a simple pendulum is given by the formula:
T=2π√Lgeffective
Substituting our expression for geffective into this formula, we have:
T=2π
⎷L√α21+(g−α2)2
5. Final Expression for the Period:
To simplify, we can express the period as:
T=2π
⎷L√α21+(g−α2)2
Conclusion
The period of small oscillations of the pendulum is given by:
T=2π
⎷L√α21+(g−α2)2
The pendulum is affected by gravitational force acting downward (denoted as g) and the acceleration of the point of suspension O which is moving with acceleration α=α1^i−α2^j.
The effective acceleration acting on the pendulum bob can be determined by considering both the gravitational acceleration and the acceleration of the point of suspension. The net acceleration →geffective can be expressed as:
→geffective=−α1^i+(g−α2)^j
Here, −α1^i represents the horizontal component and (g−α2)^j represents the vertical component.
The magnitude of the effective acceleration geffective is given by:
geffective=√(−α1)2+(g−α2)2
Simplifying this gives:
geffective=√α21+(g−α2)2
The period T of a simple pendulum is given by the formula:
T=2π√Lgeffective
Substituting our expression for geffective into this formula, we have:
T=2π
⎷L√α21+(g−α2)2
To simplify, we can express the period as:
T=2π
⎷L√α21+(g−α2)2
The period of small oscillations of the pendulum is given by:
T=2π
⎷L√α21+(g−α2)2
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Exercise- 2, PART - II
Explore 1 Video
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Exercise- 2, PART - III
Explore 12 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Exercise- 1, PART - II
Explore 36 Videos
- SEMICONDUCTORSBook:RESONANCE ENGLISHChapter:SEMICONDUCTORSExercise:Exercise 3
Explore 88 Videos
- TEST PAPERSBook:RESONANCE ENGLISHChapter:TEST PAPERSExercise:PHYSICS
Explore 784 Videos
Similar Questions
Find the period of oscillation of a pendulum of length l if its point of suspension is
(a) moving vertically up with acceleration a
(b) moving vertically down with acceleration a(<g)
(c) failing freely under gravity
moving horizontal with acceleration a.
View SolutionAn aeroplane is flying in vertical plane at an angle of 30∘ with the horizontal (north) and wind is is blowing from west.A package is dropped from an aeroplane. The velocity of the wind if package hits a kite flying in the space with a position vector →R=(400√3ˆi+80ˆj+200ˆk)m with respect to the point of dropping. (Here ˆi and ˆj are the unit vectors along north and vertically up respectively and ˆk be the unit vector due east. Assume that the bag is light enough to get carried away by the wind)
View SolutionA simple pendulum is suspended from the roof of a trolley which moves in a horizontal direction with an acceleration α, then the time period is given by T=2π√(Ig) where g is equal to
View SolutionA projectile is given an initial velocity of (ˆi+2ˆj) The Cartesian equation of its path is (g=10ms−1) ( Here , ˆi is the unit vector along horizontal and ˆj is unit vector vertically upwards)
View SolutionA simple pendulum of length l is suspended from the ceilling of a car moving with a speed v on a circular horizontal road of radius r. a. Find the tension in the string when it is at rest with respect to the car. b.Find the time period of small oscillation.
View SolutionA projectile is thrown with a velocity →v0=3ˆi+4ˆjms−1 where ˆIandˆj are the unit vectors along the horizontal and vertical directions respectively. The speed of the projectile at the highest point of its motion in ms−1 is
View SolutionA block of mass m is lying on a wedge having inclination angle α=tan−1(15) wedge is moving with a constant acceleration a=2ms−2 The minimum value of coefficient of friction μ so that m remain stationary w.r.t. wedge is

View SolutionA simple pendulum is suspended from the ceiling of a car and its period of oscillation is T when the car is at rest. The car starts moving on a horizontal road with a constant acceleration g (equal to the acceleration due to gravity, in magnitude) in the forward direction. To keep the time period same, the length of th pendulum
View Solution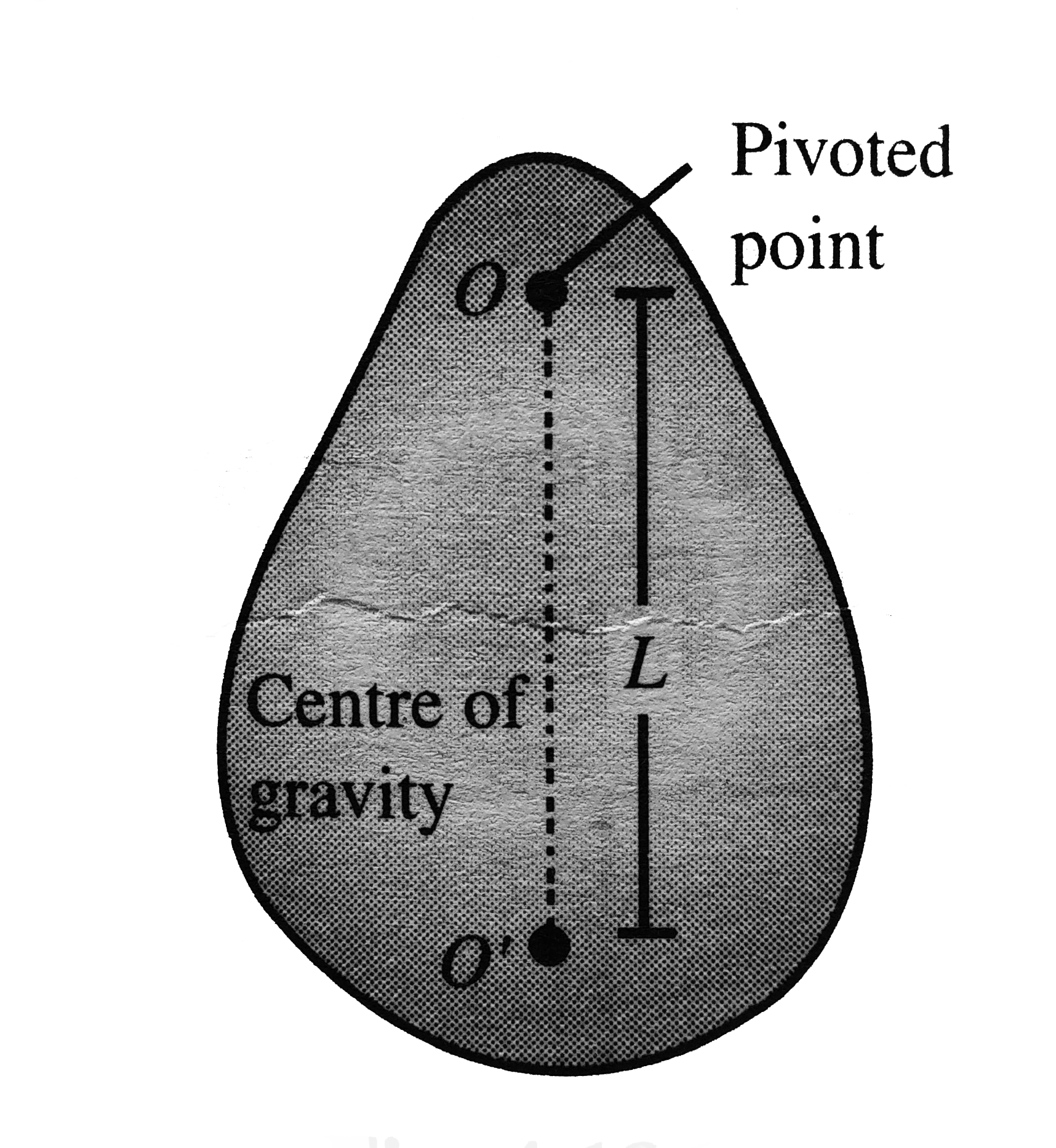
In physical pendulum, the time period for small oscillation is given by T=2π√IMgd where I is the moment of inertial of the body about an axis passing through a pivoted point O and perpendicular to the plane of oscillation and d is the separation point between centre of gravity and the pivoted point. In the physical pendulum a speacial point exists where if we concentrate the entire mass of body, the resulting simple pendulum (w.r.t. pivot point O) will have the same time period as that of physical pendulum This point is termed centre of oscillation.
T=2π√IMgd=2π√Lg Moreover, this point possesses two other important remarkable properties:
Property I: Time period of physical pendulum about the centre of oscillation (if it would be pivoted) is same as in the original case.
Property II: If an impulse is applied at the centre of oscillatioin in the plane of oscillation, the effect of this impulse at pivoted point is zero. Because of this property, this point is also known as the centre of percussion. From the given information answer the following question:
Q. A uniform rod of mass M and length L is pivoted about point O as shown in Figgt It is slightly rotated from its mean position so that it performs angular simple harmonic motion. For this physical pendulum, determine the time period oscillation.
View SolutionIn physical pendulum, the time period for small oscillation is given by T=2π√IMgd where I is the moment of inertial of the body about an axis passing through a pivoted point O and perpendicular to the plane of oscillation and d is the separation point between centre of gravity and the pivoted point. In the physical pendulum a speacial point exists where if we concentrate the entire mass of body, the resulting simple pendulum (w.r.t. pivot point O) will have the same time period as that of physical pendulum This point is termed centre of oscillation.
T=2π√IMgd=2π√Lg Moreover, this point possesses two other important remarkable properties:
Property I: Time period of physical pendulum about the centre of oscillation (if it would be pivoted) is same as in the original case.
Property II: If an impulse is applied at the centre of oscillatioin in the plane of oscillation, the effect of this impulse at pivoted point is zero. Because of this property, this point is also known as the centre of percussion. From the given information answer the following question:
Q. If an impulse J is applied at the centre of oscillation in the plane of oscillation, then angular velocity of the rod will be .

View Solution

