According to a scientists, he applied a force F=−cx1/3 on a particle and the particle is performing SHM. No other force acted on the particle. He refuses to tell whether c is a constant or not. Assume that he had worked only with positive x then :
as x increases c also increases
as x increases c also decreases
as x increases c remain constant
the motion cannot be SHM
The correct Answer is:A
To solve the problem, we need to analyze the force applied on the particle and its relation to Simple Harmonic Motion (SHM).
1. Identify the Force: The force applied on the particle is given by F=−cx1/3.
2. Condition for SHM: For a particle to be in SHM, the restoring force must be proportional to the displacement x and can be expressed as:
F=−mω2x
where m is the mass of the particle and ω is the angular frequency.
3. Equate the Forces: Since both expressions represent the force acting on the particle, we can set them equal to each other:
−cx1/3=−mω2x
By removing the negative signs, we have:
cx1/3=mω2x
4. Rearranging the Equation: We can rearrange this equation to express c:
c=mω2x1−1/3=mω2x2/3
5. Analyzing the Relationship: From the equation c=mω2x2/3, we can see that c is directly proportional to x2/3. This means that as x increases, c also increases.
6. Conclusion: Therefore, when x increases, c must also increase. This leads us to conclude that the correct answer to the question is that when x increases, c increases.
Final Answer:
When x increases, c also increases.
---
F=−mω2x
where m is the mass of the particle and ω is the angular frequency.
−cx1/3=−mω2x
By removing the negative signs, we have:
cx1/3=mω2x
c=mω2x1−1/3=mω2x2/3
When x increases, c also increases.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Exercise- 2, PART - I
Explore 26 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Exercise- 2, PART - II
Explore 1 Video
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Exercise- 1, PART - I
Explore 25 Videos
- SEMICONDUCTORSBook:RESONANCE ENGLISHChapter:SEMICONDUCTORSExercise:Exercise 3
Explore 88 Videos
- TEST PAPERSBook:RESONANCE ENGLISHChapter:TEST PAPERSExercise:PHYSICS
Explore 784 Videos
Similar Questions
A student says that he had applied a force F=−k√x on a particle and the particle performs in simple harmonic motion. He refuses to tell whether k is a constant or not. Assume that he has worked only with positive x and no other force acted on the particle.
View SolutionA student says that he had applied a force F=−k√x on a particle and the particle moved in simple harmonic motion. He refuses to tell whether k is a constant or not. Assume that he has worked only with positive x and no other force acted on the particle
View SolutionA time dependent force F=6t acts on a particle of mass 1kg. If the particle starts from rest, the work done by the force during the first 1sec. will be
View SolutionA position dependent force F ia acting on a particle and its force-position curve is shown in the figure. Work done on the particle, when its displacement is from 0 to 5 m is
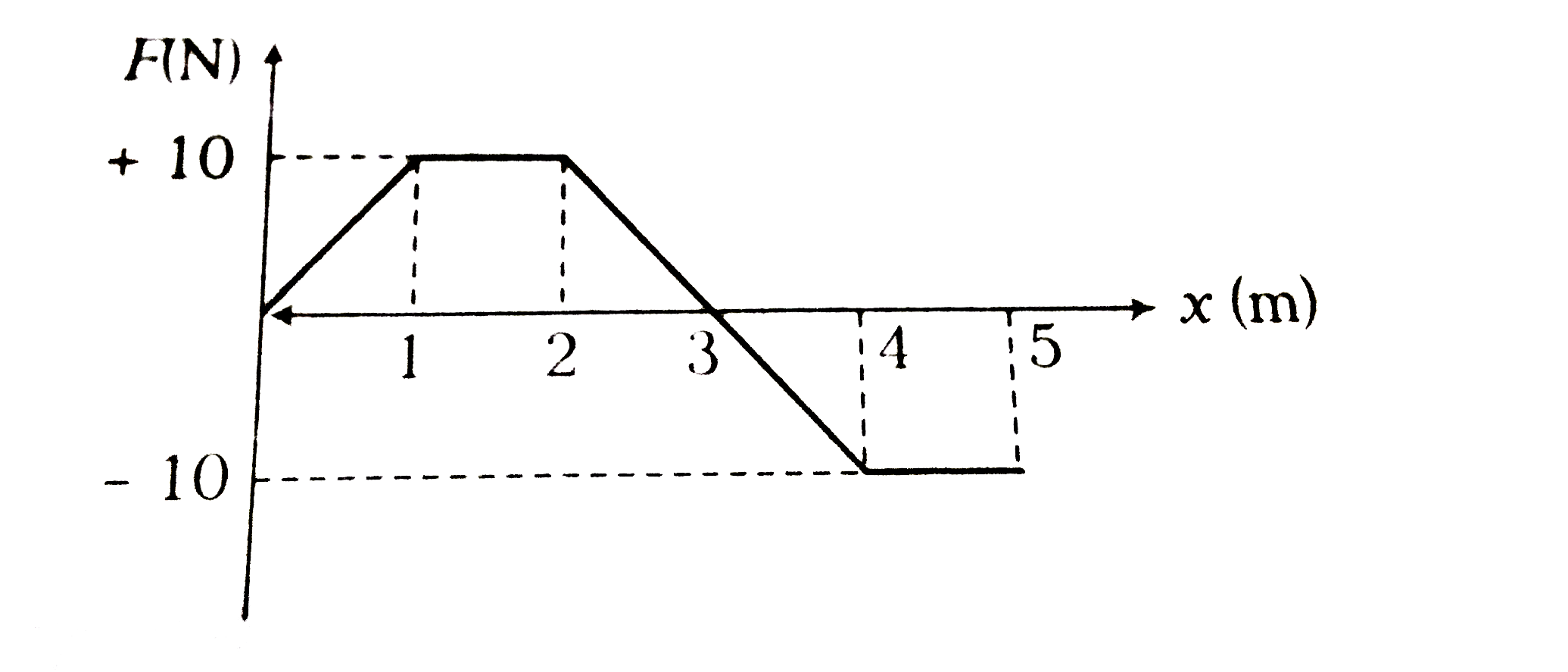
View SolutionUnder the action of a force F=−kx3 , the motion of a particle is (k=a positive constant)
View SolutionA force F=−kx2(x≠0) acts on a particle in x-direction. Find the work done by this force in displacing the particle from. x=+a to x=+2a. Where, k is a positive constant.
View SolutionA force F=−kx2(x≠0) acts on a particle in x-direction. Find the work done by this force in displacing the particle from. x=+a to x=2a. Here, k is a positive constant.
View SolutionThe power supplied by a force acting on a particle moving in a straight line is constant. The velocity of the particle varies with displacement as x1K. Find the value of K.
View SolutionA force F acting on a particle varies with the position x as shown in figure. Find the work done by this force in displacing the particle from
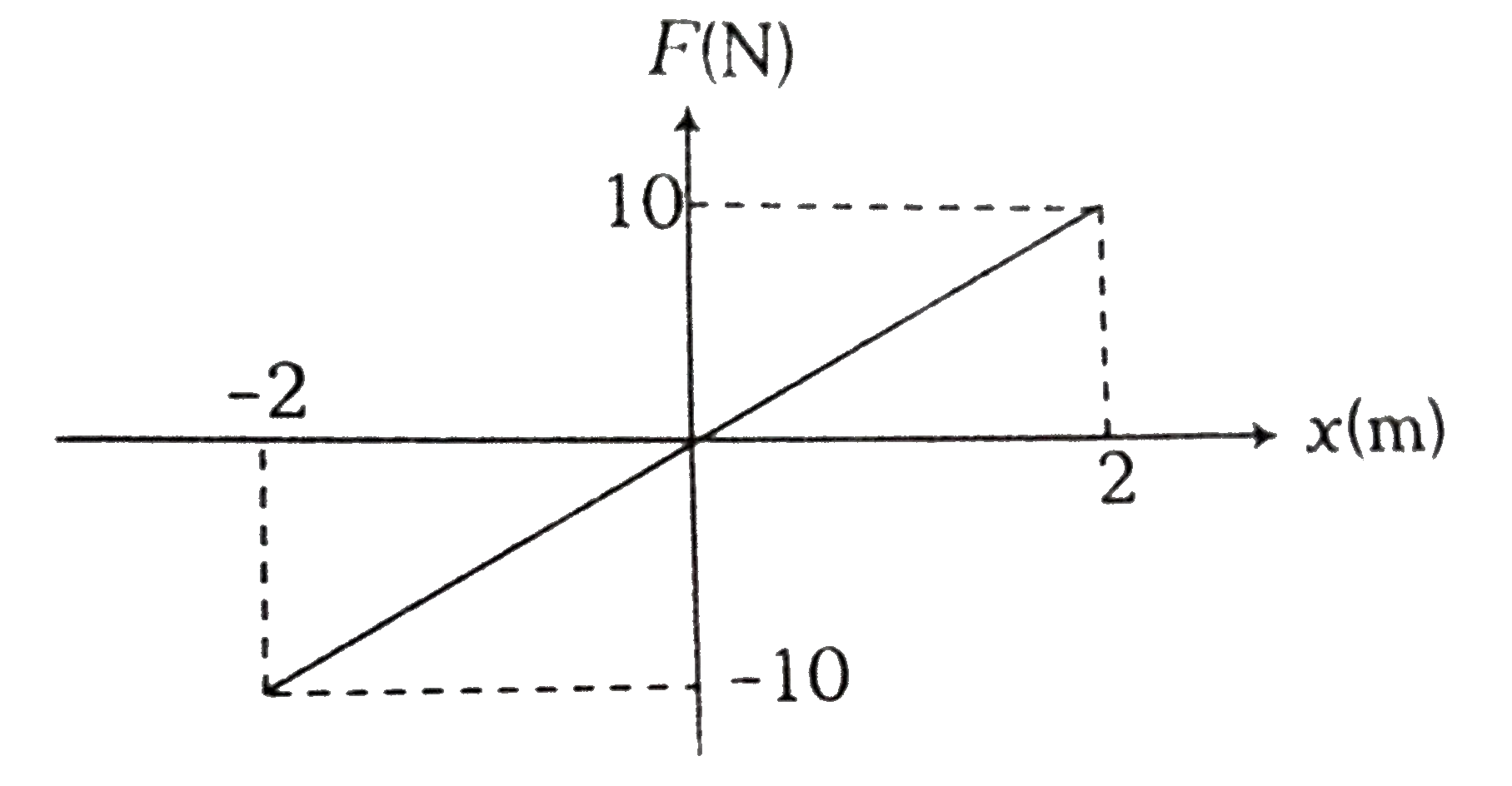
View SolutionA person says that he mesured the acceleration of a particle to be nonzero while no force was acting on the particle
View Solution

