If →F is force vector, →v is velocity , →a is acceleration vector and →r vector is displacement vector w.r.t. mean position than which of the following quantities are always non-negative in a simple harmonic motion along a straight line ?
→F.→a
→v.→r
→a.→r
→F.→r
The correct Answer is:A
To determine which quantities are always non-negative in simple harmonic motion (SHM) along a straight line, we need to analyze the given quantities: force vector (\overset{\vec}{F}), velocity vector (\overset{\vec}{v}), acceleration vector (\overset{\vec}{a}), and displacement vector (\overset{\vec}{r}) with respect to the mean position.
1. Understanding the Relationship in SHM:
- In SHM, the acceleration (\overset{\vec}{a}) is proportional to the negative of the displacement (\overset{\vec}{r}):
\overset{\vec}{a} = -\omega^2 \overset{\vec}{r}
- Here, ω is the angular frequency.
2. Analyzing the Acceleration:
- Since \overset{\vec}{a} = -\omega^2 \overset{\vec}{r}, the acceleration vector is always directed towards the mean position, and its magnitude is proportional to the distance from the mean position.
- The magnitude of acceleration (a) can be expressed as:
a=ω2r
- Thus, a2 is always non-negative since both ω2 and r2 are non-negative.
3. Analyzing the Force:
- The force in SHM is given by:
\overset{\vec}{F} = m \overset{\vec}{a} = -m \omega^2 \overset{\vec}{r}
- The force vector is also directed towards the mean position, and its magnitude is:
F=ma=mω2r
- The force is negative when considering the direction towards the mean position, thus it is not always non-negative.
4. Analyzing the Velocity:
- The velocity (\overset{\vec}{v}) can be either positive or negative depending on the direction of motion. Therefore, it is not always non-negative.
5. Analyzing the Dot Products:
- The dot product of the acceleration and itself:
\overset{\vec}{a} \cdot \overset{\vec}{a} = a^2
is always non-negative.
- The dot product of the force and acceleration:
\overset{\vec}{F} \cdot \overset{\vec}{a} = m \overset{\vec}{a} \cdot \overset{\vec}{a} = m a^2
is also always non-negative since m and a2 are non-negative.
6. Final Conclusion:
- The quantities that are always non-negative in simple harmonic motion are:
- \overset{\vec}{a} \cdot \overset{\vec}{a} (acceleration squared)
- \overset{\vec}{F} \cdot \overset{\vec}{a} (force dot acceleration)
Summary of Non-Negative Quantities:
- The quantities that are always non-negative in SHM are:
- a2 (acceleration squared)
- \overset{\vec}{F} \cdot \overset{\vec}{a} (force dot acceleration)
- In SHM, the acceleration (\overset{\vec}{a}) is proportional to the negative of the displacement (\overset{\vec}{r}):
\overset{\vec}{a} = -\omega^2 \overset{\vec}{r}
- Here, ω is the angular frequency.
- Since \overset{\vec}{a} = -\omega^2 \overset{\vec}{r}, the acceleration vector is always directed towards the mean position, and its magnitude is proportional to the distance from the mean position.
- The magnitude of acceleration (a) can be expressed as:
a=ω2r
- Thus, a2 is always non-negative since both ω2 and r2 are non-negative.
- The force in SHM is given by:
\overset{\vec}{F} = m \overset{\vec}{a} = -m \omega^2 \overset{\vec}{r}
- The force vector is also directed towards the mean position, and its magnitude is:
F=ma=mω2r
- The force is negative when considering the direction towards the mean position, thus it is not always non-negative.
- The velocity (\overset{\vec}{v}) can be either positive or negative depending on the direction of motion. Therefore, it is not always non-negative.
- The dot product of the acceleration and itself:
\overset{\vec}{a} \cdot \overset{\vec}{a} = a^2
is always non-negative.
- The dot product of the force and acceleration:
\overset{\vec}{F} \cdot \overset{\vec}{a} = m \overset{\vec}{a} \cdot \overset{\vec}{a} = m a^2
is also always non-negative since m and a2 are non-negative.
- The quantities that are always non-negative in simple harmonic motion are:
- \overset{\vec}{a} \cdot \overset{\vec}{a} (acceleration squared)
- \overset{\vec}{F} \cdot \overset{\vec}{a} (force dot acceleration)
- The quantities that are always non-negative in SHM are:
- a2 (acceleration squared)
- \overset{\vec}{F} \cdot \overset{\vec}{a} (force dot acceleration)
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 2, PART - I
26 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 2, PART - II
1 Video
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 1, PART - I
25 Videos
- SEMICONDUCTORSBOOK - RESONANCE ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Exercise 3
88 Videos
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PHYSICS
784 Videos
Similar Questions
Which of the following quantities is/are always non-negative in a simple harmonic motion along a straight line?
View SolutionSix vector →a through →f have the magnitudes and direction indicated in the figure. Which of the following statements is true?
View SolutionSix vector →a through →f have the magnitudes and direction indicated in the figure. Which of the following statements is true?
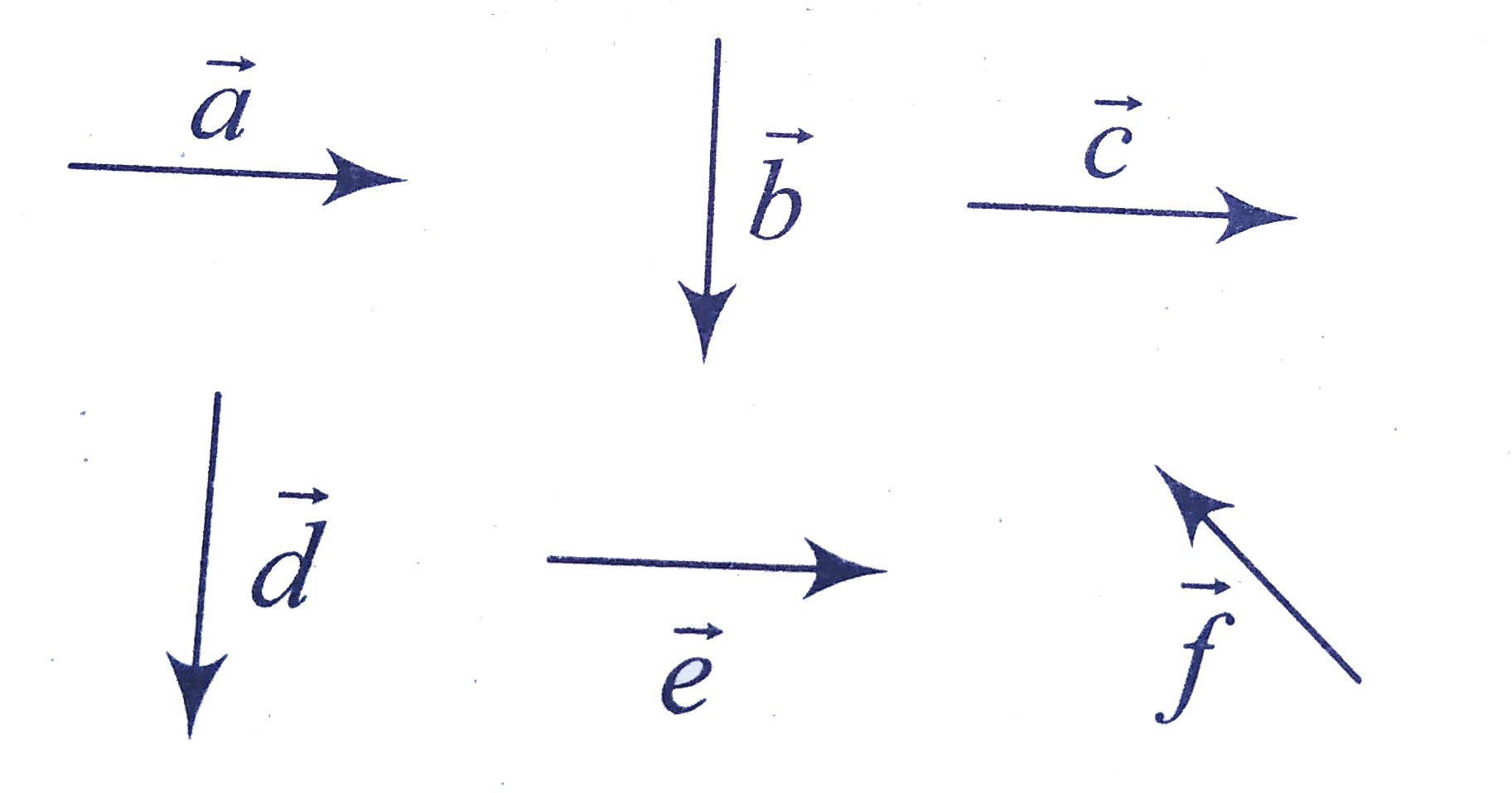
View SolutionIf →A and →B are two vectors of non-zero magnitude, which of the following relations cannot be possible ?
View SolutionA particle moves so that its position vector is given by →r=cosωtˆx+sinωtˆy, where ω is a constant which of the following is true ?
View SolutionA particle moves so that its position vector is given by →r=cosωtˆx+sinωtˆy, where ω is a constant which of the following is true ?
View SolutionA moving perticle of mass m is acted upon by five forces →F1,→F2,→F3,→F4 and →F5. Forces →F2 and →F3 are conservative and their potential energy funcations are U and W respectively. Speed of the particle changes from Va to Vb when it moves from position a to b. Choose the correct option :
View SolutionIf →a,→b,→c are non coplanar non-zero vectors such that →b×→c=→a,→a×→b=→c and →c×→a=→b , then which of the following is not true
View SolutionA straight line →r=→a+λ→b meets the plane →r.→n=0atp. Then position vector of P is
View SolutionTwo point masses 1 and 2 move with uniform velocities →v1 and →v2, respectively. Their initial position vectors are →r1 and →r2, respectively. Which of the following should be satisfied for the collision of the point masses?
View Solution

