A mass of 1kg attached to the bottom of a spring has a certain frequency of vibration. The following mass has to be added to it in order to reduce the frequency by half :
1kg
2kg
3kg
4kg
The correct Answer is:C
To solve the problem, we will follow these steps:
Step 1: Understand the formula for frequency
The frequency f of a mass-spring system is given by the formula:
f=12π√km
where k is the spring constant and m is the mass attached to the spring.
Step 2: Identify the initial conditions
In this case, the initial mass m1 is 1kg. Therefore, the initial frequency f1 can be expressed as:
f1=12π√k1=12π√k
Step 3: Determine the new frequency
We want to reduce the frequency to half of the initial frequency. Thus, the new frequency f2 is:
f2=f12=12(12π√k)=14π√k
Step 4: Relate the new frequency to the new mass
Using the frequency formula for the new mass m2, we have:
f2=12π√km2
Setting the two expressions for f2 equal gives:
14π√k=12π√km2
Step 5: Solve for the new mass
Cross-multiplying to eliminate the fractions:
√k=2√km2
Squaring both sides:
k=4km2
Dividing both sides by k (assuming k≠0):
1=4m2
Thus, solving for m2:
m2=4kg
Step 6: Determine the additional mass needed
Since the initial mass is 1kg, the additional mass ma that needs to be added is:
ma=m2−m1=4kg−1kg=3kg
Final Answer
The mass that needs to be added to reduce the frequency by half is 3 kg.
---
The frequency f of a mass-spring system is given by the formula:
f=12π√km
where k is the spring constant and m is the mass attached to the spring.
In this case, the initial mass m1 is 1kg. Therefore, the initial frequency f1 can be expressed as:
f1=12π√k1=12π√k
We want to reduce the frequency to half of the initial frequency. Thus, the new frequency f2 is:
f2=f12=12(12π√k)=14π√k
Using the frequency formula for the new mass m2, we have:
f2=12π√km2
Setting the two expressions for f2 equal gives:
14π√k=12π√km2
Cross-multiplying to eliminate the fractions:
√k=2√km2
Squaring both sides:
k=4km2
Dividing both sides by k (assuming k≠0):
1=4m2
Thus, solving for m2:
m2=4kg
Since the initial mass is 1kg, the additional mass ma that needs to be added is:
ma=m2−m1=4kg−1kg=3kg
The mass that needs to be added to reduce the frequency by half is 3 kg.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 2, PART - I
26 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 2, PART - II
1 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 1, PART - I
25 Videos
- SEMICONDUCTORSBOOK - RESONANCE ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Exercise 3
88 Videos
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PHYSICS
784 Videos
Similar Questions
A spring mass system oscillates with a frequency v. If it is taken in an elavator slowly accelerating upward, the frequency will
View SolutionA spring has natural length 40cm and spring constant 500N/m. A block of mass 1kg is attached at one end of the spring and other end of the spring is attached to a ceiling. The block is relesed from the position, where the spring has length 45cm.
View SolutionTwo masses of 1 kg and 5 kg are attached to the ends of a massless string passing over a pulley of negligible weight. The pulley itselt is attached to a light spring balance as shown in figure. The masses start moving during this interval, the readcing of spring balance will be-
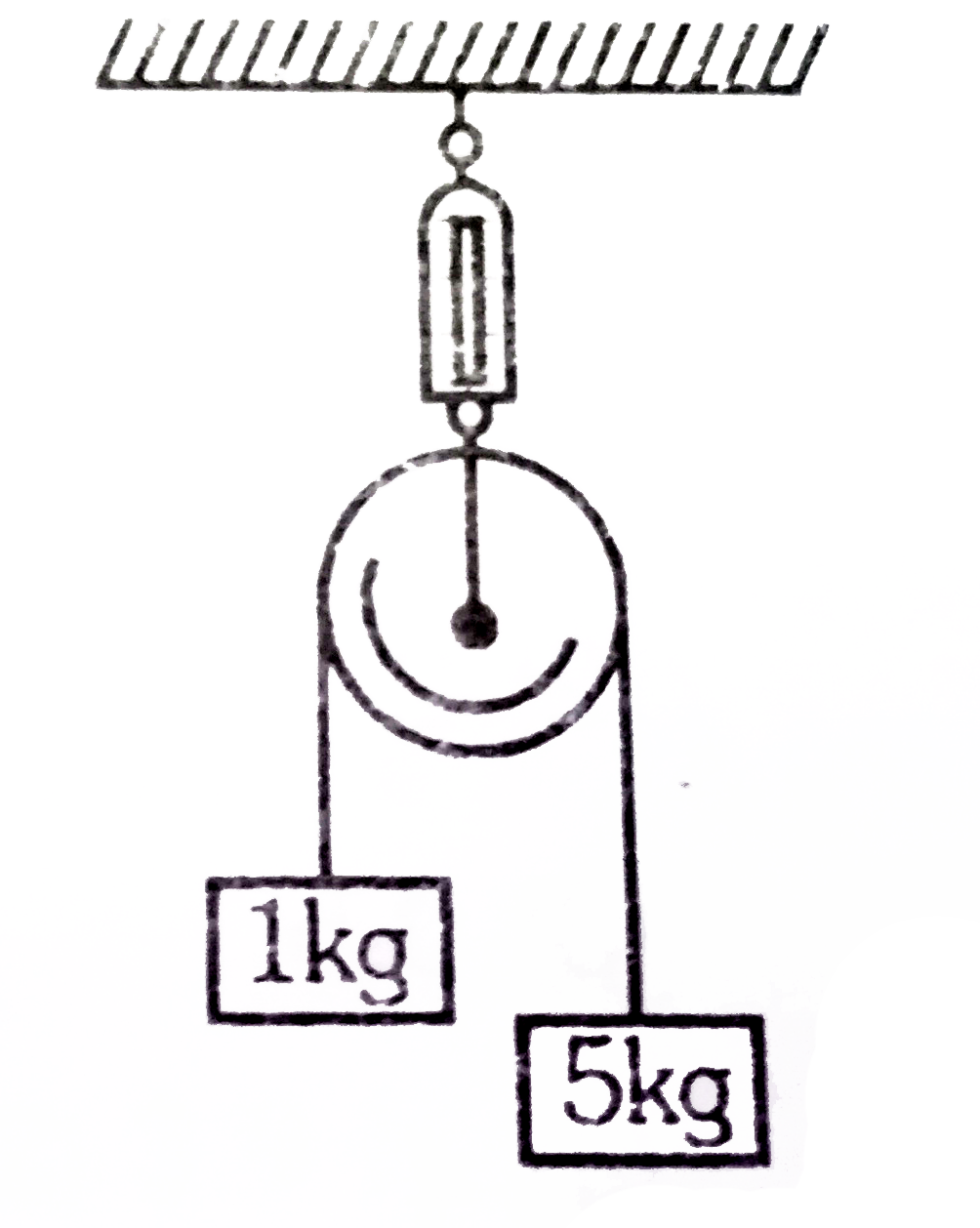
View SolutionTwo masses of 1 kg and 5 kg are attached to the ends of a massless string passing over a pulley of negligible weight. The pulley itselt is attached to a light spring balance as shown in figure. The masses start moving during this interval, the readcing of spring balance will be-
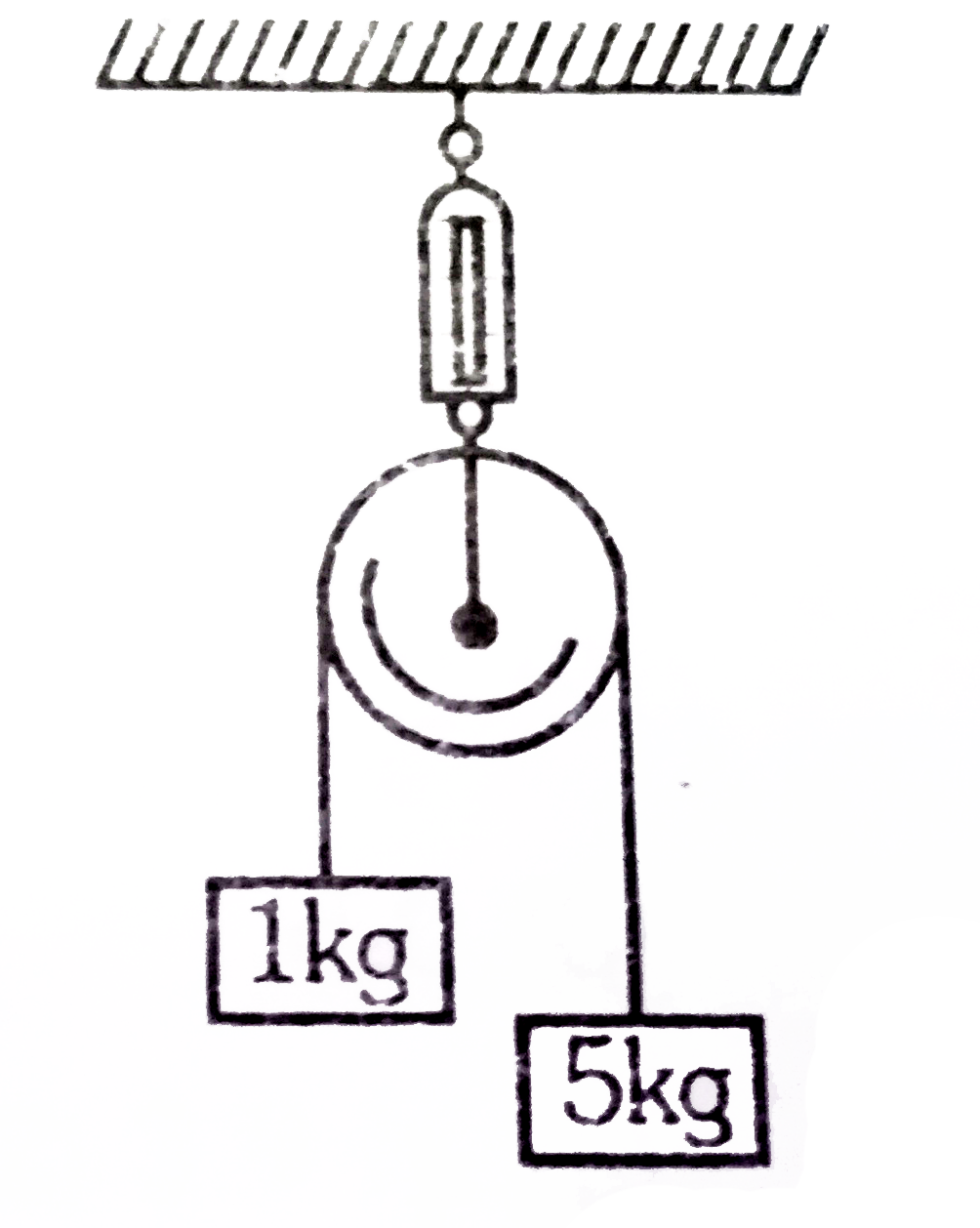
View SolutionA wire is attached to a pan of mass 200 g that contains a 2.0 kg mass as shown in the figure. When plucked, the wire vibrates at a fundamental frequency of 220 Hz. An additional unknown mass M is then added to the pan and a fundamental frequency of 260 Hz is detected. What is the value of M?
 .
.
View SolutionA 1 kg block attached to a spring vibrates with a frequency of 1 Hz on a frictionless horizontal table. Two springs identical to the original spring are attached in parallel to an 8 kg block placed on the same table. So, the frequency of vibration of the 8 kg block is
View SolutionA 1 kg block attached to a spring vibrates with a frequency of 1 Hz on a frictionless horizontal table. Two springs identical to the original spring are attached in parallel to an 8 kg block placed on the same table. So, the frequency of vibration of the 8 kg block is
View SolutionA spring of force constant 1200Nm−1 is mounted on a horizontal table as shown in figure. A mass of 3.0kg is attached to the free end of the spring, pulled side ways to a distance of 2.0cm and released. Determing.
(a) the frequency of oscillation of the mass.
(b) the maximum acceleration of the mass.
(c) the maximum speed of the mass.

View SolutionA spring of force constant 1200Nm−1 is mounted on a horizontal table as shown in figure. A mass of 3.0kg is attached to the free end of the spring, pulled side ways to a distance of 2.0cm and released. Determing.
(a) the frequency of oscillation of the mass.
(b) the maximum acceleration of the mass.
(c) the maximum speed of the mass.

View SolutionA object of mass m is suspended from a spring and it executes SHM with frequency n. If the mass is increased 4 times , the new frequency will be
View Solution
