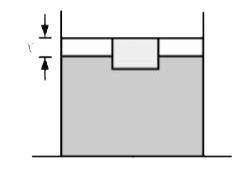
A solid cube floats in a liquid of density ρ with half of its volume submerged as shown. The side length of the cube is a, which is very small compared to the size of the container. Now a liquid of density ρ3 (immiscible with the liquid already in the container) is poured slowly into the container. The column of the liquid of density ρ3 that must be poured so that the cube is fully submerged (with its top surface coincident with the surface of the poured liquid) is :

a3
a2
2a3
3a4
The correct Answer is:D
Let the density of the cube be ρo
Then, because cube is in equilibrium ρoa3g=ρ(a32)g
⇒ρo=ρ2
Let the final equilibrium position of the cube be as shown
Then, ρoa3g=(ρ3)(a2x)g+ρ(a−x)(a2)g
⇒x=34a
Topper's Solved these Questions
- JEE MAIN - 5BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN - 5EXERCISE - PART I : PHYSICS (SECTION - 2)
5 Videos
- INTRODUCTION TO VECTORS & FORCES BOOK - VMC MODULES ENGLISHCHAPTER - INTRODUCTION TO VECTORS & FORCES EXERCISE - JEE Advanced ( ARCHIVE LEVEL-2)
12 Videos
- JEE MAIN REVISION TEST - 30 | JEE -2020BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST - 30 | JEE -2020EXERCISE - PHYSICS
25 Videos
Similar Questions
Knowledge Check
The pressure inside a liquid of density ρ at a depth h is :
AhρgBhρgChρgDhρA body floats in a liquid A of density ρ1 with a part of it submerged inside liquid while in liquid B of density ρ2 totally submerged inside liquid. The densities ρ1 and ρ2 are related as :
Aρ1=ρ2Bρ1<ρ2Cρ1>ρ2Dnothing can be said
The liquid inside the container has density ρ. Choose the correct option.
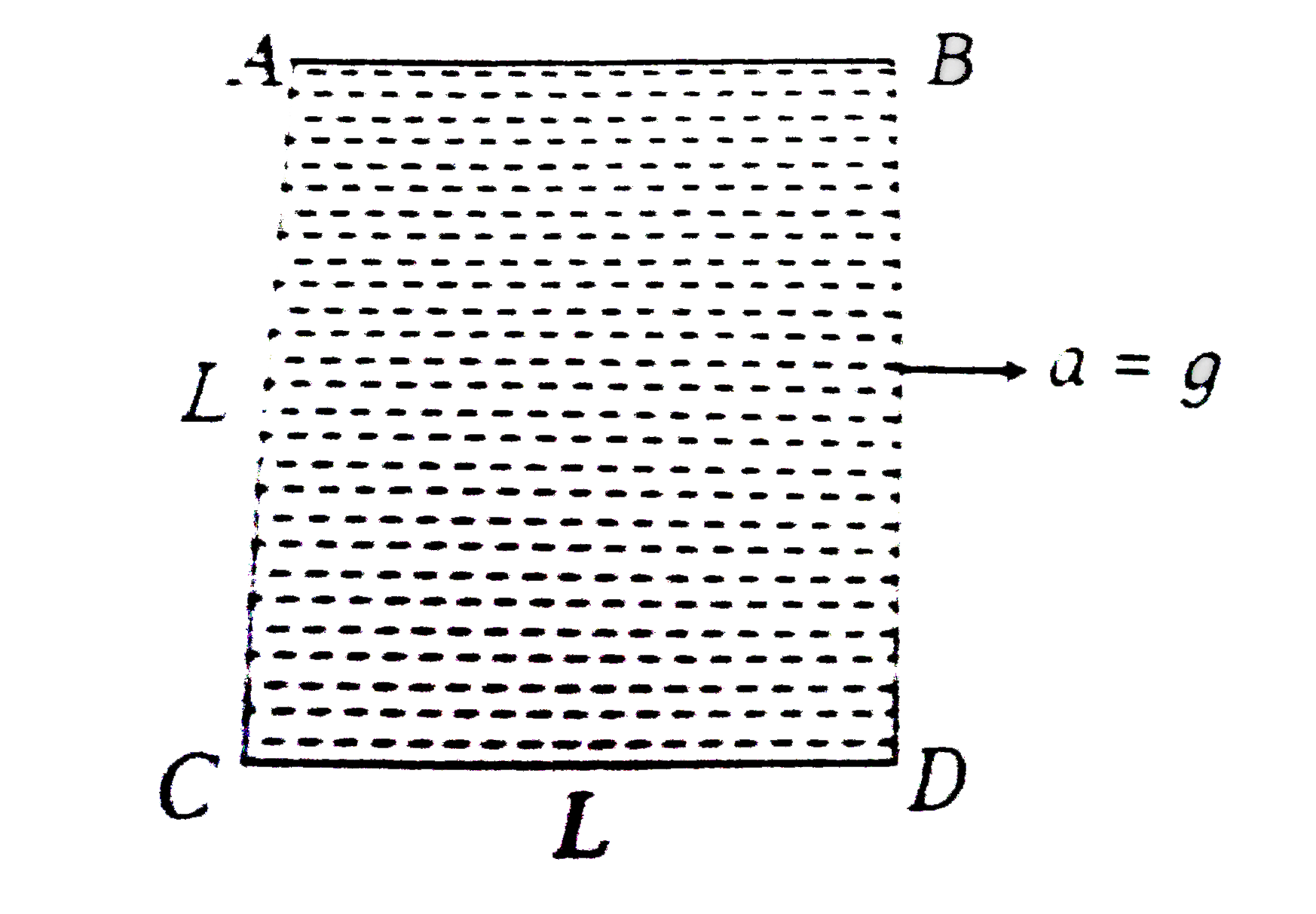
View SolutionIn a U-tube, two immiscible liquids of density ρ1andρ2 are arranged as shown in figure. The right part of the tube is closed at the top and some air is entrapped above liquid of density ρ2. The gauge pressure of this air is :

View SolutionA drop of liquid of density ρ is floating half-immersed in a liquid of density d. If σ is the surface tension the diameter of the drop of the liquid is
View SolutionA beaker containing a liquid of density ρ moves up with an acceleration a. The pressure due to the liquid at a depth h below the free surface of the liquid is.
View SolutionA solid cube of side a and density ρ0 floats on the surface of a liquid of density ρ. If the cube is slightly pushed downward, then it oscillates simple harmonically with a period of
View Solution
A sealed tank containing a liquid of density ρ moves with a horizontal acceleration a, as shown in the figure. The difference in pressure between the points A and B is
View Solution
