A drop of liquid of density ρ is floating half-immersed in a liquid of density d. If σ is the surface tension the diameter of the drop of the liquid is
√σg(2ρ−d)
√2σg(2ρ−d)
√6σg(2ρ−d)
√12σg(2ρ−d)
The correct Answer is:D
To find the diameter of a drop of liquid of density ρ that is floating half-immersed in another liquid of density d, we can follow these steps:
1. Understanding Forces Acting on the Drop:
- The drop is floating half-immersed, which means that the weight of the drop is balanced by the buoyant force and the surface tension force acting on the drop.
- The forces acting on the drop are:
- Weight of the drop (mg) acting downwards.
- Buoyant force (Fb) acting upwards.
- Surface tension force (Fs) acting upwards.
2. Weight of the Drop:
- The weight of the drop can be expressed as:
mg=ρVg
- Here, V is the volume of the drop.
3. Volume of the Drop:
- The volume V of a sphere is given by:
V=43πr3
- Since the drop is half-immersed, the volume submerged is half of the total volume:
Vsubmerged=12V=23πr3
4. Buoyant Force:
- The buoyant force can be calculated using Archimedes' principle:
Fb=d⋅Vsubmerged⋅g=d⋅(23πr3)g
5. Surface Tension Force:
- The surface tension force is given by:
Fs=σ⋅L
- The length L in contact with the liquid is the circumference of the drop at the water surface, which is 2πr:
Fs=σ⋅(2πr)
6. Setting Up the Equation:
- Since the drop is floating, the weight is equal to the sum of the buoyant force and the surface tension force:
mg=Fb+Fs
- Substituting the expressions we derived:
ρ⋅(43πr3)g=d⋅(23πr3)g+σ⋅(2πr)
7. Simplifying the Equation:
- Cancel g and 23πr3 from both sides:
ρ⋅43=d+3σr
- Rearranging gives:
3σr=ρ⋅43−d
8. Solving for r:
- Rearranging for r:
r=3σρ⋅43−d
9. Finding the Diameter:
- The diameter D of the drop is given by:
D=2r=2⋅3σρ⋅43−d=6σρ⋅43−d
Final Expression for Diameter:
D=6σρ⋅43−d
- The drop is floating half-immersed, which means that the weight of the drop is balanced by the buoyant force and the surface tension force acting on the drop.
- The forces acting on the drop are:
- Weight of the drop (mg) acting downwards.
- Buoyant force (Fb) acting upwards.
- Surface tension force (Fs) acting upwards.
- The weight of the drop can be expressed as:
mg=ρVg
- Here, V is the volume of the drop.
- The volume V of a sphere is given by:
V=43πr3
- Since the drop is half-immersed, the volume submerged is half of the total volume:
Vsubmerged=12V=23πr3
- The buoyant force can be calculated using Archimedes' principle:
Fb=d⋅Vsubmerged⋅g=d⋅(23πr3)g
- The surface tension force is given by:
Fs=σ⋅L
- The length L in contact with the liquid is the circumference of the drop at the water surface, which is 2πr:
Fs=σ⋅(2πr)
- Since the drop is floating, the weight is equal to the sum of the buoyant force and the surface tension force:
mg=Fb+Fs
- Substituting the expressions we derived:
ρ⋅(43πr3)g=d⋅(23πr3)g+σ⋅(2πr)
- Cancel g and 23πr3 from both sides:
ρ⋅43=d+3σr
- Rearranging gives:
3σr=ρ⋅43−d
- Rearranging for r:
r=3σρ⋅43−d
- The diameter D of the drop is given by:
D=2r=2⋅3σρ⋅43−d=6σρ⋅43−d
D=6σρ⋅43−d
Topper's Solved these Questions
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Multiple Correct
17 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Assertion- Reasoning
13 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Subjective
16 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
Similar Questions
A solid of density D is floating in a liquid of density d. If υ is the volume of solid submerged in the liquid and V is the total volume of the solid, then υ/V equal to
View SolutionAn object of mass m is floating in a liquid of density σ. If the object is made up of density ρ, then appare weight of the object in the liquid is
View Solution
Knowledge Check
The pressure inside a liquid of density ρ at a depth h is :
AhρgBhρgChρgDhρ
A sphere of density ρ is half submerged in a liquid of density σ and surface tension T. The sphere remains in equilibrium. Find radius of the sphere (assume the force due to surface tension acts tangentially to surface of sphere)
View SolutionAn object of w and density ρ is submerged in liquid of density σ, its apparent weight will be
View SolutionA small ball of density ρ is immersed in a liquid of density σ(>ρ) to a depth h and released. The height above the surface of water up to which the ball will jump is
View Solution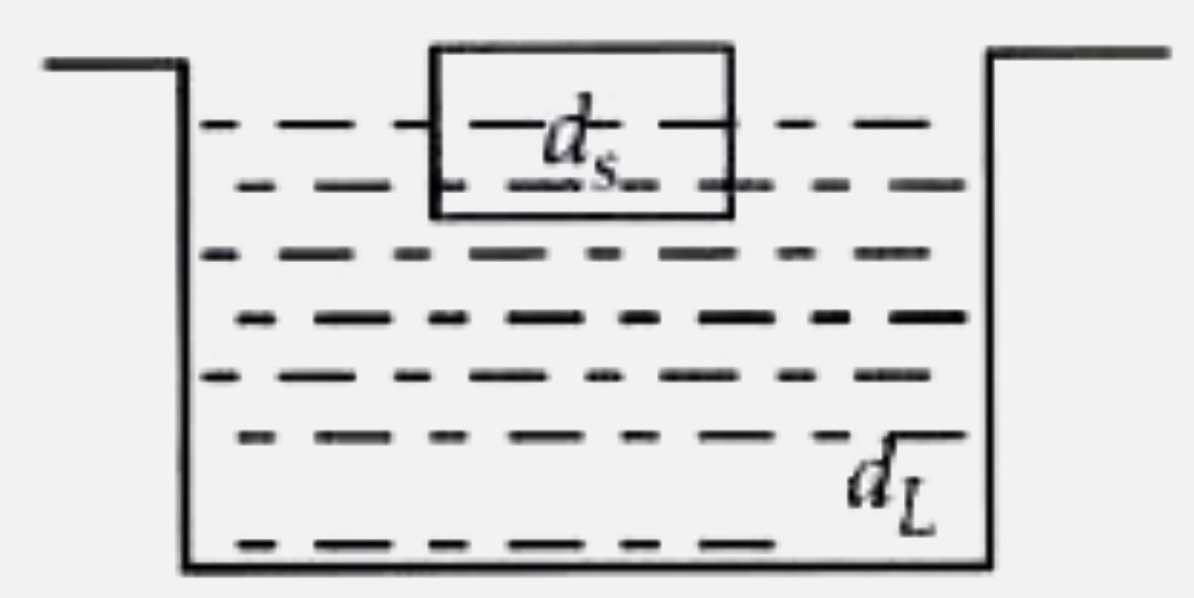
The figure above shows a solid of density dS floating in a liquid of density dL.
What is the apparent weight of the floating body?
View SolutionA body of density ρ sinks in a liquid of density ρL.The densities ρ and ρL are related as:
View SolutionA block of density ρ floats in a liquid with its one third volume immersed. The density of the liquid is
View SolutionA body of density ρ is immersed in a liquid of density ρL.State condition when the body will (i) float (ii) sink in liquid.
View Solution
