A particle start form mean position and moves towards positive extreme as shown. Find the equation of the SHM. Amplitude of SHM is A.

General equation of SHM can be written as x=Asin(ωt+ϕ)
At t=0,x=0
∴0=Asinϕ
∴Φ=0,π,ϕ∈[0,2π)
Also, at t=0,v=+ve
∴Aωcosϕ=+ve
or, ϕ=0
Hence, if the particle is at mean position at t=0 and is moving towards +ve extreme, then the equation of SHM is given by x=Asinωt
Similarly
for ϕ=π
∴ equation of SHM is x=A(ωt+π)
or, x=−Asinωt

Topper's Solved these Questions
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Solved Miscellaneous Problems
9 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Board Level Exercise
24 Videos
- SEMICONDUCTORSBOOK - RESONANCE ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Exercise 3
88 Videos
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PHYSICS
784 Videos
Similar Questions
A particle starts from point x=−√32A and move towards negative extreme as shown,
_S01_011_Q01.png)
(a) Find the equation of the SHM
(b) Find the time taken by the particle to go directly from its initial position to negative extreme.
(c) Find the time taken by the particle to reach at mean position.
View SolutionA particle starts from a point P at a distance of A/2 from the mean position O and travels towards left as shown in the figure. If the time period of SHM, executed about O is T and amplitude A then the equation of the motion of particle is

View SolutionIf time of mean position from amplitude (extreme) position is 6 s. then the frequency of SHM will be :
View SolutionA particle executing SHM of amplitude 4 cm and T=4s .The time taken by it to move from positive extreme position to half the amplitude is
View SolutionA particle executes SHM from extreme position and covers a distance equal to half to its amplitude in 1 s. find out it's Time Period.
View SolutionBlock A of mass m is performing SHM of amplitude a. Another block B of mas m is gently placed on A when it passes through mean position and B sticks to A. Find the time period and amplitude of new SHM.
View SolutionPotential energy of a particle at mean position is 4 J and at extreme position is 20 J. Given that amplitude of oscillation is A. Match the following two columns

View SolutionTwo particles A and B oscillates in SHM having same amplitude and frequencies fA and fB respectively. At t=0 the particle A is at positive extreme position while the particle B is at a distance half of the amplitude on the positive side of the mean position and is moving away from the mean position.
View SolutionA partical excutes SHM with amplitudeA and angular frequency ω. At an instant the particle is at a distance A/5 from the mean position and is moving away from it. Find the time after which it will come back to this position again and also find the time after which it will pass through the mean position.
View SolutionA particle is performing SHM about mean position O as shown in the figure given below. Its amplitude is 5 m and time period of oscillation is 4 s. The minimum time taken by the particle to move from point A to B is nearly
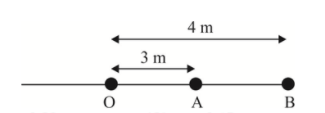
View Solution
