Block A of mass m is performing SHM of amplitude a. Another block B of mas m is gently placed on A when it passes through mean position and B sticks to A. Find the time period and amplitude of new SHM.
To solve the problem, we need to find the new time period and amplitude of the simple harmonic motion (SHM) after block B is placed on block A.
1. Understanding the Initial Conditions:
- Block A has a mass m and performs SHM with an amplitude a.
- The time period T of block A can be expressed as:
T=2π√mk
where k is the spring constant.
2. Effect of Adding Block B:
- When block B (also of mass m) is placed on block A at the mean position, the total mass becomes 2m.
- The new time period T′ for the combined system is given by:
T′=2π√2mk
3. Finding the New Time Period:
- The new time period can be simplified as:
T′=2π√2k/m=√2⋅T
Thus, the new time period is √2 times the original time period.
4. Finding the New Amplitude:
- At the mean position, the velocity of block A is maximum and can be expressed as:
v=ωa=√kma
- When block B is placed on block A, the momentum is conserved. The initial momentum of block A is mv and the final momentum of the combined mass is (2m)v′:
mv=(2m)v′⟹v′=v2
- The new amplitude a′ can be found using the relationship between velocity and amplitude:
v′=ω′a′
where ω′=√k2m. Substituting v′:
v2=√k2ma′
5. Relating the New Amplitude to the Original Amplitude:
- Substitute v=√kma:
12√kma=√k2ma′
- Squaring both sides and simplifying gives:
14kma2=k2ma′2
- Canceling k/m from both sides:
14a2=12a′2⟹a′2=12a2⋅4=2a2⟹a′=√2a
Final Results:
- The new time period T′ is:
T′=√2T
- The new amplitude a′ is:
a′=√2a
- Block A has a mass m and performs SHM with an amplitude a.
- The time period T of block A can be expressed as:
T=2π√mk
where k is the spring constant.
- When block B (also of mass m) is placed on block A at the mean position, the total mass becomes 2m.
- The new time period T′ for the combined system is given by:
T′=2π√2mk
- The new time period can be simplified as:
T′=2π√2k/m=√2⋅T
Thus, the new time period is √2 times the original time period.
- At the mean position, the velocity of block A is maximum and can be expressed as:
v=ωa=√kma
- When block B is placed on block A, the momentum is conserved. The initial momentum of block A is mv and the final momentum of the combined mass is (2m)v′:
mv=(2m)v′⟹v′=v2
- The new amplitude a′ can be found using the relationship between velocity and amplitude:
v′=ω′a′
where ω′=√k2m. Substituting v′:
v2=√k2ma′
- Substitute v=√kma:
12√kma=√k2ma′
- Squaring both sides and simplifying gives:
14kma2=k2ma′2
- Canceling k/m from both sides:
14a2=12a′2⟹a′2=12a2⋅4=2a2⟹a′=√2a
- The new time period T′ is:
T′=√2T
- The new amplitude a′ is:
a′=√2a
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Board Level Exercise
24 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 1, PART - I
25 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- SEMICONDUCTORSBOOK - RESONANCE ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Exercise 3
88 Videos
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PHYSICS
784 Videos
Similar Questions
A 1kg block is executing simple harmonic motion of amplitude 0.1m on a smooth horizontal surface under the restoring force of a spring of spring constant 100N/m. A block of mass 3kg is gently placed on it at the instant it passes through the mean position. Assuming that the two blocks move together. Find the frequency and the amplitude of the motion.
View SolutionA 1kg block is executing simple harmonic motion of amplitude 0.1m on a smooth horizontal surface under the restoring force of a spring of spring constant 100N/m. A block of mass 3kg is gently placed on it at the instant it passes through the mean position. Assuming that the two blocks move together. Find the frequency and the amplitude of the motion.
View SolutionBlock of mass m2 is in equilibrium as shown in figure. Anotherblock of mass m1 is kept gently on m2. Find the time period of oscillation and amplitude.
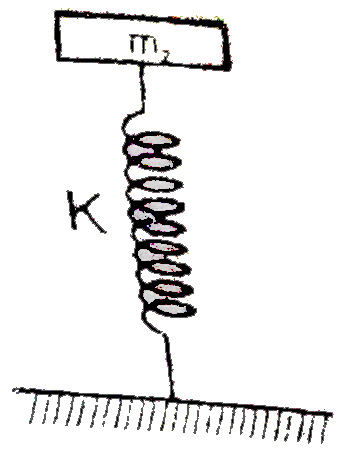
View SolutionBlock of mass m2 is in equilibrium as shown in figure. Anotherblock of mass m1 is kept gently on m2. Find the time period of oscillation and amplitude.
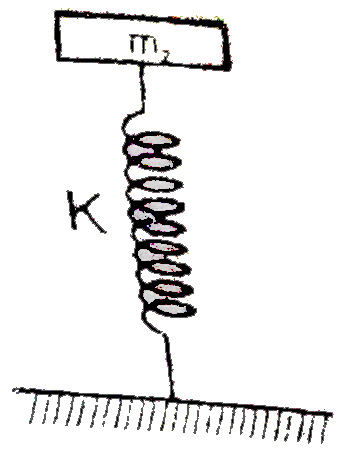
View SolutionA particle executes shm in a line 10 cm long. When it passes through the mean position its velocity is 15cms−1 . Find the period.
View SolutionThe kinetic energy of a particle executing shm is 32 J when it passes through the mean position. If the mass of the particle is.4 kg and the amplitude is one metre, find its time period.
View SolutionA body of mass 8 kg performs S.H.M. of amplitude 60 cm. The restoring force is 120 N, when the displacement is 60 cm. The time period is
View SolutionA block of mass m attached to a massless spring is performing oscillatory motion of amplitude A on a frictionless horizontal plane. If half of the mass of the block off when it is passing through its mean position, the amplitude of oscillation for the remaining system become fA. The value of f is .
View SolutionA particle is performing SHM of amplitude 'A' and time period 'T'. Find the time taken by the particle to go from 0→A/2.
View SolutionA bob executes shm of period 20 s. Its velocity is found to be 0.05ms−1 after 2 s when it has passed through its mean position. Find the amplitude of the bob.
View Solution
