If time of mean position from amplitude (extreme) position is 6 s. then the frequency of SHM will be :
0.01 Hz
0.02 Hz
0.03 Hz
0.04 Hz
The correct Answer is:D
To find the frequency of Simple Harmonic Motion (SHM) given that the time from the mean position to the extreme position is 6 seconds, we can follow these steps:
1. Understanding the Motion: In SHM, the motion can be visualized as oscillating between two extreme positions (amplitudes) and passing through a mean position. The time taken to move from one extreme position to the mean position is a quarter of the total time period (T) of the motion.
2. Setting Up the Equation: Given that the time from the mean position to the extreme position is 6 seconds, we can denote this time as t/4, where t is the total time period of the motion. Thus, we have:
t4=6 seconds
3. Calculating the Total Time Period (T): To find the total time period t, we can rearrange the equation:
t=6×4=24 seconds
4. Finding the Frequency (f): The frequency f of SHM is defined as the reciprocal of the time period:
f=1t
Substituting the value of t:
f=124 Hz
5. Calculating the Frequency: Performing the calculation:
f=0.04167 Hz≈0.04 Hz
Final Answer:
The frequency of SHM is approximately 0.04 Hz.
---
t4=6 seconds
t=6×4=24 seconds
f=1t
Substituting the value of t:
f=124 Hz
f=0.04167 Hz≈0.04 Hz
The frequency of SHM is approximately 0.04 Hz.
Similar Questions
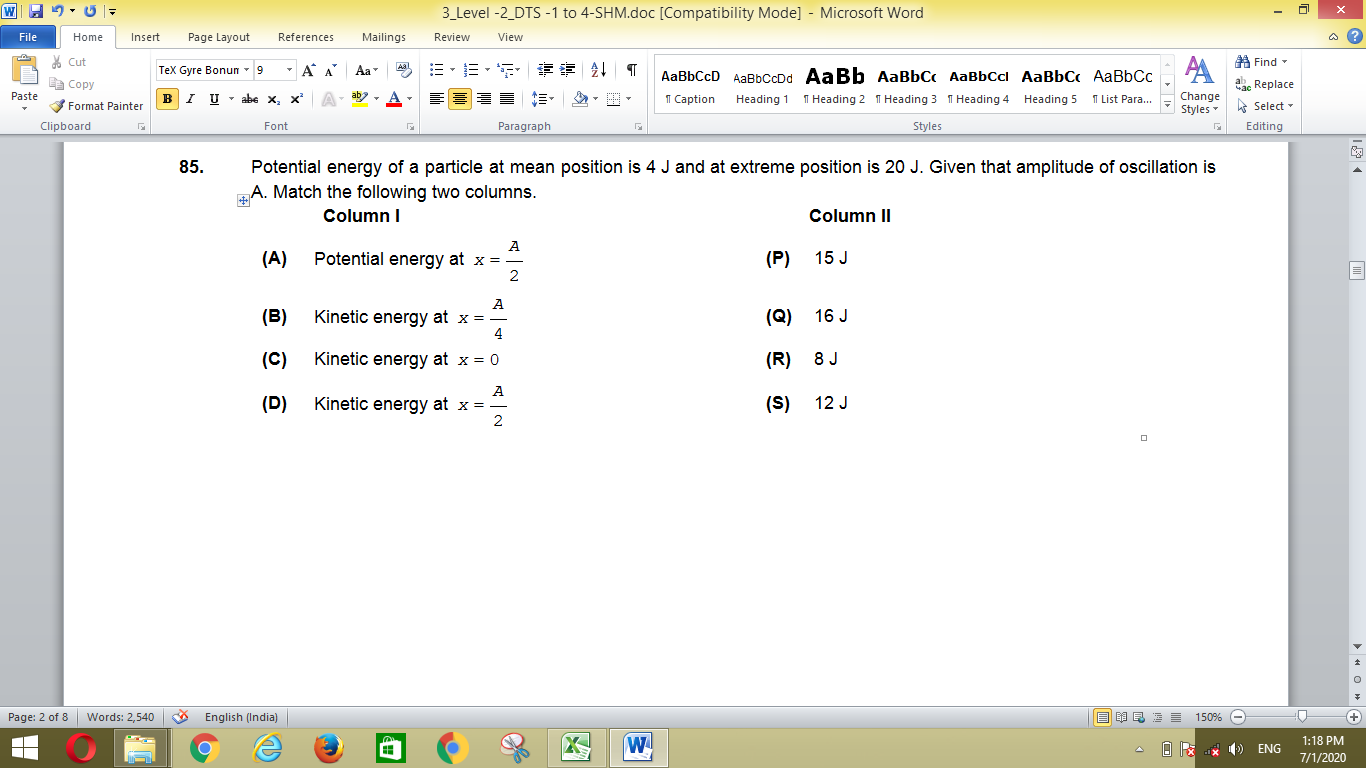
Potential energy of a particle at mean position is 4 J and at extreme position is 20 J. Given that amplitude of oscillation is A. Match the following two columns
 View Solution
View SolutionA particle on a stretched string supporting a travelling wave, takess 5.0s to move from its mean position to the extreme position. The distance between two consecutive particle, which are at their mean position, is 3.0cm. Find the wave speed (∈m/s).
View Solution
Knowledge Check
- Question 1 - Select One
The kinetic energy of a particle, executing S.H.M. is 16 J when it is in its mean position. IF the amplitude of oscillation is 25 cm and the mass of the particle is 5.12 Kg, the time period of its oscillations is
Aπ/5 secB2πsecC20πsecD5π sec
A particle on a stretched string supporting a travelling wave, takes 5.0 ms to move from its mean position to the extreme position. The distance between two consecutive particles, which are at their mean positions, is 2.0 cm. Find the frequency, the wavelength and the wave speed.
View SolutionA particle start form mean position and moves towards positive extreme as shown. Find the equation of the SHM. Amplitude of SHM is A.
 View Solution
View SolutionThe force on a body executing SHM is 4 N when the displacement from mean position is 2 cm. If amplitude of oscillation is 10 cm, then the maximum kinetic energy associated with the SHM will be
View SolutionTwo particles P1 and P2 are performing SHM along the same line about the same mean position , initial they are at their extreme position. If the time period of each particle is 12 sec and the difference of their amplitude is 12cm then find the minimum time after which the separation between the particle becomes 6cm.
View SolutionIn a shm, what is the minimum time required for a particle to move between two points 10 cm on either side of the mean position ? The amplitude and time period of the particle are 20 cm and 2 seconds respectively.
View SolutionA particle executes linear SHM with amplitude A and mean position is x=0. Determine position of the particle where potential energy of the particle is equal to its kinetic energy.
View SolutionA particle executes simple harmonic motion with an amplitude of 4cm At the mean position the velocity of the particle is 10cm/s. distance of the particle from the mean position when its speed 5 cm/s is
View Solution
