Two very large open tanks A&F both contain the same liquid. A horizontal pipe BCD, having a small constriction at C, leads out of the bottom of tank A, and a vertical pipe E containing air opens into the constriction at C and dips into the liquid in tank F. Assume stremline flow and no viscosity. If the cross section area at C is one-half that at D, and if D is at distance h1 below the level of the liquid in A, to what height h2 will liquid rise in pipe E? Express your answer in terms of h1.
[Neglect changes in atmosphere pressure with elevation. In the containers there is atmosphere above the water surface and D is also open to atmosphere.]
![Two very large open tanks A & F both contain the same liquid. A horizontal pipe BCD, having a small constriction at C, leads out of the bottom of tank A, and a vertical pipe E containing air opens into the constriction at C and dips into the liquid in tank F. Assume stremline flow and no viscosity. If the cross section area at C is one-half that at D, and if D is at distance h(1) below the level of the liquid in A, to what height h(2) will liquid rise in pipe E? Express your answer in terms of h(1). [Neglect changes in atmosphere pressure with elevation. In the containers there is atmosphere above the water surface and D is also open to atmosphere.]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/RES_WFPM_PHY_XI_C01_E01_127_Q01.png)
The correct Answer is:h2=3h1
Apply Bernolli's equation b/w point P & D
Patm+ρgh1+12ρV2P=Patm+ρg(o)+12ρv2D
[Assume zero level D]
Vp≈0 Area of cross section is very large
VD=√2gh1
Since area at C is half than area at D
so according to continuity equation
VCAC=VDAD⇒VC=2VD=2√2gh1
Now for point P & C according to Bernolli's equation.
PP+ρgh1+12ρV2p=PC+ρg(0)+12ρ.V2C
VP≈0
⇒Patm+ρgh1=PC+12ρ.(2√2gh1)2
⇒Patm=PC+3ρgh1....(i)
for point E
PE=PC+ρgh2=Patm
from (i) & (ii)
3ρgh1=ρgh2
⇒h2=3h1
Topper's Solved these Questions
Similar Questions
An organ pipe, open at both ends, contains
View SolutionThe pressure at the bottom of a tank of liquid is not proprtional to
View SolutionThere is a small hole near the botton of an open tank filled with liquid. The speed of the water ejected does not depend on
View SolutionA non viscous inconpressible liquid is flowing from a horizontal pipe of non-uniform cross section as shown, Choose the correct option
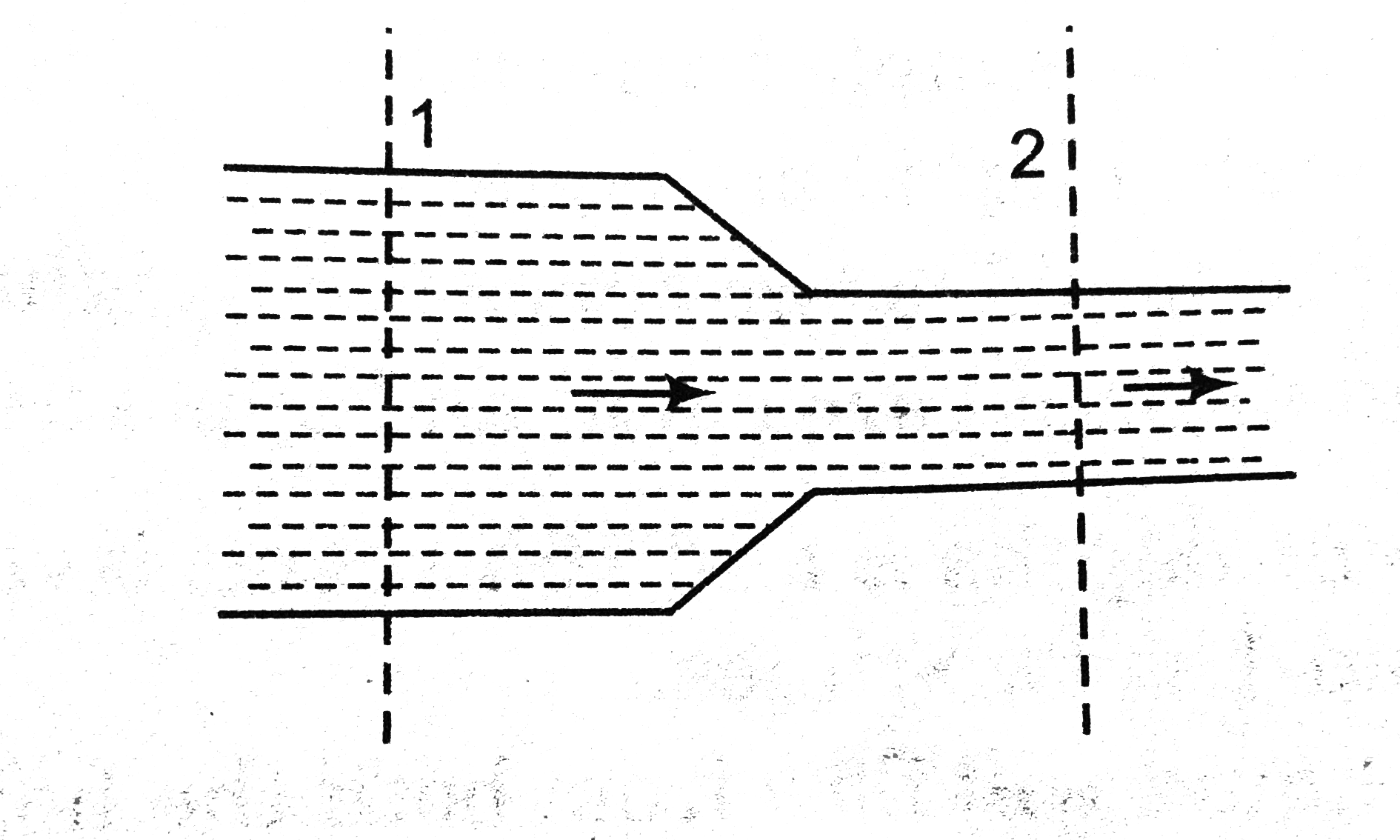
View Solution
A sealed tank containing a liquid of density ρ moves with a horizontal acceleration a, as shown in the figure. The difference in pressure between the points A and B is
View SolutionA sealed tank containing a liquid of density ρ moves with horizontal acceleration a as shown in the figure. The difference in pressure between two points A and B will be

View SolutionA large open top container of negligible mass and uniform cross sectional area A a has a small hole of cross sectional area A/100 in its side wall near the bottom. The container is kept on a smooth horizontal floor and contains a liquid of density ρ and mass M0. Assuming that the liquid starts flowing out horizontally through the hole at t=0, calculate a the acceleration of the container and its velocity when 75% of the liquid has drained out.
View SolutionA horizontal pipe of shown cross - section has a liquid flowing through it and follows Bernouli's theorem . Which of the following is/are constant through out pipe ?
View SolutionA horizontal pipe of area of cross-section a and 3a respectively, then the ratio of velocity of flow at two different cross-section (If flow is streamline) is
View SolutionThe pipe shows the volume flow rate of an ideal liquid at certain time and its direction. What is the value of Q in m3/s? (Assume steady state and equal area of cross section at each opening)

View Solution

