A particle moving on x - axis has potential energy joule along x - axis. The particle is relesed at . The maximum value of will be ( is in metre)
5m
3m
7m
8m
The correct Answer is:C
At equilibrium position , F=0
Since particle is released at x=-3, therefore amplitude of particle is 5.
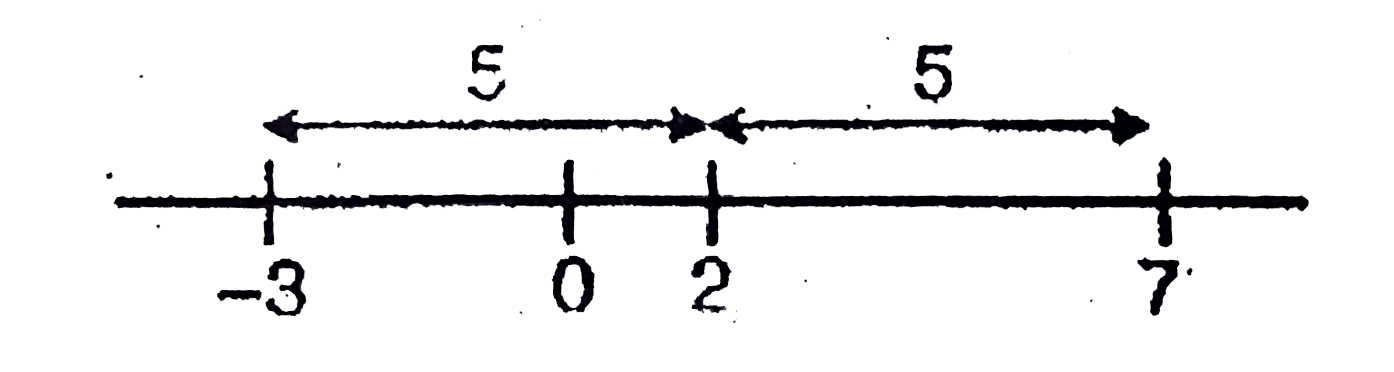
It will oscillate about x=2 with an amplitude of 5.
maximum value of x will be 7.
Topper's Solved these Questions
Similar Questions
A particle moves along the X-axis as x=u(t−2s)+a(t−2s)2.
View SolutionA particle moves along the X-axis as x=u(t−2s)=at(t−2)2.
View SolutionPosition of particle moving along x-axis is given as x=2+5t+7t2 then calculate :
View SolutionA particle is moving along the x-axis with an acceleration a = 2x where a is in ms–2andx is in metre. If the particle starts from rest at x=1 m, find its velocity when it reaches the position x = 3.
View SolutionVelocity of particle moving along x-axis is given as v=(x3−x2+2) m/sec. Find the acceleration of particle at x=2 meter.
View SolutionFor a particle moving along x−axis, speed must be increasing for the following graph :
View SolutionA particle of mass 4 kg moves along x axis, potential energy ( U ) varies with respect to x as U=20+(x−4)2 , maximum speed of paritcle is at
View SolutionA particle is moving along the x-axis whose acceleration is given by a=3x−4, where x is the location of the particle. At t = 0, the particle is at rest at x=4/3m. The distance travelled by the particles in 5 s is
View SolutionA particle is moving along x-axis. Its velocity v with x co-ordinate is varying as v=√x. Then
View SolutionA single conservative fore Fx acts on a 2kg particle that moves along the x-axis. The potential energy is given by.
U=(x−4)2−16
Here, x is in metre and U in joule. At x=6.0m kinetic energy of particle is 8J find .
(a) total mechanical energy
(b) maximum kinetic energy
(c) values of x between which particle moves
(d) the equation of Fx as a funcation is zero
(e) the value of x at which Fx is zero .
View Solution
