When a composite wire is made by joining tow wires as shown in figure and possible frequencies of this wire is asked (both ends fixed) then the lowest frequency is that at which individual lowest frequencies of the two wires are equal. 
In the figure ,l1=l2=l μ1=μ29=mu. The tension in the strings is T. Here μis the mass per unit length.
What is the lowest frequency such that the junction is an antinode?
14l√lμ
34l√lμ
54l√lμ
74l√lμ
The correct Answer is:A
For antinode
f1=(2n1−1)4l√lμ
f2=(2n2−1)4l√l9μ=(2n2−1)12l√lμ
f=14l√lμ(2n1−1)4l=2n2−112l
6n1−3=2n2−1
6n1−2n2=2 n1=1,n2=2
3n1−n2=1,
Topper's Solved these Questions
Similar Questions
A composite wire is made by joining two uniform wires. If l1=l2=l and μ1=μ29=μ. Tension in the strings is T , μ is mass per unit length. Then lowest frequency such that the junction is an antinode.

View SolutionA composite wire is made by joining two uniform wires. If l1=l2=l and μ1=μ29=μ. Tension in the strings is T , μ is mass per unit length. Then lowest frequency such that the junction is an antinode.

View SolutionThe frequency (f) of a stretched string depends upen the tension F (dimensions of form ) of the string and the mass per unit length mu of string .Derive the formula for frequency
View SolutionFundamental frequency of a sonometer wire is n. If
the length and diameter of the wire are doubled
keeping the tension same, then the new fundamental
frequency is
View SolutionFundamental frequency of sonometer wire is n. If the length, tension and diameter of wire are tripled the new fundamental frequency is
View SolutionThe fundamental frequency of a sonometer wire is n . If length tension and diameter of wire are triple then the new fundamental frequency is.
View SolutionA current carrying wire is bent in the L shapes as shown in figure. The length of both arms extend to infinity. Then, the magnetic field at O is-
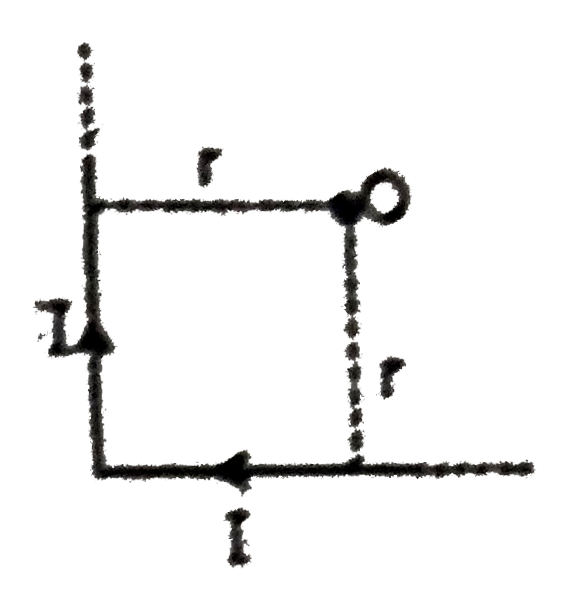
View SolutionTwo different stretched wires have same tension and mass per unit length. Fifth overtone frequency of the first wire is equal to second harmonic frequency of the second wire. Find the ratio of their lengths.
View SolutionA sonometer wire has a total length of 1 m between the fixed ends. Where should the two bridges be placed below the wire so that the three segments of the wire have their fundamental frequencies in the ratio 1 : 2 : 3 ?
View SolutionTwo wires are in unison. If the tension in one of the wires is increased by 2%, 5 beats are produced per second. The initial frequency of each wire is
View Solution

