A current carrying wire is bent in the L shapes as shown in figure. The length of both arms extend to infinity. Then, the magnetic field at O is-
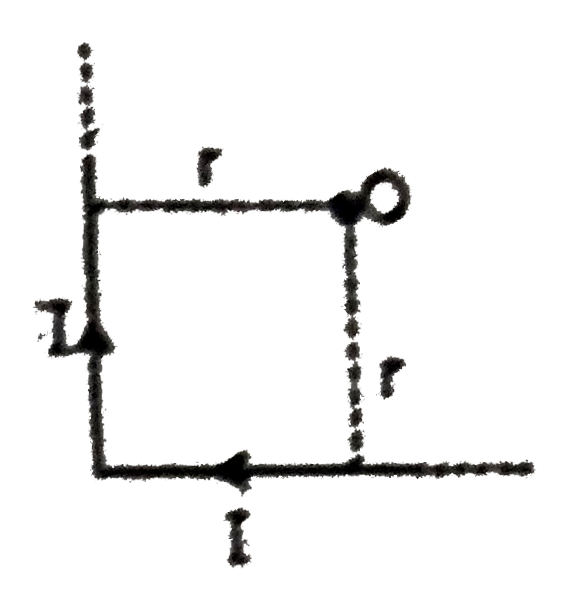
zero
μ0I/2πr
μ0I2πr(1+1√2)
μ0I4πr(1+1√2)
The correct Answer is:C
B=2μ04πr[sin45∘+sin90∘)=μ0I2πr(1+1√2)
Topper's Solved these Questions
Similar Questions
A long wire carrying current 'I' is bent into the shape as shown in the figure. The net magnetic field intensity at the centre 'O' is

View SolutionA current carrying wire AB of the length L is turned along a circle, as shown in figure. The magnetic field at the centre O.

View SolutionTwo wires AO and OC carry equal currents i as shown in Fig. One end of both the wires extends to infinity. Angle AOC is α. The magnitude of magnetic field is point P on the bisector of these two wires at a distance r from point O is

View SolutionA long current carrying wire is bent as shown. The magnetic field induction at O is

View SolutionA long wire bent as shown in fig. carries current I. If the radius of the semicircular portion is a, the magnetic field at centre C is

View SolutionA current - carrying wire of certain length is bent to form an arc that substends an angle θ at the centre. Let B be the magnetic field at the centre due to this wire. The correct graph between B and θ is
View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is

View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is :

View SolutionThe wire loop shown in figure carries a current as shown. The magnetic field at the centre O is ,

View SolutionDetermine the magnetic field at the centre of the current carrying wire arrangement shown in Fig. The arrangement extends to infinity. (The wires joining the successive squares are along the line passing through the centre).
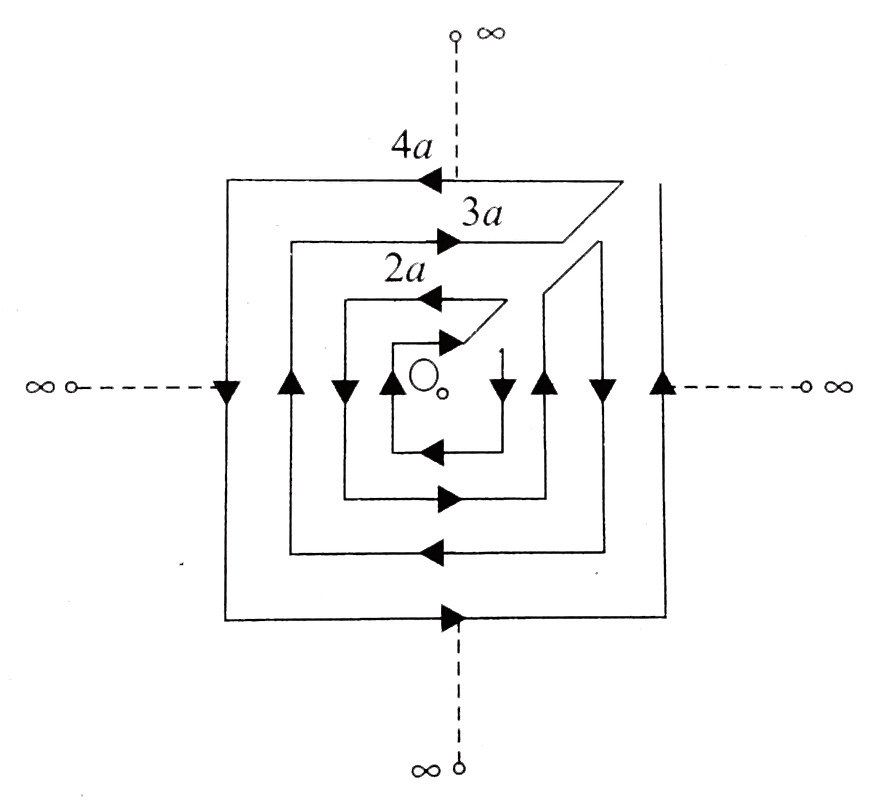
View Solution

