A current i is flowing in a straight conductor of length L. The magnetic induction at a point distant L4 from its centre will be-
4μ0i√5πL
μ0i2πL
μ0i√2L
zero
The correct Answer is:A
To find the magnetic induction (magnetic field) at a point located at a distance L4 from the center of a straight conductor of length L carrying a current I, we can follow these steps:
Step 1: Understanding the Geometry
We have a straight conductor of length L, and we want to find the magnetic field at a point P which is L4 away from the center of the conductor. The distance from the ends of the conductor to point P is L2 (half the length of the conductor) on one side and L4 on the other side.
Step 2: Use the Biot-Savart Law
The magnetic field B at a point due to a current-carrying conductor can be calculated using the Biot-Savart Law:
B=μ0I4πrsinθ
where r is the distance from the current element to the point where the field is being calculated, and θ is the angle between the current element and the line connecting the current element to the point.
Step 3: Calculate the Angles
For the point P:
- The distance from the center of the conductor to point P is L4.
- The distances from the ends of the conductor to point P are L2 and L4.
Using the geometry of the situation, we can find:
- sinθ1=L2√(L2)2+(L4)2
- sinθ2=sinθ1 (due to symmetry)
Calculating sinθ1:
sinθ1=L2√(L2)2+(L4)2=L2√L24+L216=L2√4L2+L216=L2√5L216=L2⋅4L√5=2√5
Step 4: Substitute into the Biot-Savart Law
Now substituting r=L4 and sinθ1=sinθ2=2√5 into the Biot-Savart Law:
B=μ0I4π(L4)(sinθ1+sinθ2)=μ0I4π(L4)(2⋅2√5)
B=μ0IπL⋅4√5
Step 5: Final Result
Thus, the magnetic induction at the point P is:
B=4μ0IπL√5
Conclusion
The magnetic induction at a point L4 from the center of the conductor is given by:
B=4μ0IπL√5
We have a straight conductor of length L, and we want to find the magnetic field at a point P which is L4 away from the center of the conductor. The distance from the ends of the conductor to point P is L2 (half the length of the conductor) on one side and L4 on the other side.
The magnetic field B at a point due to a current-carrying conductor can be calculated using the Biot-Savart Law:
B=μ0I4πrsinθ
where r is the distance from the current element to the point where the field is being calculated, and θ is the angle between the current element and the line connecting the current element to the point.
For the point P:
- The distance from the center of the conductor to point P is L4.
- The distances from the ends of the conductor to point P are L2 and L4.
- sinθ1=L2√(L2)2+(L4)2
- sinθ2=sinθ1 (due to symmetry)
sinθ1=L2√(L2)2+(L4)2=L2√L24+L216=L2√4L2+L216=L2√5L216=L2⋅4L√5=2√5
Now substituting r=L4 and sinθ1=sinθ2=2√5 into the Biot-Savart Law:
B=μ0I4π(L4)(sinθ1+sinθ2)=μ0I4π(L4)(2⋅2√5)
B=μ0IπL⋅4√5
Thus, the magnetic induction at the point P is:
B=4μ0IπL√5
The magnetic induction at a point L4 from the center of the conductor is given by:
B=4μ0IπL√5
Topper's Solved these Questions
Similar Questions
A current of 1A is flowing through a straight conductor of length 16cm. The magnetic induction ( in tesla ) at a point 10cm from the either end the wire is :
View SolutionA current I is flowing in a conductor of length L when it is bent in the form of a circular loop its magnetic moment
View SolutionCurrent 'i' is flowing in heaxagonal coil of side a. The magnetic induction at the centre of the coil will be
View SolutionA current I flows in the network shown in a adjacent figure. Resulting magnetic induction at point P is
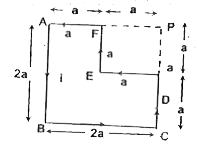
View SolutionA current of 1/(4π) ampere is flowing in a long straight conductor. The line integral of magnetic induction around a closed path enclosing the current carrying conductor is
View SolutionA current l is flowing through a long straight solid conductor of radius R = 4 cm. Magnetic field at a distance 2 cm from the axis of conductor is B0 The distance from the axis, where magnetic field is 1.5 B0 is (current density is uniform)
View SolutionCurrent I A flowing in a circular coil of radius r. then the magnetic induction at the centre is B. If the current is doubled then the magnetic induction will be
View SolutionA current I ampere flows along an infinitely long straight thin walled tube, then the magnetic induction at any point inside the tube is .
View SolutionA current i ampere flows along the inner conductor of a coaxial cable and returns along the outer conductor fo the cable, then the magnetic induction at any point outside the conductor at a distance r metre from the axis is
View SolutionA current flows in a conductor from east to west. The direction of the magnetic field at a points above the conductor is
View Solution

