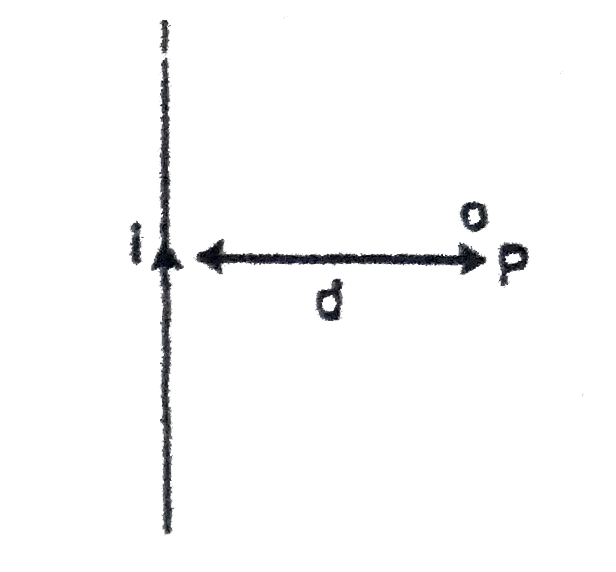
The magnetic flux density at a point distant d from a long straight current carrying conductor is B, then its value at distance d2 will be-
4B
2B
B2
B4
The correct Answer is:B
BP=μ0i2πd
B=μ0i2π(d/2)'(dtx=d2)
⇒B(d/2)=2B
Related Playlists
Similar Questions
The magnetic field in a straight current carrying conductor wire is:
View SolutionThe strength of the magnetic field at a point r near a long straight current carrying wire is B. The field at a distance r2 will be
View SolutionThe strength of the magnetic field at a point r near a long straight current carrying wire is B. The field at a distance r2 will be
View SolutionUsing Ampere.s circuital law, obtain an expression for the magnetic flux density .B. at a point .X. at a perpendicular distance .r. from a long current carrying conductor. (Statement of the law is not required).
View SolutionUsing Ampere 's circuital law or Biot- Savart's a law, show that magnetic flux density B at point P at a perpendicular distance a from a long current carrying conductor is given by B=(μ4π)2Ia [ Statement of the laws not required]
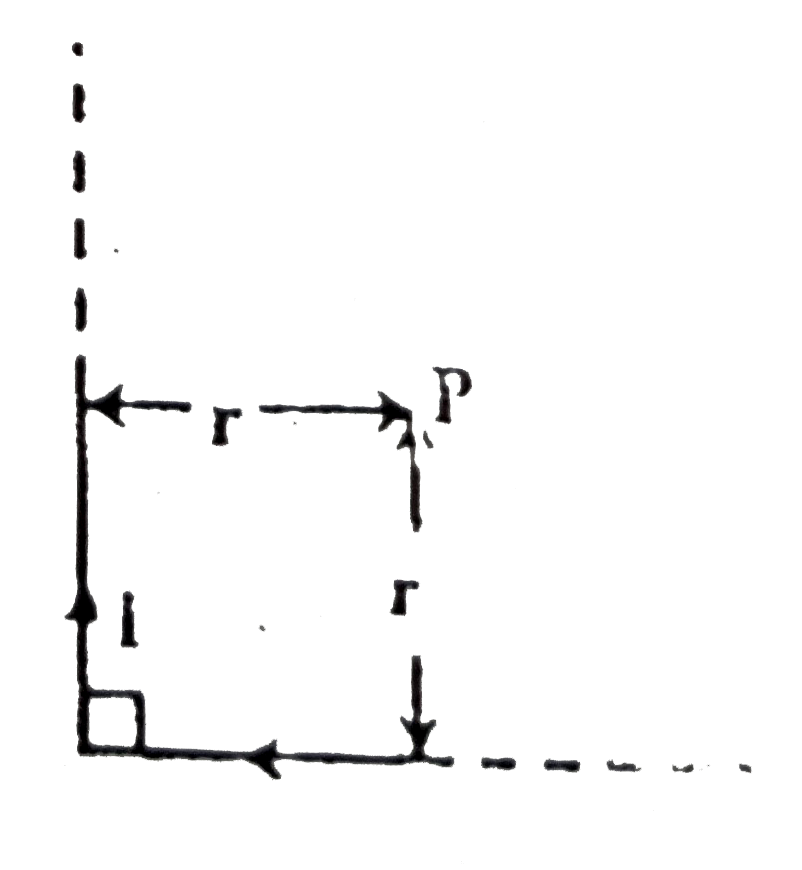
View SolutionThe magnetic field strength at a point P distant r due to an infinite straight wire carrying a current i is as shown in the figure
 View Solution
View Solution(a) Using Ampere.s circuital law or Biot Savart.s law, show that magnetic flux density .B. at a point P at a perpendicular distance.d from a long current carrying conductor is given by: B=(μ04π)2Ia (Statement of the law is not required)
(b) Define the terms (i) drift velocity, (ii) relaxation time. A conductor of length L is connected to a d.c. source of emf E. If this conductor is replaced by another conductor of same material and same area of cross-section but of length 3L, how will the drift velocity change?View SolutionMagnetic induction at a point due to a small element of current carrying conductor is
View SolutionMagnetic field at a distance a from long current carrying wire is proportional to
View SolutionFind magnetic flux density at a point on the axis of a long solenoid having 5000 turns/m when it carrying a current of 2 A
View Solution


