Question

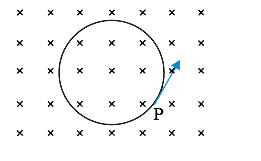
A particle having a charge$20\mu C$ and mass $20\mu g$ moves along a circle of radius 5.0 cm under the action of a magnetic field 5.0 cm under the action of a magnetic field B = 1.0 T. When the particle is at a point P, a uniform electric field is switched on and it is found that the particla continues on the tangent through P qith a uniform velocity. Find the electric field.

Options

A. 0.1 V/m
B. 0.5 V/m
C. 10.0 V/m
D. 100 V/m

Answer

B

Explanation

To solve the problem step by step, we will follow the principles of motion in magnetic and electric fields.

Step 1: Identify the given values
- Charge of the particle, \( Q = 20 \, \mu C = 20 \times 10^{-6} \, C \)
- Mass of the particle, \( m = 20 \, \mu g = 20 \times 10^{-9} \, kg \)
- Radius of the circular path, \( R = 5.0 \, cm = 5.0 \times 10^{-2} \, m \)
- Magnetic field strength, \( B = 1.0 \, T \)

Step 2: Use the formula for the radius of circular motion in a magnetic field
The radius \( R \) of the circular path of a charged particle moving in a magnetic field is given by the formula:
\( R = \frac{mv}{BQ} \)
Where:
- \( v \) is the velocity of the particle.

Step 3: Rearrange the formula to find the velocity
Rearranging the formula to solve for \( v \):
\( v = \frac{R \cdot B \cdot Q}{m} \)

Step 4: Substitute the known values into the equation
Substituting the values we have:
\( v = \frac{(5.0 \times 10^{-2}) \cdot (1.0) \cdot (20 \times 10^{-6})}{20 \times 10^{-9}} \)

Step 5: Calculate the velocity
Calculating the above expression:
\( v = \frac{(5.0 \times 10^{-2}) \cdot (1.0) \cdot (20 \times 10^{-6})}{20 \times 10^{-9}} = \frac{(5.0 \times 20) \times 10^{-8}}{20 \times 10^{-9}} = \frac{100 \times 10^{-8}}{20 \times 10^{-9}} = \frac{100}{20} \times 10^{1} = 5.0 \, m/s \)

Step 6: Find the electric field \( E \)
When the electric field is switched on, the particle continues to move with uniform velocity along the tangent. This means the electric force must balance the magnetic force acting on the particle.

The magnetic force \( F_B \) is given by:
\( F_B = QvB \)

The electric force \( F_E \) is given by:
\( F_E = QE \)

Since these forces are equal when the particle moves with uniform velocity:
\( QE = QvB \)

Step 7: Solve for the electric field \( E \)
Cancelling \( Q \) from both sides (since \( Q \neq 0 \)):
\( E = vB \)

Step 8: Substitute the values to find \( E \)
Substituting the values we calculated:
\( E = (5.0) \cdot (1.0) = 5.0 \, V/m \)

Step 9: Final result
Thus, the electric field \( E \) is:
\( E = 5.0 \, V/m \)