In the motorcycle stunt called " the well of death" the track is vertical cylindrical surface of 18 m radius.take the motorcyle to be a point mass and μ=0.8. The minimum angular speed of the motorcycle to prevent him from sliding down should be
6/5 rad/s
5/8 rad/s
25/3 rad/s
none of these
The correct Answer is:B
To solve the problem of determining the minimum angular speed of the motorcycle in the "well of death" stunt, we can follow these steps:
1. Identify the Forces Acting on the Motorcycle:
- The motorcycle experiences gravitational force (weight) acting downwards, which is mg.
- There is a normal force N acting perpendicular to the surface of the cylinder.
- There is a frictional force Ff acting upwards along the surface, which prevents the motorcycle from sliding down.
2. Relate the Forces:
- The frictional force can be expressed as:
Ff=μN
- The gravitational force acting on the motorcycle is:
Fg=mg
3. Centripetal Force Requirement:
- For the motorcycle to maintain circular motion, the net force acting towards the center of the circular path must equal the centripetal force required. The centripetal force is given by:
Fc=mω2r
- Here, r is the radius of the cylinder and ω is the angular speed.
4. Set Up the Equation:
- At the point of sliding, the frictional force must balance the gravitational force:
Ff=Fg
- Thus, we can write:
μN=mg
5. Substituting Normal Force:
- The normal force N can be expressed in terms of centripetal force:
N=mω2r
- Substituting this into the equation for friction gives:
μ(mω2r)=mg
6. Canceling Mass:
- Since m appears on both sides, we can cancel it out (assuming m≠0):
μω2r=g
7. Solving for Angular Speed ω:
- Rearranging the equation gives:
ω2=gμr
- Taking the square root:
ω=√gμr
8. Substituting the Values:
- Given:
- g=10m/s2
- μ=0.8
- r=18m
- Substitute these values into the equation:
ω=√100.8×18
9. Calculating:
- First calculate the denominator:
0.8×18=14.4
- Now calculate:
ω=√1014.4≈√0.6944≈0.833radians/second
10. Final Answer:
- The minimum angular speed of the motorcycle to prevent sliding down is approximately:
ω≈0.833radians/second
- The motorcycle experiences gravitational force (weight) acting downwards, which is mg.
- There is a normal force N acting perpendicular to the surface of the cylinder.
- There is a frictional force Ff acting upwards along the surface, which prevents the motorcycle from sliding down.
- The frictional force can be expressed as:
Ff=μN
- The gravitational force acting on the motorcycle is:
Fg=mg
- For the motorcycle to maintain circular motion, the net force acting towards the center of the circular path must equal the centripetal force required. The centripetal force is given by:
Fc=mω2r
- Here, r is the radius of the cylinder and ω is the angular speed.
- At the point of sliding, the frictional force must balance the gravitational force:
Ff=Fg
- Thus, we can write:
μN=mg
- The normal force N can be expressed in terms of centripetal force:
N=mω2r
- Substituting this into the equation for friction gives:
μ(mω2r)=mg
- Since m appears on both sides, we can cancel it out (assuming m≠0):
μω2r=g
- Rearranging the equation gives:
ω2=gμr
- Taking the square root:
ω=√gμr
- Given:
- g=10m/s2
- μ=0.8
- r=18m
- Substitute these values into the equation:
ω=√100.8×18
- First calculate the denominator:
0.8×18=14.4
- Now calculate:
ω=√1014.4≈√0.6944≈0.833radians/second
- The minimum angular speed of the motorcycle to prevent sliding down is approximately:
ω≈0.833radians/second
Topper's Solved these Questions
Similar Questions
A person wants to drive on the vertical surface of a large cylindrical wooden 'well' commonly known as 'death well' in a circus. The radius of the well is R and the coefficient of friction between the tyres of the motorcycle and the wall of the well is u. The minimum speed the motor cyclist must have in order to prevent slipping should be -
View SolutionA person wants to drive on the vertical suirface of a large cylindrical wooden well commonly known as deathwell in a circus. The radius of the well 2 meter, and the coefficient of friction between the tyers of the motorcycle and the wall of the well is 0.2 the minimum speed the motorcyclist must have in order to prevent slipping should be
View SolutionAn inclined plane of angule a is fixed onto a horizontal turntable with its line of greater slope in same plane as a diameter of forntable .A small block is placed on the inclined plane a distance r from the axis the coefficient of fraction between the block and the inclined plane is μ The turntable along with incline plane spins about its axis with constant minimum angular velocity ω
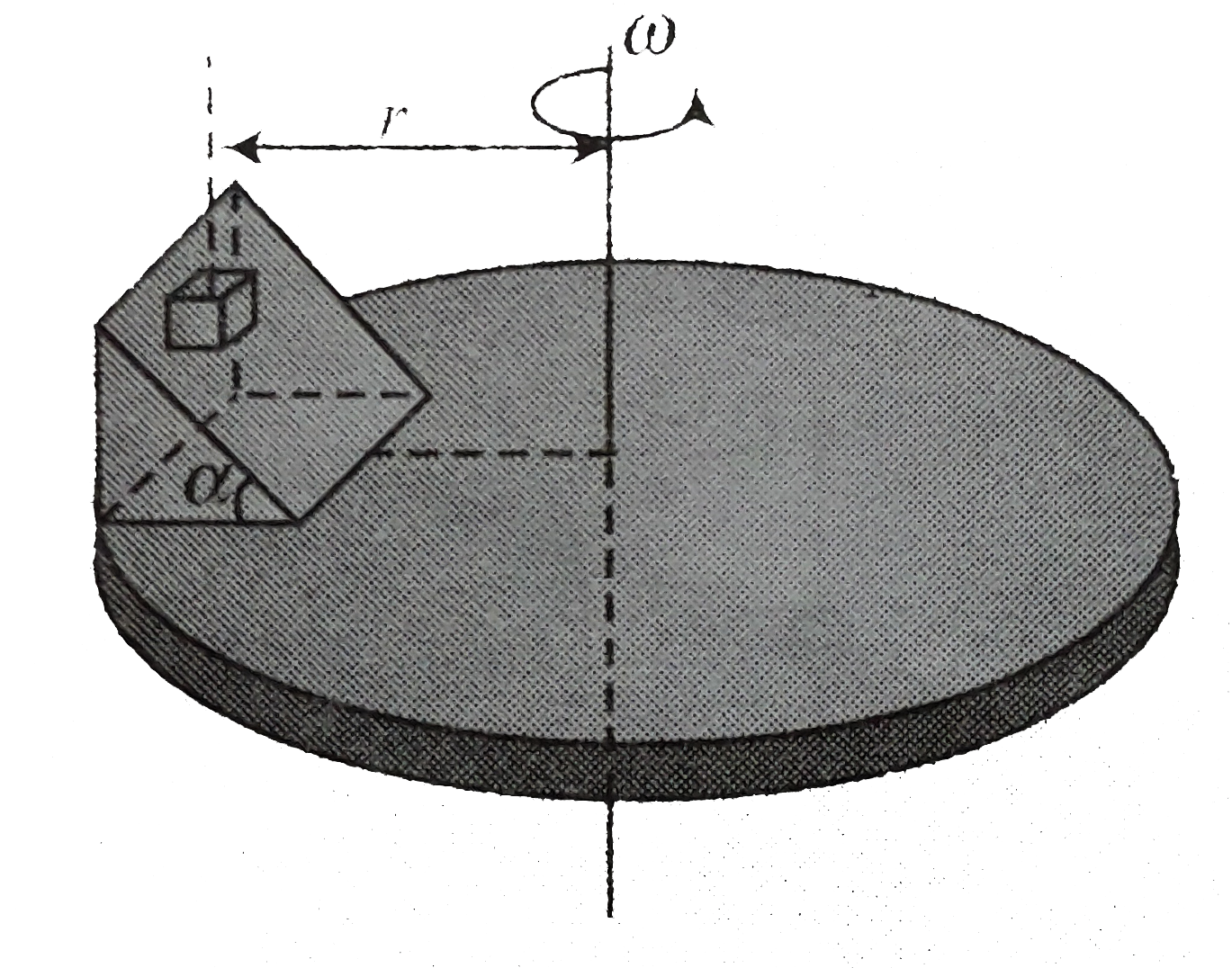
a. Find an capression for the minimum angular velocity ω to prevent the block from sliding down the plane in term of g,r,μ and the plane ω
b. Now a block of mass but having coefficient friction (with inclined plane)2μ is kept instead of the original block . find the radius of friction force acting between block and incline now to the friction force active in part (a)
View SolutionA block of mass 10 kg in contact against the inner wall of a hollow cylindrical drum of radius 1m. The coefficient of friction between the block and the inner wall of the cylinder is 0.1. The minimum angular velocity needed for the cylinder to keep the block stationary when the cylinder is vertical and rotating about its axis, will be (g=10m/s2)
View SolutionA small bead of mass m = 1 kg is free to move on a circular hoop. The circular hoop has centre at C and radius r = 1 m and it rotates about a fixed vertical axis. The coefficient of friction between bead and hoop is μ=0.5. The maximum angular speed of the hoop for which the bead does not have relative motion with respect to hoop, at the position shown in figure is : (Take g=10m/s2)
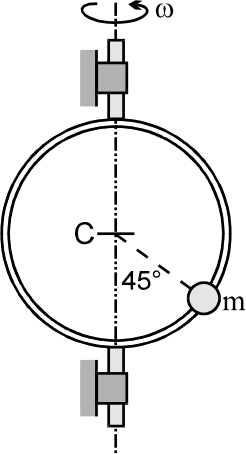
View SolutionTwo blocks of mass m1=10kg and m2=5kg connected to each other by a massless inextensible string of length 0.3m are placed along a diameter of the turntable. The coefficient of friction between the table and m1 is 0.5 while there is no friction between m2 and the table. the table is rotating with an angular velocity of 10rad/s. about a vertical axis passing through its center O. the masses are placed along the diameter of the table on either side of the center O such that the mass m1 is at a distance of 0.124m from O. the masses are observed to be at a rest with respect to an observed on the tuntable (g=9.8m/s2).
(a) Calculate the friction on m1
(b) What should be the minimum angular speed of the turntable so that the masses will slip from this position?
(c ) How should the masses be placed with the string remaining taut so that there is no friction on m1.
View SolutionIn a rotor, a hollow vertical cylindrical structure rotates about its axis and a person rests against the inner wall. At a particular speed of the rotor, the floor below the person is removed and the person hangs resting against the wall without any floor. If the radius of the rotor is 2m and the coefficient of static friction between the wall and the person is 0.2, find the minimum speed at which the floor may be removed Take g=10ms2.
View SolutionShows two long metal rails placed horizontally and parallel to each other at a separation i. A uniform magnetic field b exists in the vertically downward direction. A wire of mass m can slide on the rails. The rails are connected to a constant current source which drives a current I in the circuirt. The friction coefficient between the rails and the wire is μ. (a) What should be the minimum value of μ which can prevent the wire from sliding on the rails? (b) Describe the motion of the wire if the value of μ is half the value found in the previous part.

View SolutionThe small particle of mass m is given an initial high velocity in the horizontal plane and winds its cord around the fixed vertical shaft of radius 1m. All motion occurs essentially in the horizontal plane. If the angular velocity of the cord is 0.8 rad/s when the distance from the particle to the tangency point is 5m, determine the angular velocity ω (in rad//s) of the cord after it has turned through an angle 1 rad.
View SolutionA long cylindrical tank of cross-sectional area 0.5m2 is filled with water. It has a small hole at a height 50cm from the bottom. A movable piston of cross-sectional area almost equal to 0.5m2 is fitted on the top of the tank such that it can slide in the tank freely. A load of 20kg is applied on the top of the water by piston, as shown in the figure. Calculate the speed of the water jet with which it hits the surface when piston is 1m above the bottom. (Ignore the mass of the piston)

View Solution