Question

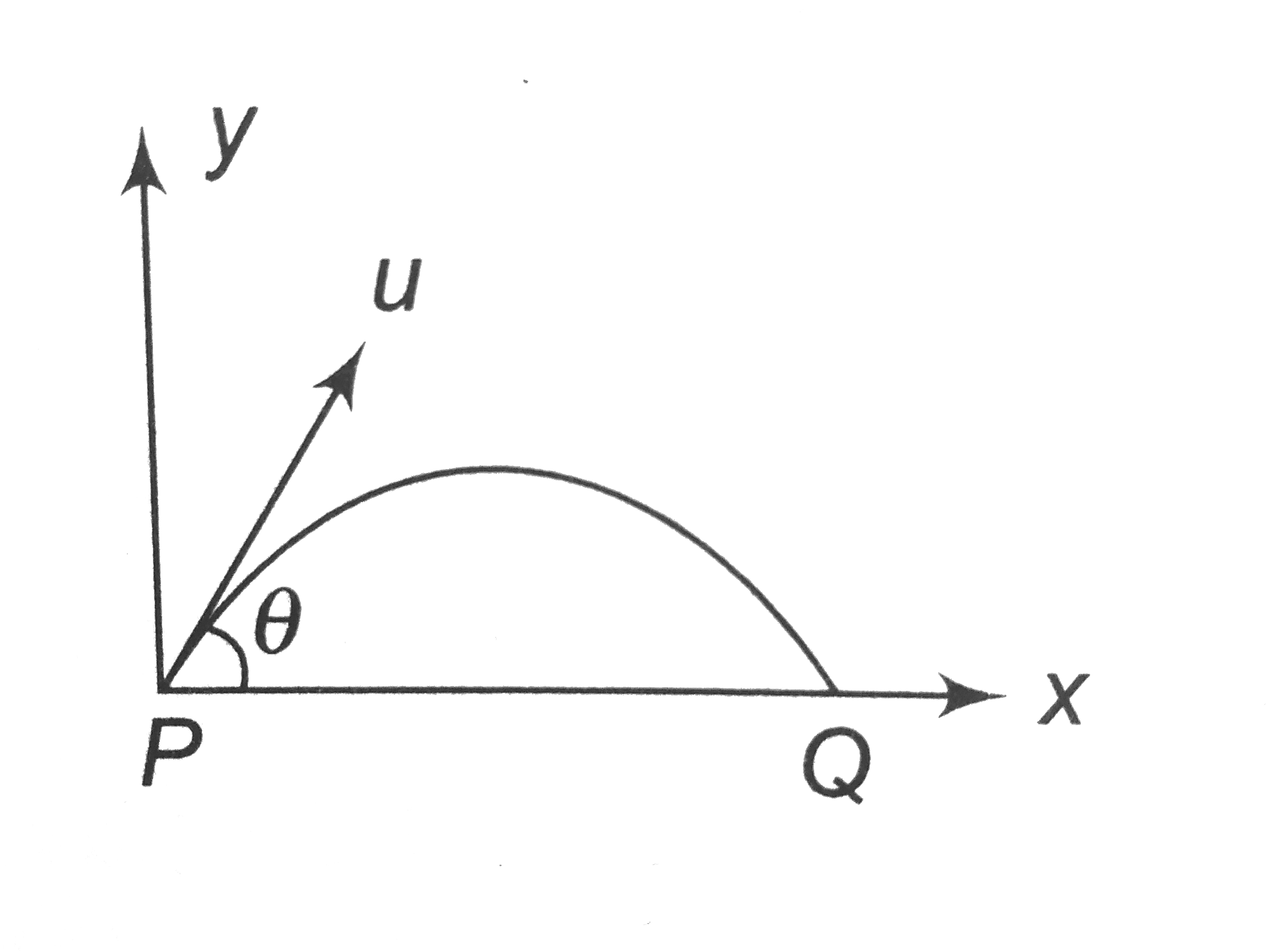
A stone is projected with speed u and angle of projection is $\theta$. Find radius of curvature at t=0.

Options

A. `(u^(2) cos^(2) theta)/g`
B. `(u^(2))/(g sin theta)`
C. `(u^(2))/(g cos theta)`
D. `(u^(2) sin^(2) theta)/g`

Answer

C

Explanation

To find the radius of curvature at $$t=0$$ for a stone projected with speed $$u$$ at an angle $$\theta$$, we can follow these steps:

Step 1: Identify the components of the initial velocity
When the stone is projected, its initial velocity \( u \) can be resolved into two components:
- Horizontal component: \( u_x = u \cos \theta \)
- Vertical component: \( u_y = u \sin \theta \)

Step 2: Determine the acceleration acting on the stone
The only acceleration acting on the stone after it is projected is the acceleration due to gravity, which acts downward. This acceleration can be denoted as:
- \( g \) (downward)

Step 3: Understand the concept of radius of curvature
The radius of curvature \( R \) at any point in a projectile motion can be calculated using the formula for centripetal acceleration:
\( a_c = \frac{v^2}{R} \)
Where:
- \( a_c \) is the centripetal acceleration,
- \( v \) is the tangential velocity at that point,
- \( R \) is the radius of curvature.

Step 4: Calculate the centripetal acceleration at \( t = 0 \)
At \( t = 0 \), the velocity of the stone is the initial velocity \( u \). The centripetal acceleration can be expressed as the component of gravitational acceleration that acts perpendicular to the velocity. The component of gravitational acceleration acting perpendicular to the velocity is given by:
\( a_c = g \cos \theta \)

Step 5: Substitute values into the radius of curvature formula
Now, substituting the values into the centripetal acceleration formula:
\( g \cos \theta = \frac{u^2}{R} \)
Rearranging this equation to solve for \( R \):
\( R = \frac{u^2}{g \cos \theta} \)

Conclusion
Thus, the radius of curvature at \( t = 0 \) is given by:
\( R = \frac{u^2}{g \cos \theta} \)