In a rotor, a hollow vertical cylindrical structure rotates about its axis and a person rests against the inner wall. At a particular speed of the rotor, the floor below the person is removed and the person hangs resting against the wall without any floor. If the radius of the rotor is 2m and the coefficient of static friction between the wall and the person is 0.2, find the minimum speed at which the floor may be removed Take g=10ms2.
To solve the problem, we need to find the minimum speed at which the floor can be removed from the rotor without causing the person to fall. We will use the concepts of circular motion and friction.
1. Identify the Forces Acting on the Person:
- The person experiences two main forces:
- The gravitational force (weight) acting downwards, Fg=mg.
- The frictional force acting upwards, which prevents the person from falling.
2. Determine the Centripetal Force:
- For the person to move in a circular path, a centripetal force is required. This force is provided by the normal force N exerted by the wall of the rotor.
- The centripetal force can be expressed as:
N=mv2r
- Here, r is the radius of the rotor, which is given as r=2m.
3. Frictional Force:
- The maximum static frictional force that can act on the person is given by:
Ffriction=μN
- Where μ is the coefficient of static friction, given as μ=0.2.
4. Setting Up the Equation:
- For the person to not fall, the frictional force must balance the gravitational force:
Ffriction≥Fg
- Substituting the expressions for the forces, we get:
μN≥mg
- Substituting N=mv2r:
μ(mv2r)≥mg
5. Canceling Mass:
- Since m appears on both sides, we can cancel it out (assuming m≠0):
μv2r≥g
6. Rearranging the Equation:
- Now, rearranging the equation to find v2:
v2≥grμ
7. Substituting Known Values:
- We know:
- g=10m/s2
- r=2m
- μ=0.2
- Plugging in these values:
v2≥10×20.2=200.2=100
8. Finding Minimum Speed:
- Taking the square root of both sides:
v≥√100=10m/s
Final Answer:
The minimum speed at which the floor may be removed is v=10m/s.
- The person experiences two main forces:
- The gravitational force (weight) acting downwards, Fg=mg.
- The frictional force acting upwards, which prevents the person from falling.
- For the person to move in a circular path, a centripetal force is required. This force is provided by the normal force N exerted by the wall of the rotor.
- The centripetal force can be expressed as:
N=mv2r
- Here, r is the radius of the rotor, which is given as r=2m.
- The maximum static frictional force that can act on the person is given by:
Ffriction=μN
- Where μ is the coefficient of static friction, given as μ=0.2.
- For the person to not fall, the frictional force must balance the gravitational force:
Ffriction≥Fg
- Substituting the expressions for the forces, we get:
μN≥mg
- Substituting N=mv2r:
μ(mv2r)≥mg
- Since m appears on both sides, we can cancel it out (assuming m≠0):
μv2r≥g
- Now, rearranging the equation to find v2:
v2≥grμ
- We know:
- g=10m/s2
- r=2m
- μ=0.2
- Plugging in these values:
v2≥10×20.2=200.2=100
- Taking the square root of both sides:
v≥√100=10m/s
The minimum speed at which the floor may be removed is v=10m/s.
Topper's Solved these Questions
- CIRCULAR MOTIONBook:HC VERMA ENGLISHChapter:CIRCULAR MOTIONExercise:Objective -1
Explore 16 Videos
- CIRCULAR MOTIONBook:HC VERMA ENGLISHChapter:CIRCULAR MOTIONExercise:Objective -2
Explore 6 Videos
- CIRCULAR MOTIONBook:HC VERMA ENGLISHChapter:CIRCULAR MOTIONExercise:Question for short Answer
Explore 10 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBook:HC VERMA ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONExercise:Objective -2
Explore 11 Videos
- FLUID MECHANICSBook:HC VERMA ENGLISHChapter:FLUID MECHANICSExercise:All Questions
Explore 90 Videos
Similar Questions
IN a rotor, a hollow verticla cylindrical structure rotates about its axis and a person rests asgainst he inner wall. At a particular speed of the rotor, the floor below the person is removed and the person hangs resting against the wall without any floor. If the radius of the roter is 2m and the coefficient of static frictioin between the wall and theperson is 0.2, find the minimum speed at which the floor may be removed Take g=10ms2.
View SolutionA 70 kg man stands in contact against the inner wall of a hollow cylindrical drum of radius 3 m rotating about its vertical axis with 200 rev/min. The coefficient of friction between the wall and his clothing is 0.15 m What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed ?
View SolutionA body is pushed against vertical wall as shown. If the coefficient of friction between the body and the wall is 0.5, the magnitude of acceleration of the block is 10 K. Where K is
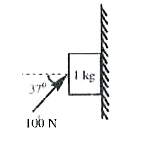
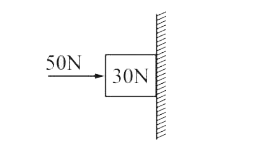
View SolutionA block of weight 30 N is in contact with a rough wall. A force of 50 N is applied as shown in the figure. Find the coefficient of static friction between the wall and the block assuming the block is just about to slip.
View SolutionA person stands in contact against the inner wall of a rotor of radius r. The coefficient of friction between the wall and the clothing is μ and the rotor is rotating about vertical axis. The minimum angular speed of the rotor so that the person does not slip downward is
View SolutionA block of weight 5 N is pushed against a vertical wall by a force 12 N . The coefficient of friction between the wall and block is 0.6 . Find the magnitude of the force exerted by the wall on the block :
View SolutionA block of mass 1 kg is pressed against a wall by applying a horizontal force of 10N on the block. If the coefficient of friction between the block and the wall is 0.5, magnitude of the frictional force acting on the block is
View SolutionA block of mass m kg is pushed up against a wall by a force P that makes an angle 'θ' with the horizontal as shown in figure. The coefficient of static friction between the block and the wall is μ. The minimum value of P that allows the block to remain stationary is
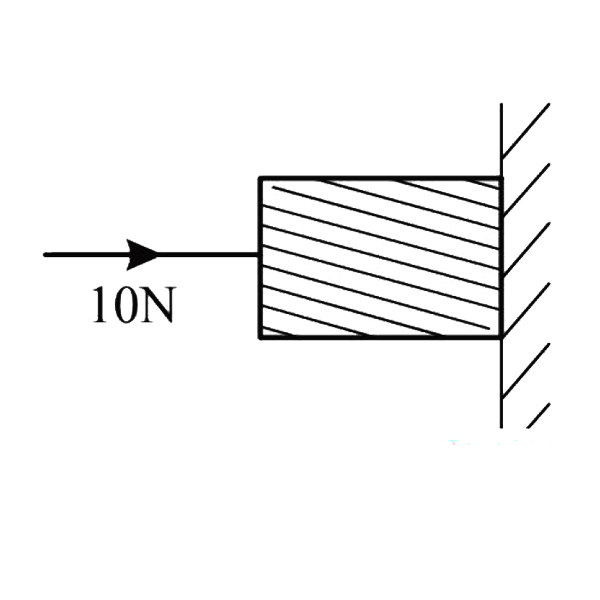
View SolutionA horizontal force of 10 N is necessary to just hold a block stationary against a wall. The coefficient of friction between the block and the wall is 0.2. the weight of the block is (g=10m/s2)

View SolutionA horizontal force of 10N is necessary to just hold a block stationary against as well. The coefficient of friction between the block and the wall is 0.2. The weight of the block is
View Solution

