Water is filled in a flask up to a height of 20 cm. The bottom of the flask is circular with radius 10 cm. If the atmospheric pressure is Pa, find the force exerted by the water on the bottom. Take and density of water =1000 kgm^-3.
To solve the problem, we need to find the force exerted by the water on the bottom of the flask. We will follow these steps:
Step 1: Calculate the pressure at the bottom of the flask
The pressure at the bottom of the flask can be calculated using the formula:
P=Patmospheric+ρgh
Where:
- Patmospheric=1.01×105Pa
- ρ=1000kg/m3 (density of water)
- g=10m/s2 (acceleration due to gravity)
- h=0.2m (height of water in meters, since 20 cm = 0.2 m)
Substituting the values:
P=1.01×105+(1000×10×0.2)
P=1.01×105+2000
P=1.01×105+2×103
P=1.03×105Pa
Step 2: Calculate the area of the bottom of the flask
The area A of the circular bottom of the flask can be calculated using the formula:
A=πr2
Where:
- r=0.1m (radius of the flask in meters, since 10 cm = 0.1 m)
Substituting the value:
A=π(0.1)2
A=π(0.01)
A≈0.0314m2 (using π≈3.14)
Step 3: Calculate the force exerted by the water on the bottom of the flask
The force F can be calculated using the formula:
F=P×A
Substituting the values:
F=(1.03×105)×(0.0314)
F≈3230.2N
Final Answer
The force exerted by the water on the bottom of the flask is approximately 3230 N.
---
The pressure at the bottom of the flask can be calculated using the formula:
P=Patmospheric+ρgh
- Patmospheric=1.01×105Pa
- ρ=1000kg/m3 (density of water)
- g=10m/s2 (acceleration due to gravity)
- h=0.2m (height of water in meters, since 20 cm = 0.2 m)
P=1.01×105+(1000×10×0.2)
P=1.01×105+2000
P=1.01×105+2×103
P=1.03×105Pa
The area A of the circular bottom of the flask can be calculated using the formula:
A=πr2
- r=0.1m (radius of the flask in meters, since 10 cm = 0.1 m)
A=π(0.1)2
A=π(0.01)
A≈0.0314m2 (using π≈3.14)
The force F can be calculated using the formula:
F=P×A
F=(1.03×105)×(0.0314)
F≈3230.2N
The force exerted by the water on the bottom of the flask is approximately 3230 N.
Topper's Solved these Questions
Similar Questions
Calculate the pressure due to a water column of height 100 m. (Take g=10ms−2 and density of water =103kgm−3).
View SolutionThe manometer has a water column difference of 50 cm . If the atmospheric pressure is 105 Pa, find the pressure of the gas in the container .
View SolutionA beaker of circular cross-section of radius 4 cm is filled with mercury up to a height of 10 cm. Find the force exerted by the mercury on the bottom of the beaker. The atmospheric pressure =105Nm−2. Density of mercury =13600kgm−3.Takeg10ms−2
View SolutionA water pump raises 50 litres of water through a height of 25 m in 5 .Calculate the power of the pump required . (Take g=10 N kg−1 and density of water =1000 kg m−3)
View SolutionWhat is the pressure in an ocean at a depth of 1000 m, if the density of water is 1.024×103kgm3. Atmospheric pressure P.=1.01×105 Pa.
View SolutionA curved glass vessel full of water upto a height of 10 cm has a bottom of area 10cm2, top of area 30cm2 and volume 1 L.
(i) Find the force exerted by the water on the bottom.
(ii) Find the resultant force exerted by the sides of the glass on the water.
(iii) If the glass vessel is covered by a jar and the air inside the jar is completely pumped out, what will be the answers to parts (a) and (b)
(iv) If a glass vessel of different shape is used provided the height, the bottom area and the volume are unchanged, will the answers to parts (a) and (b) change.
(Take, g=10ms−2 , density of water =103kgm−2 and atmospheric pressure =1.01×105Nm−2)
View SolutionA glass full of water upto a height of 10 cm has a bottom of are 10cm2, top of area 30cm2 and volume 1 litre.
(a) Find the force exerted by the water on the bottom.
(b) Find the resultant force exerted by the sides of the glass on the water.
(c ) If the glass is convered by a jar and the air inside the jar is completely pumped out, what will be the answer to parts (a) and (b).
(d) If a glass of different shape is used, provided the height, the bottom area, the top area and the volume are unchanged, will the answer to parts (a) and (b) change.
Take g=10m/s3, density of water=103kg/m3 and atmospheric pressure =1.01×105N/m2.
View SolutionWhat is the pressure on a swimmer 10m below the surface of lake? g=10ms−2, atmospheric pressure = 1.01×105Pa
View SolutionA tank of base area 4m2 is initially filled with water up to height 2m. An object of uniform cross-section 2m2 and height 1m is now suspended by wire into the tank, keeping distance between base of tank and that of object 1m. Density of the object is 2000kg/m3. Take atmospheric pressure 1×105N/m2,g=10m/s2.
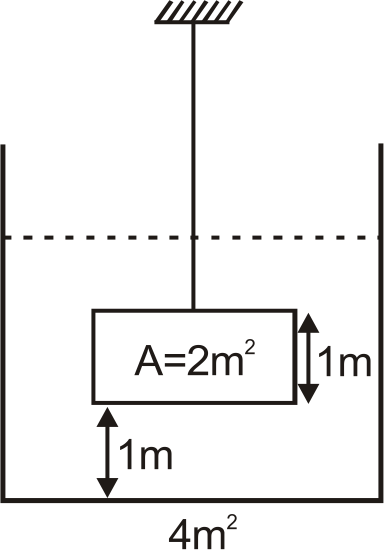
The downwards force exerted by the water on the top surface of the object is
View SolutionA glass full of water has a bottom of area 20cm2, top of area 20cm, height 20cm and volume half a litre.
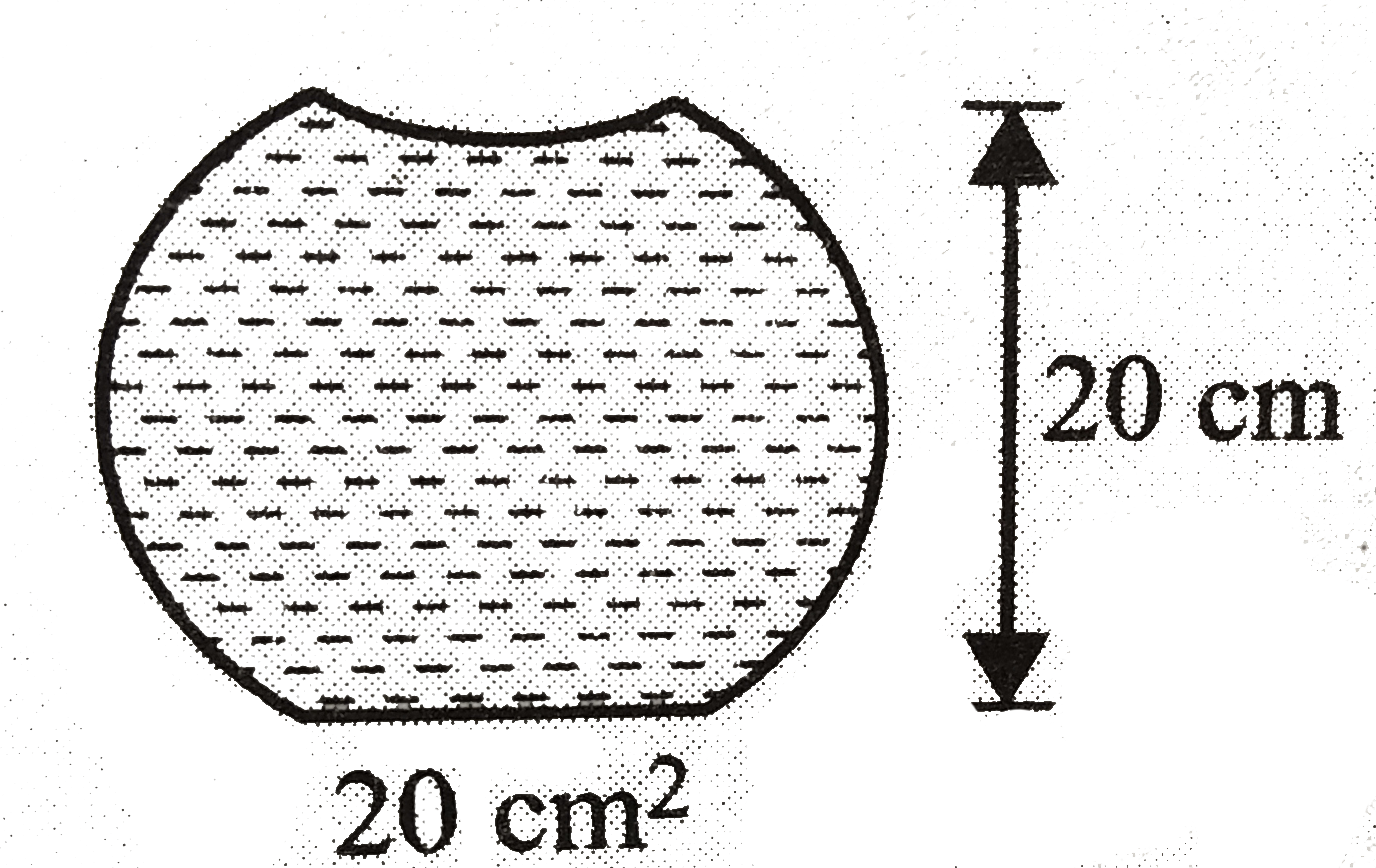
a. Find the force exerted by the water on the bottom.
b. Considering the equilibrium of the v, after. find the resultant force exerted by the side, of the glass on the water. Atmospheric pressure =1.0×105N/m2. Density of water =1000kg/m−3 and g=10m/s2
View Solution