A curved glass vessel full of water upto a height of 10 cm has a bottom of area 10cm2, top of area 30cm2 and volume 1 L.
(i) Find the force exerted by the water on the bottom.
(ii) Find the resultant force exerted by the sides of the glass on the water.
(iii) If the glass vessel is covered by a jar and the air inside the jar is completely pumped out, what will be the answers to parts (a) and (b)
(iv) If a glass vessel of different shape is used provided the height, the bottom area and the volume are unchanged, will the answers to parts (a) and (b) change.
(Take, g=10ms−2 , density of water =103kgm−2 and atmospheric pressure =1.01×105Nm−2)
To solve the problem step by step, we will address each part of the question sequentially.
Given Data:
- Height of water (h) = 10 cm = 0.1 m
- Area of the bottom (A_bottom) = 10 cm² = 10 / 10000 m² = 0.001 m²
- Area of the top (A_top) = 30 cm² = 30 / 10000 m² = 0.003 m²
- Volume of water (V) = 1 L = 0.001 m³
- Density of water (ρ) = 1000 kg/m³
- Acceleration due to gravity (g) = 10 m/s²
- Atmospheric pressure (P₀) = 1.01 × 10⁵ N/m²
(i) Find the force exerted by the water on the bottom.
1. Calculate the pressure at the bottom of the vessel:
P=P0+ρgh
Substituting the values:
P=1.01×105+(1000kg/m3)(10m/s2)(0.1m)
P=1.01×105+1000×10×0.1
P=1.01×105+1000
P=1.01×105+103=1.02×105N/m2
2. Calculate the force exerted on the bottom:
F=P×Abottom
F=(1.02×105)×(0.001)
F=102N
(ii) Find the resultant force exerted by the sides of the glass on the water.
1. Calculate the pressure at the top of the water:
Ptop=P0+ρgh
Since the height is the same, the pressure at the top is:
Ptop=1.01×105+1000×10×0.1=1.02×105N/m2
2. Calculate the force exerted by the water on the sides:
The force on the sides can be calculated using the average pressure over the height of the water. The average pressure is:
Pavg=Pbottom+Ptop2=1.02×105+1.01×1052=1.015×105N/m2
3. Calculate the area of the sides:
The lateral area of the curved surface can be approximated as:
Asides=perimeter×height
The perimeter of the top is:
Perimeter=2πr(assuming circular top)
However, we can also use the average area (A_top) for simplicity:
Asides=Atop×h=0.003m2×0.1m=0.0003m2
4. Calculate the resultant force on the sides:
Fsides=Pavg×Asides=1.015×105×0.0003
Fsides=30.45N
(iii) If the glass vessel is covered by a jar and the air inside the jar is completely pumped out, what will be the answers to parts (a) and (b)?
1. Force on the bottom:
The pressure at the bottom will now be:
P=ρgh=1000×10×0.1=1000N/m2
The force on the bottom will be:
F=P×Abottom=1000×0.001=1N
2. Resultant force on the sides:
Since there is no atmospheric pressure acting on the water, the force on the sides will also be:
Fsides=0N
(iv) If a glass vessel of different shape is used provided the height, the bottom area and the volume are unchanged, will the answers to parts (a) and (b) change?
- The force exerted on the bottom depends only on the height of the water column and the area of the bottom. As long as these values remain unchanged, the force on the bottom will remain the same.
- The resultant force on the sides will also remain the same because it depends on the average pressure acting over the height of the water, which is unchanged.
Summary of Answers:
(i) Force on the bottom = 102 N
(ii) Resultant force on the sides = 30.45 N
(iii) Force on the bottom = 1 N, Resultant force on the sides = 0 N
(iv) No change in answers for parts (a) and (b).
- Height of water (h) = 10 cm = 0.1 m
- Area of the bottom (A_bottom) = 10 cm² = 10 / 10000 m² = 0.001 m²
- Area of the top (A_top) = 30 cm² = 30 / 10000 m² = 0.003 m²
- Volume of water (V) = 1 L = 0.001 m³
- Density of water (ρ) = 1000 kg/m³
- Acceleration due to gravity (g) = 10 m/s²
- Atmospheric pressure (P₀) = 1.01 × 10⁵ N/m²
P=P0+ρgh
Substituting the values:
P=1.01×105+(1000kg/m3)(10m/s2)(0.1m)
P=1.01×105+1000×10×0.1
P=1.01×105+1000
P=1.01×105+103=1.02×105N/m2
F=P×Abottom
F=(1.02×105)×(0.001)
F=102N
Ptop=P0+ρgh
Since the height is the same, the pressure at the top is:
Ptop=1.01×105+1000×10×0.1=1.02×105N/m2
The force on the sides can be calculated using the average pressure over the height of the water. The average pressure is:
Pavg=Pbottom+Ptop2=1.02×105+1.01×1052=1.015×105N/m2
The lateral area of the curved surface can be approximated as:
Asides=perimeter×height
The perimeter of the top is:
Perimeter=2πr(assuming circular top)
However, we can also use the average area (A_top) for simplicity:
Asides=Atop×h=0.003m2×0.1m=0.0003m2
Fsides=Pavg×Asides=1.015×105×0.0003
Fsides=30.45N
The pressure at the bottom will now be:
P=ρgh=1000×10×0.1=1000N/m2
The force on the bottom will be:
F=P×Abottom=1000×0.001=1N
Since there is no atmospheric pressure acting on the water, the force on the sides will also be:
Fsides=0N
- The resultant force on the sides will also remain the same because it depends on the average pressure acting over the height of the water, which is unchanged.
(i) Force on the bottom = 102 N
(ii) Resultant force on the sides = 30.45 N
(iii) Force on the bottom = 1 N, Resultant force on the sides = 0 N
(iv) No change in answers for parts (a) and (b).
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Example 13.71videos
FLUID MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Example 13.81videos
FLUID MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Example 13.51videos
FLUID MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective15videos
EXPERIMENTS
- BOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE2videos
GENERAL PHYSICS
Similar Questions
A glass full of water upto a height of 10 cm has a bottom of are 10cm2, top of area 30cm2 and volume 1 litre.
(a) Find the force exerted by the water on the bottom.
(b) Find the resultant force exerted by the sides of the glass on the water.
(c ) If the glass is convered by a jar and the air inside the jar is completely pumped out, what will be the answer to parts (a) and (b).
(d) If a glass of different shape is used, provided the height, the bottom area, the top area and the volume are unchanged, will the answer to parts (a) and (b) change.
Take g=10m/s3, density of water=103kg/m3 and atmospheric pressure =1.01×105N/m2.View SolutionA glass full of water has a bottom of area 20cm2, top of area 20cm, height 20cm and volume half a litre.
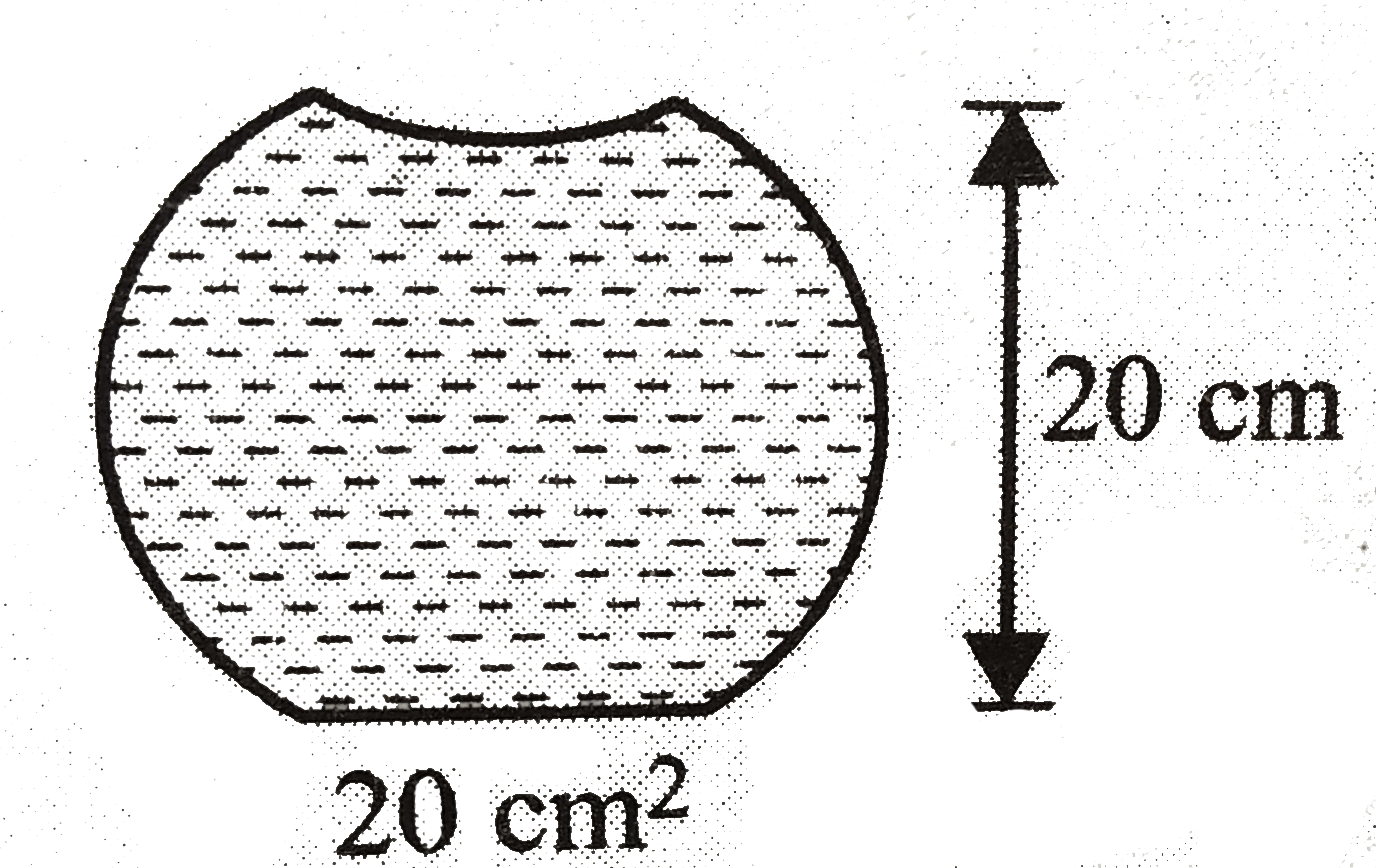
a. Find the force exerted by the water on the bottom.
b. Considering the equilibrium of the v, after. find the resultant force exerted by the side, of the glass on the water. Atmospheric pressure =1.0×105N/m2. Density of water =1000kg/m−3 and g=10m/s2View Solution
Knowledge Check
- Question 1 - Select One
Three vessels A,B,and C of different shapes contain a water upto the same height as shown in the figure .PA,PB ,and PC be the pressure exerted by the water at the bottom of the vessels A ,B and C respectively . Then
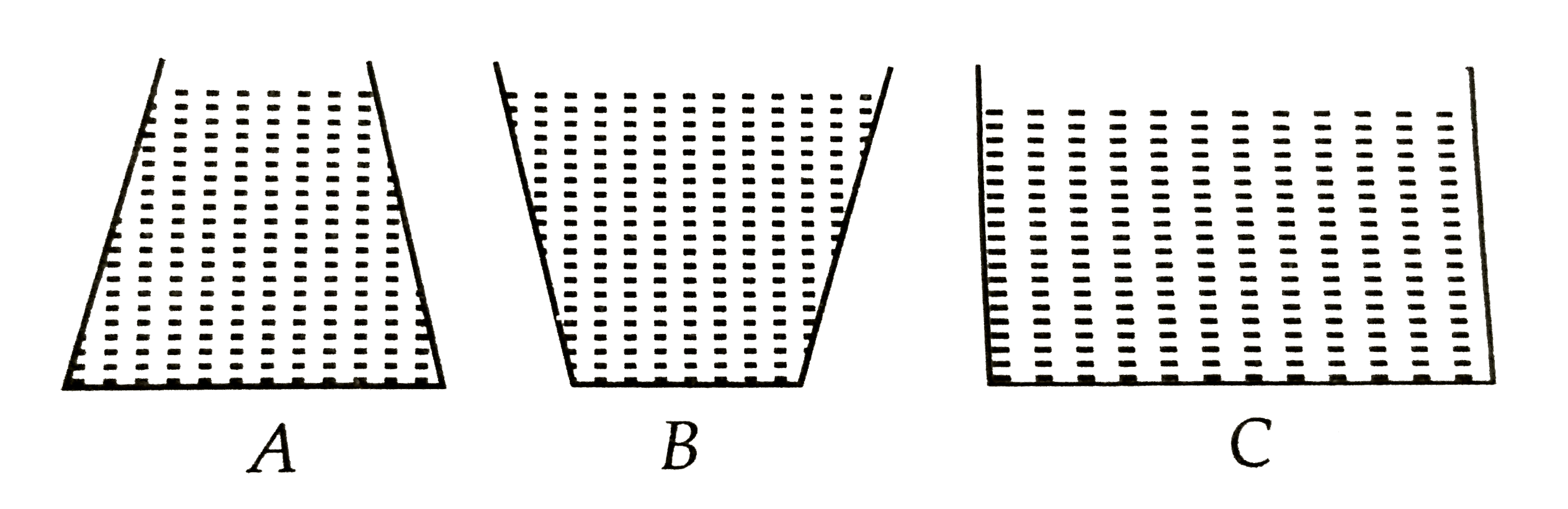 APA>PB>PCBPB>PC>PACPC>PB>PADPA=PB=PC
APA>PB>PCBPB>PC>PACPC>PB>PADPA=PB=PC
Water is filled in a flask up to a height of 20 cm. The bottom of the flask is circular with radius 10 cm. If the atmospheric pressure is 1.01×105 Pa, find the force exerted by the water on the bottom. Take g=10ms−2 and density of water =1000 kgm^-3.
View SolutionA piece of ice is floating in a glass vessel filled with water. Then prove that level of water in the vessel remains unchanged after melting of ice.
View SolutionThe neck and bottom of a bottle are 3 cm and 15 cm in radius respectively. If the cork is pressed with a force 12 N in the neck of the bottle, then force exerted on the bottom of the bottle is :-
View SolutionThe height of water in a vessel is h. The vessel wall of width b is at an angle θ to the vertical. The net force exerted by the water on the wall is
 View Solution
View SolutionA metal piece of mass 160 g lies iln equilibrium inside a glass of water figure. The ppece touches the bottom of the glass at a small number of points. If the density of the metl is 8000 kg m−3, find the normal fore exerted by the bottom of the glass on the metal piece.
 View Solution
View SolutionA piece of ice is floating in a glass vessel filled with water. How will the level of water in the vessel change when the ice melts ?
View SolutionA vessel in the form of a truncated cone has base area a1 and top area a2. It is filled to the brim with a liquid. The force at the bottom of the vessel is
View Solution
