A metal rign of mass m and radius R is placed on a smooth horizontal table and is set rotating abut its own axis in such a way that each part of the ring moves with a speed v. Find the tension in the ring.
To find the tension in a rotating metal ring of mass m and radius R where each part of the ring moves with speed v, we can follow these steps:
1. Understand the System:
- We have a metal ring of mass m and radius R rotating about its own axis. Each part of the ring moves with a speed v.
2. Consider a Small Segment of the Ring:
- Take a small segment of the ring that subtends an angle dθ at the center. The length of this small segment is given by:
Length=Rdθ
3. Identify Forces Acting on the Segment:
- The small segment experiences tension T acting towards the center of the ring on both sides.
4. Draw the Force Diagram:
- The tension forces can be represented as T acting at both ends of the segment. The angle between the two tension forces is 2×(90∘−dθ2)=180∘−dθ.
5. Calculate the Resultant Force:
- The resultant force due to the tension can be calculated using the sine of the angle between the two tension forces:
Fresultant=2Tsin(dθ2)
- For small angles, sin(dθ2)≈dθ2, so:
Fresultant≈2T⋅dθ2=Tdθ
6. Relate the Resultant Force to Centripetal Force:
- This resultant force acts as the centripetal force required to keep the small segment in circular motion. Therefore, we can set it equal to the centripetal force:
Tdθ=dm⋅v2R
7. Find the Mass of the Small Segment:
- The mass dm of the small segment can be expressed in terms of the mass per unit length λ:
dm=λ⋅Length=λ⋅Rdθ
- The mass per unit length λ is given by:
λ=m2πR
- Thus, substituting this into the equation gives:
dm=m2πR⋅Rdθ=m2πdθ
8. Substitute dm into the Force Equation:
- Now substitute dm back into the centripetal force equation:
Tdθ=m2πdθ⋅v2R
9. Solve for Tension T:
- Cancel dθ from both sides (assuming dθ≠0):
T=mv22πR
Final Answer:
The tension in the ring is given by:
T=mv22πR
- We have a metal ring of mass m and radius R rotating about its own axis. Each part of the ring moves with a speed v.
- Take a small segment of the ring that subtends an angle dθ at the center. The length of this small segment is given by:
Length=Rdθ
- The small segment experiences tension T acting towards the center of the ring on both sides.
- The tension forces can be represented as T acting at both ends of the segment. The angle between the two tension forces is 2×(90∘−dθ2)=180∘−dθ.
- The resultant force due to the tension can be calculated using the sine of the angle between the two tension forces:
Fresultant=2Tsin(dθ2)
- For small angles, sin(dθ2)≈dθ2, so:
Fresultant≈2T⋅dθ2=Tdθ
- This resultant force acts as the centripetal force required to keep the small segment in circular motion. Therefore, we can set it equal to the centripetal force:
Tdθ=dm⋅v2R
- The mass dm of the small segment can be expressed in terms of the mass per unit length λ:
dm=λ⋅Length=λ⋅Rdθ
- The mass per unit length λ is given by:
λ=m2πR
- Thus, substituting this into the equation gives:
dm=m2πR⋅Rdθ=m2πdθ
- Now substitute dm back into the centripetal force equation:
Tdθ=m2πdθ⋅v2R
- Cancel dθ from both sides (assuming dθ≠0):
T=mv22πR
The tension in the ring is given by:
T=mv22πR
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - HC VERMA ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Objective -1
16 Videos
- CIRCULAR MOTIONBOOK - HC VERMA ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Objective -2
6 Videos
- CIRCULAR MOTIONBOOK - HC VERMA ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Question for short Answer
10 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -2
11 Videos
- FLUID MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - All Questions
90 Videos
Similar Questions
A metal ring of mass m and radius R is placed on a smooth horizontal table and is set rotating about its own axis in such a way that each part of the ring moves with a speed v. Find the tension in the ring.
View SolutionFor a uniform ring of mass M and radius R at its centre
View SolutionA ring of mass m and radius R is placed on a rough inclined plane so that it rolls without slipping . Match the following table.


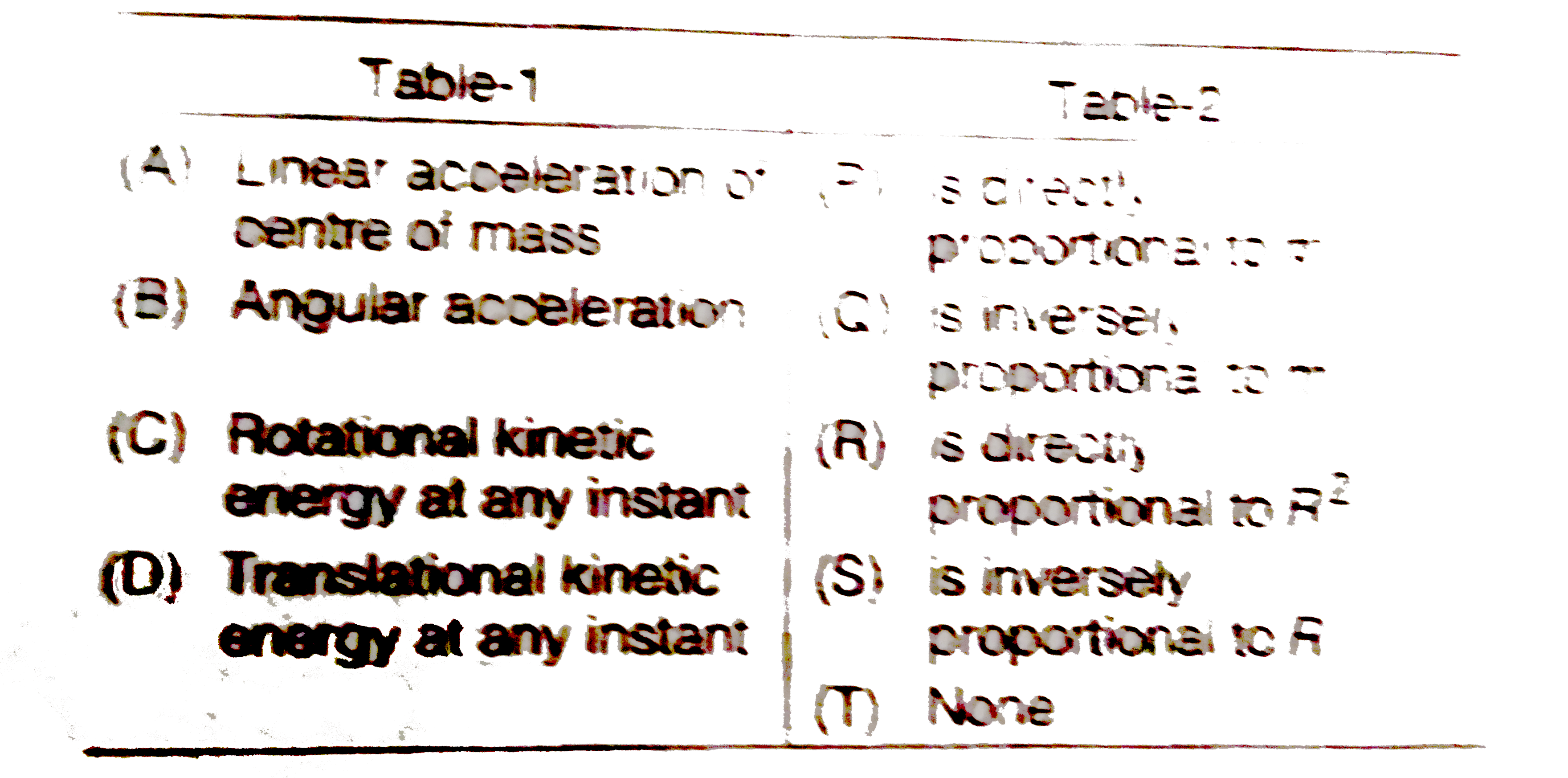
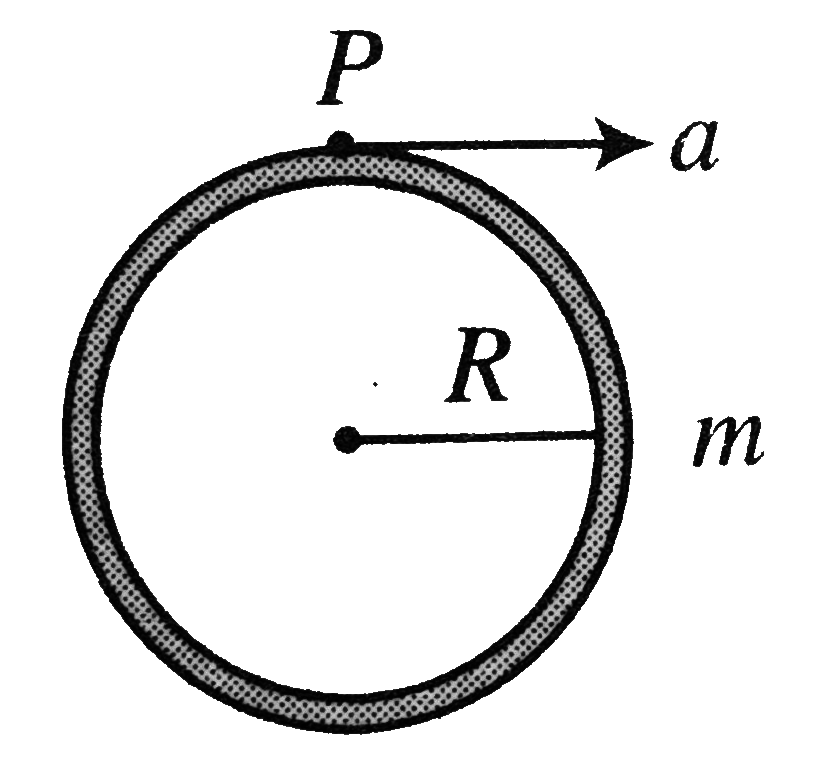
View SolutionA smooth ring of mass m and radius R=1m is pulled at P with a constant acceleration a=4ms−2 on a horizontal surface such that the plane of the ring lies on the surface. Find the angular acceleration of the ring at the given position. (in rad/s2)
View SolutionA ring of mass m and radius R is given a charge q. It is then rotated about its axis with angular velocity ω.Find
(iii)Magnetic moment of ring.
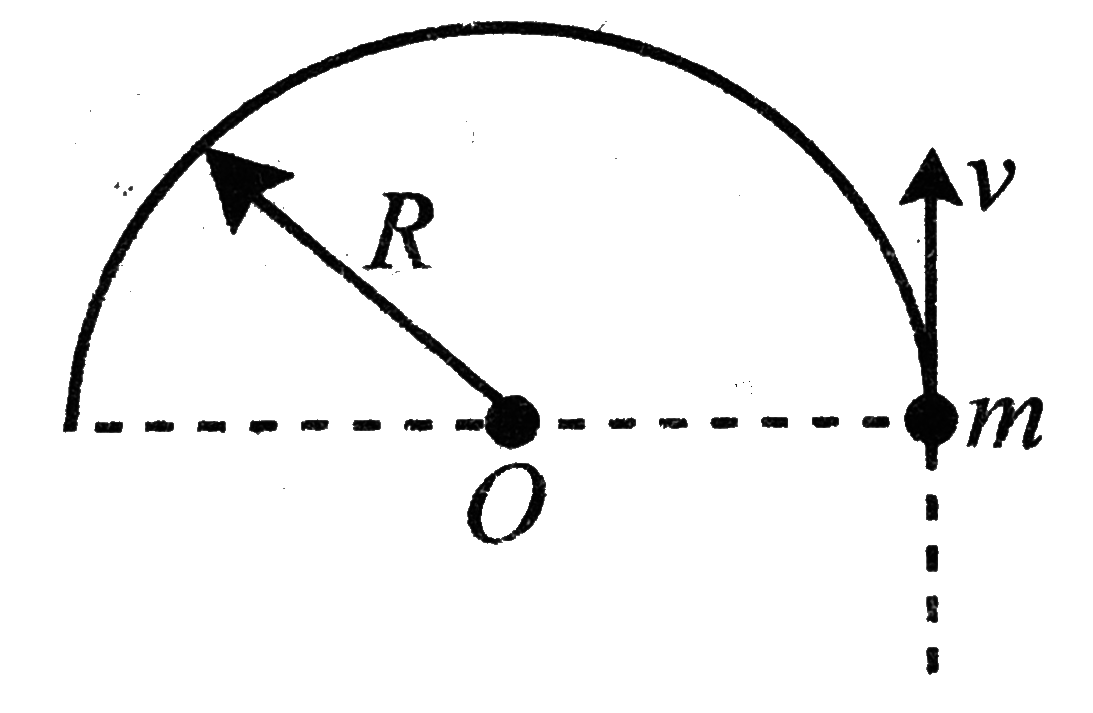
View SolutionA small bead of mass m moving with velocity v gets threaded on a stationary semicircular ring of mass m and radius R kept on a horizontal table. The ring can freely rotate about its centre. The bead comes to rest relative to the ring. What will be the final angular velocity of the system?
View SolutionFrom a complete ring of mass M and radius R, a 30∘sector is removed. The moment of inertia of the incomplete ring about an axis passing through the centre of the ring and perpendicular to the plane of the ring is
 ,
,
View Solution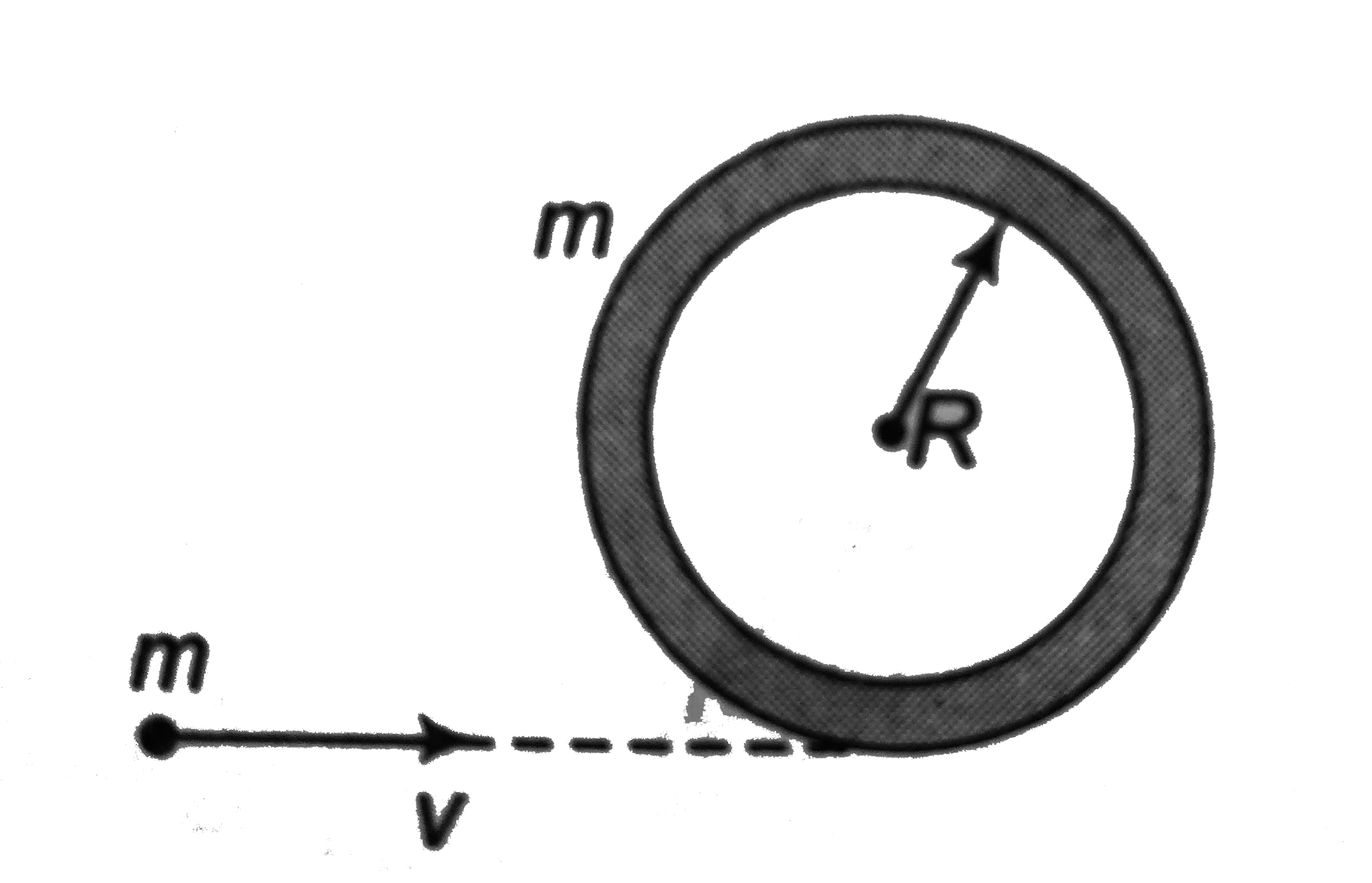
A circular ring of mass m and radius R rests flat on a horizontal smooth surface as shown in figure. A particle of mass m, and moving with a velocity v. Collides inelastically (e=0) with the ring the angular velocity with which the system rotates after the particle strikes the ring is
View SolutionThe moment of inertia of a ring of mass M and radius R about PQ axis will be

View SolutionA ring of mass m and radius R is placed on a rough horizontal surface (co-efficient of friction μ) with velocity of C.M.v0 and angular speed 2V0R as shown in figure. Initially the ring is rolling with slipping but attains pure rolling motion after some time t. Then
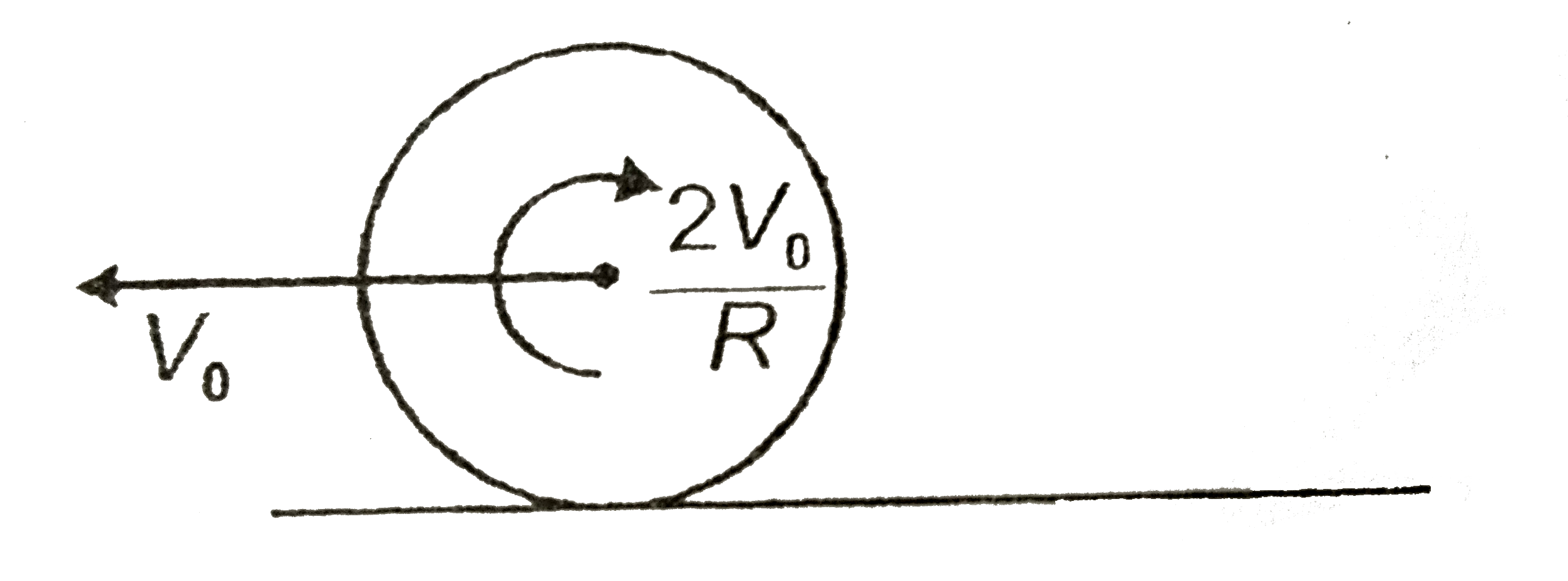
View Solution
