A stone is projected from level ground at t=0 sec such that its horizontal and vertical components of initial velocity are 10ms and 20ms respectively. Then the instant of time at which tangential and normal components of acceleration of stone are same is: (neglect air resistance)g=10ms2.
12sec
32sec
3 sec
4 sec
The correct Answer is:C
To solve the problem, we need to find the instant of time at which the tangential and normal components of acceleration of a stone projected from level ground are the same. The stone is projected with horizontal and vertical components of initial velocity of 10 m/s and 20 m/s, respectively, and we can neglect air resistance with g=10m/s2.
1. Identify the Components of Motion:
- The horizontal component of the initial velocity, ux=10m/s.
- The vertical component of the initial velocity, uy=20m/s.
2. Determine the Time of Flight:
- The total time of flight T for a projectile is given by the formula:
T=2uyg
- Substituting the values:
T=2×2010=4s
3. Tangential and Normal Acceleration:
- The tangential acceleration at is due to the change in the vertical component of velocity, which is influenced by gravity:
at=−g=−10m/s2
- The normal acceleration an is given by:
an=v2R
- In projectile motion, R is the radius of curvature, which can be related to the vertical and horizontal components of velocity.
4. Finding the Velocity Components:
- The horizontal velocity vx remains constant:
vx=10m/s
- The vertical velocity vy at time t is given by:
vy=uy−gt=20−10t
5. Calculate the Magnitude of Velocity:
- The magnitude of the total velocity v is:
v=√v2x+v2y=√(10)2+(20−10t)2
6. Setting Tangential and Normal Acceleration Equal:
- We need to find when at=an:
−10=v2R
- Since R can be considered as the vertical component of velocity divided by the acceleration due to gravity:
R=vyg=20−10t10
- Therefore, we can write:
−10=v220−10t10
- Rearranging gives:
−10⋅20−10t10=v2
7. Substituting the Velocity:
- Substitute v2=102+(20−10t)2:
−10⋅20−10t10=100+(20−10t)2
8. Solving the Equation:
- This leads to a quadratic equation in t. Solving this will yield two values of t:
- One value will be t=1s (when the stone is ascending).
- The other value will be t=3s (when the stone is descending).
9. Conclusion:
- The instant of time at which the tangential and normal components of acceleration are the same is t=3s.
Final Answer:
The instant of time at which the tangential and normal components of acceleration of the stone are the same is 3 seconds.
- The horizontal component of the initial velocity, ux=10m/s.
- The vertical component of the initial velocity, uy=20m/s.
- The total time of flight T for a projectile is given by the formula:
T=2uyg
- Substituting the values:
T=2×2010=4s
- The tangential acceleration at is due to the change in the vertical component of velocity, which is influenced by gravity:
at=−g=−10m/s2
- The normal acceleration an is given by:
an=v2R
- In projectile motion, R is the radius of curvature, which can be related to the vertical and horizontal components of velocity.
- The horizontal velocity vx remains constant:
vx=10m/s
- The vertical velocity vy at time t is given by:
vy=uy−gt=20−10t
- The magnitude of the total velocity v is:
v=√v2x+v2y=√(10)2+(20−10t)2
- We need to find when at=an:
−10=v2R
- Since R can be considered as the vertical component of velocity divided by the acceleration due to gravity:
R=vyg=20−10t10
- Therefore, we can write:
−10=v220−10t10
- Rearranging gives:
−10⋅20−10t10=v2
- Substitute v2=102+(20−10t)2:
−10⋅20−10t10=100+(20−10t)2
- This leads to a quadratic equation in t. Solving this will yield two values of t:
- One value will be t=1s (when the stone is ascending).
- The other value will be t=3s (when the stone is descending).
- The instant of time at which the tangential and normal components of acceleration are the same is t=3s.
The instant of time at which the tangential and normal components of acceleration of the stone are the same is 3 seconds.
Topper's Solved these Questions
Similar Questions
A stone is projectef from level ground such that its horizontal and vertical components of initial velocity are ux=10ms and uy=20ms respectively. Then the angle between velocity vector of stone one second before and one second after it attains maximum height is:
View SolutionA body is projected with an initial velocity of 58.8 m/s at angle 60° with the vertical. The vertical component of velocity after 2 sec is
View SolutionA projectile is fired at an angle of 30∘ to the horizontal such that the vertical component of its initial velocity is 80m/s. Its time of fight is T. Its velocity at t=T/4 has a magnitude of nearly.
View SolutionA particle is projected with velocity 20√2m/s at 45∘ with horizontal. After 1s , find tangential and normal acceleration of the particle. Also, find radius of curvature of the trajectory at that point. (Take g=10m/s2)
View SolutionA body is projected with an initial Velocity 20 m/s at 60° to the horizontal. Its initial velocity vector is- (g=10 m/s2)
View SolutionTwo stones are projected from level ground. Trajectory of two stones are shown in figure. Both stones have same maximum heights above level ground as shown. Let T1 and T2 be their time of flights and u1 and u2 be their speeds of projection respectively (neglect air resistance). then
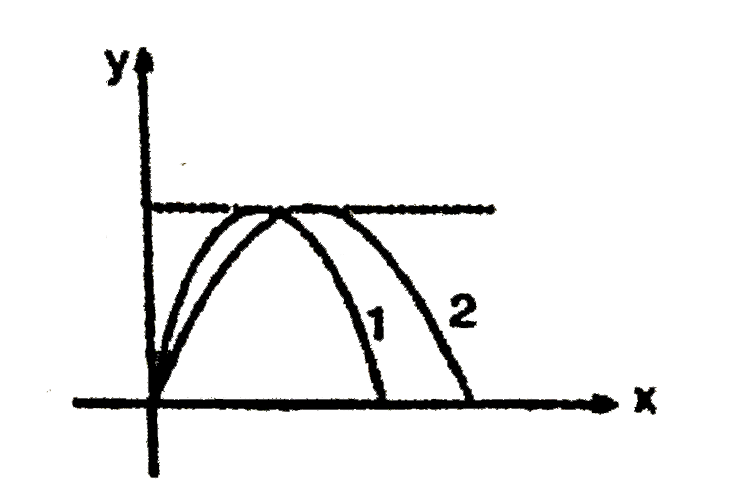
View SolutionA body is thrown into air with a velocity 5 m/s making an angle 30∘ with the horizontal .If the vertical component of the velocity is 5 m/s what is the velocity of the body ? Also find the horizontal component .
View SolutionA stone is dropped from a height 300 m and at the same time another stone is projected vertically upwards with a velocity of 100m/sec. Find when and where the two stones meet.
View SolutionA stone is projected with speed 20m/s at angle 37∘ with the horizontal and it hits the ground with speed 12m/s due to air resistance. Assume the effect of air resistance to reduce only horizontal component of velocity. Then the time of flight will be-
View SolutionA stone is projected from the ground with a velocity of 20 m/s at angle 30∘ with the horizontal. After one second it clears a wall then find height of the wall. (g=10ms−2)
View Solution
