A particle is projected with velocity 20√2m/s at 45∘ with horizontal. After 1s , find tangential and normal acceleration of the particle. Also, find radius of curvature of the trajectory at that point. (Take g=10m/s2)
The correct Answer is:A, B, D
To solve the problem step by step, we will use the following approach:
Step 1: Break down the initial velocity into components
The initial velocity u is given as 20√2m/s at an angle of 45∘ with the horizontal.
- The horizontal component ux is:
ux=ucos(45∘)=20√2⋅1√2=20m/s
- The vertical component uy is:
uy=usin(45∘)=20√2⋅1√2=20m/s
Step 2: Determine the velocity after 1 second
The horizontal velocity remains constant since there is no horizontal acceleration. The vertical velocity changes due to gravity.
- Horizontal velocity vx=ux=20m/s
- Vertical velocity after 1 second:
vy=uy−g⋅t=20−10⋅1=10m/s
Step 3: Calculate the total velocity after 1 second
The total velocity v can be calculated using the Pythagorean theorem:
v=√v2x+v2y=√(20)2+(10)2=√400+100=√500=10√5m/s
Step 4: Calculate the tangential acceleration
The tangential acceleration at is due to the change in the vertical component of the velocity. Since the only acceleration acting on the particle is gravity, the tangential acceleration is:
at=−g=−10m/s2
Step 5: Calculate the normal acceleration
The normal acceleration an can be calculated using the formula:
an=v2R
where R is the radius of curvature. We will first find the radius of curvature in the next step.
Step 6: Calculate the radius of curvature
The radius of curvature R can be calculated using the formula:
R=v2g=(10√5)210=50010=50m
Step 7: Calculate the normal acceleration using the radius of curvature
Now we can find the normal acceleration:
an=v2R=(10√5)250=50050=10m/s2
Final Results
- Tangential acceleration at=−10m/s2
- Normal acceleration an=10m/s2
- Radius of curvature R=50m
The initial velocity u is given as 20√2m/s at an angle of 45∘ with the horizontal.
ux=ucos(45∘)=20√2⋅1√2=20m/s
uy=usin(45∘)=20√2⋅1√2=20m/s
The horizontal velocity remains constant since there is no horizontal acceleration. The vertical velocity changes due to gravity.
vy=uy−g⋅t=20−10⋅1=10m/s
The total velocity v can be calculated using the Pythagorean theorem:
v=√v2x+v2y=√(20)2+(10)2=√400+100=√500=10√5m/s
The tangential acceleration at is due to the change in the vertical component of the velocity. Since the only acceleration acting on the particle is gravity, the tangential acceleration is:
at=−g=−10m/s2
The normal acceleration an can be calculated using the formula:
an=v2R
where R is the radius of curvature. We will first find the radius of curvature in the next step.
The radius of curvature R can be calculated using the formula:
R=v2g=(10√5)210=50010=50m
Now we can find the normal acceleration:
an=v2R=(10√5)250=50050=10m/s2
- Tangential acceleration at=−10m/s2
- Normal acceleration an=10m/s2
- Radius of curvature R=50m
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Subjective Questions
2 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - JEE Main
23 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Level 2 Comprehension Based
5 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
A particle is projected from ground with velocity 40√2m/s at 45∘. At time t=2s
View SolutionA particle is projected with velocity of 10ms at an angle of 15° with horizontal.The horizontal range will be(g=10ms2)
View SolutionA particle is projected at t=0 with velocity u at angle θ with the horizontal. Then the ratio of the tangential acceleration and the radius of curvature at the point of projection is :
View SolutionA particle is projected with speed 20ms−1 at an angle 30∘ With horizontal. After how much time the angle between velocity and acceleration will be 90∘
View SolutionA particle is projected from ground with velocity 40(√2)m/s at 45∘. Find
(a) velocity and
(b) displacement of the particle after 2 s. (g=10m/s2)
View SolutionA particle of mass m=1kg is projected with speed u=20√2m/s at angle θ=45∘ with horizontal find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
View SolutionThe particle of mass 1 kg is projected with velocity 20√2m/s at 45∘ with ground . When , the particle is at highest point (g=10m/s2),
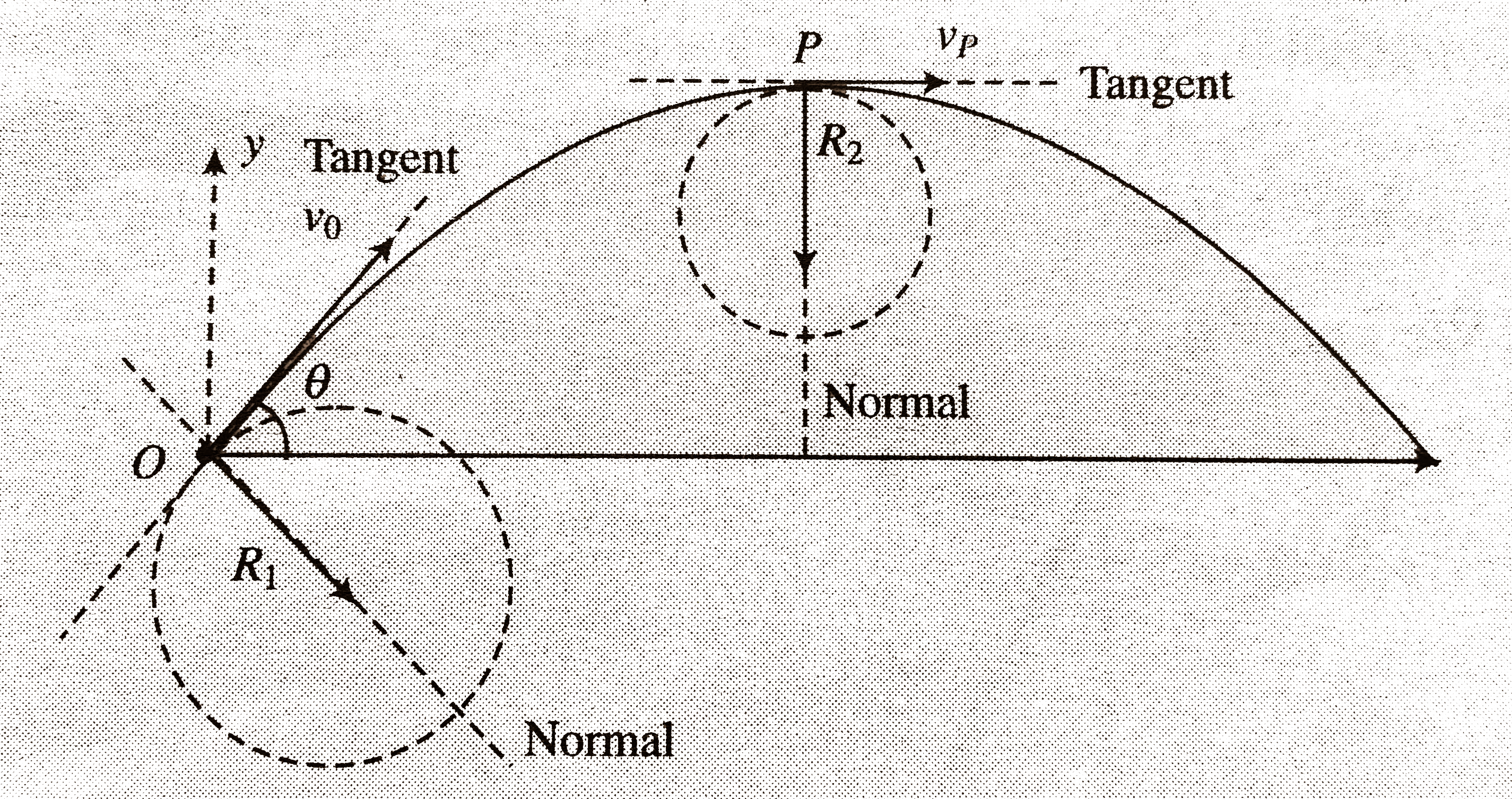
View SolutionA particle is projected at angle θ with horizontal with velocity v0att=0. Find
(a) tangential and normal acceleration of the particle at t=0 and at highest point of its trajectory.
(b) the radius of curvature a=0 and highest point.
 .
.
View SolutionA particle is projected with a velocity 10 m//s at an angle 37∘ to the horizontal. Find the location at which the particle is at a height 1 m from point of projection.
View SolutionA stone is thrown horizontally with a velocity of 10m/sec. Find the radius of curvature of it’s trajectory at the end of 3s after motion began. (g=10m/s2)
View Solution
